初中北师大版2 二次函数的图像与性质优秀ppt课件

这是一份初中北师大版2 二次函数的图像与性质优秀ppt课件，共12页。PPT课件主要包含了直线和圆相交，直线和圆相切，直线和圆相离，直线何时变为切线，切线的判定，切线判定的应用，三角形与圆的位置关系，挑战自我等内容，欢迎下载使用。

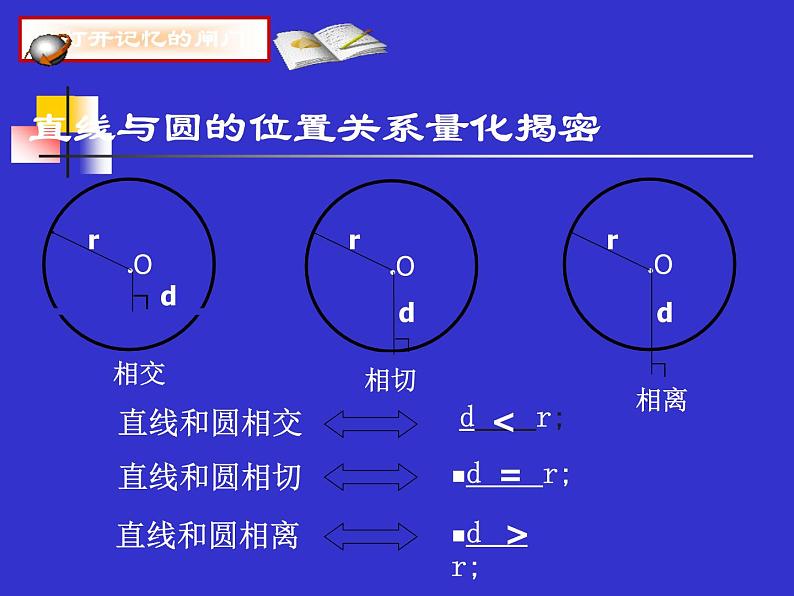
直线与圆的位置关系量化揭密
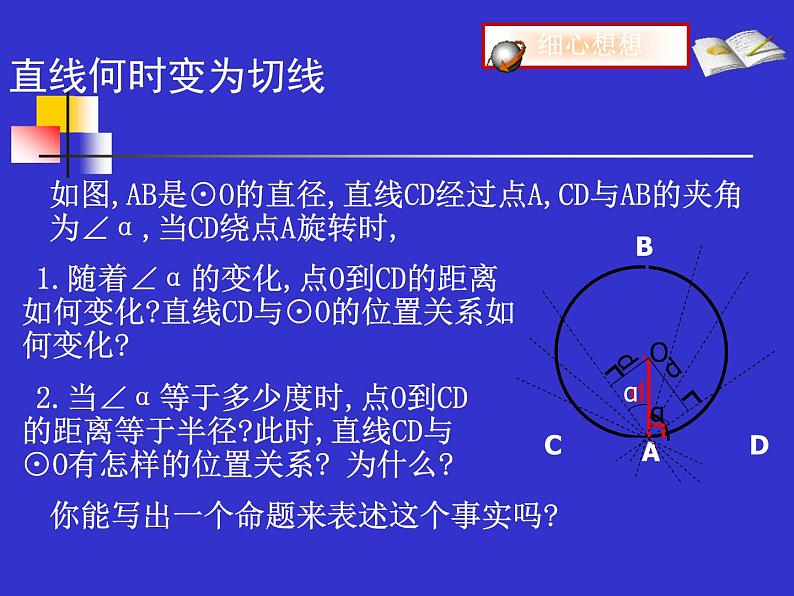
如图,AB是⊙O的直径,直线CD经过点A,CD与AB的夹角为∠α,当CD绕点A旋转时,
你能写出一个命题来表述这个事实吗?
1.随着∠α的变化,点O到CD的距离如何变化?直线CD与⊙O的位置关系如何变化?
2.当∠α等于多少度时,点O到CD的距离等于半径?此时,直线CD与⊙O有怎样的位置关系? 为什么?
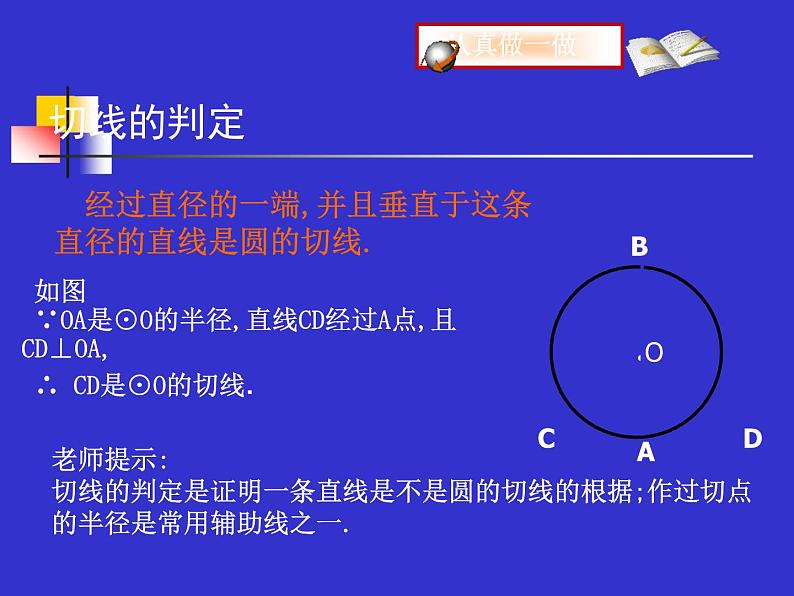
经过直径的一端,并且垂直于这条直径的直线是圆的切线.
老师提示:切线的判定是证明一条直线是不是圆的切线的根据;作过切点的半径是常用辅助线之一.
如图∵OA是⊙O的半径,直线CD经过A点,且CD⊥OA,∴ CD是⊙O的切线.
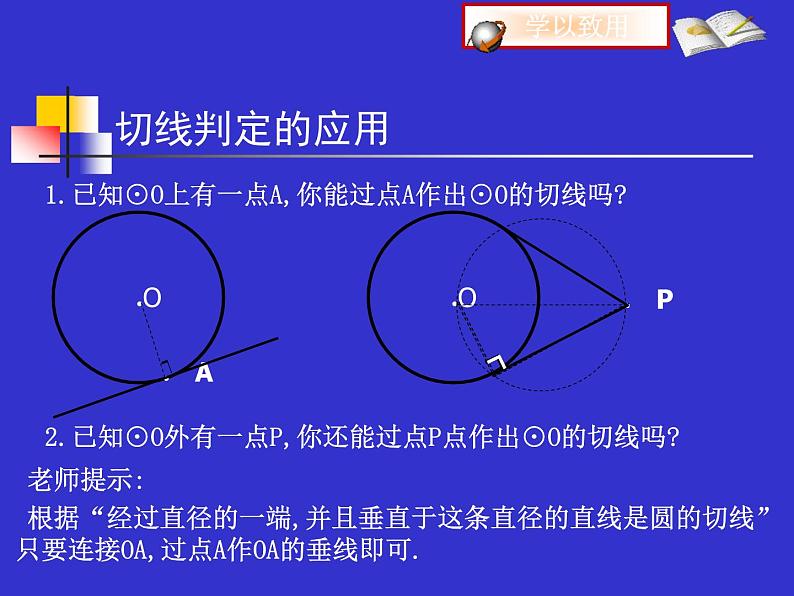
1.已知⊙O上有一点A,你能过点A作出⊙O的切线吗?
老师提示:根据“经过直径的一端,并且垂直于这条直径的直线是圆的切线”只要连接OA,过点A作OA的垂线即可.
2.已知⊙O外有一点P,你还能过点P点作出⊙O的切线吗?
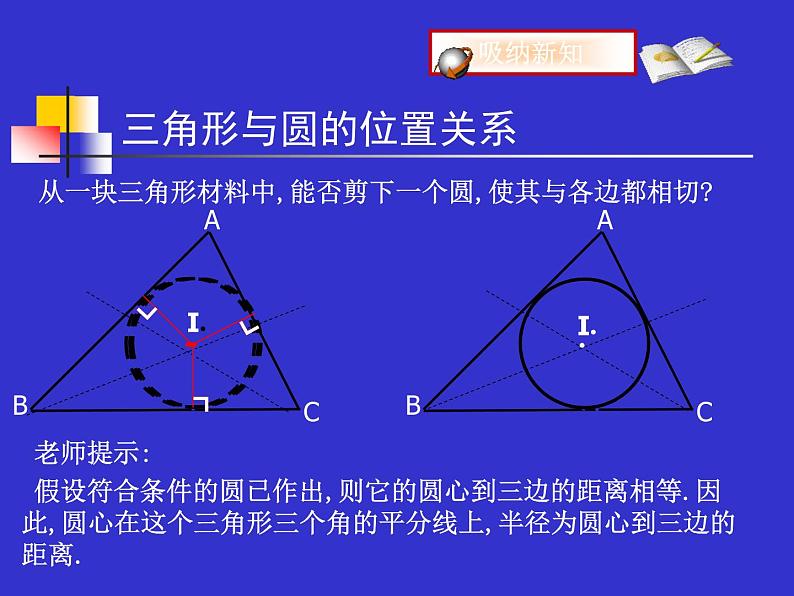
从一块三角形材料中,能否剪下一个圆,使其与各边都相切?
老师提示:假设符合条件的圆已作出,则它的圆心到三边的距离相等.因此,圆心在这个三角形三个角的平分线上,半径为圆心到三边的距离.
这样的圆可以作出几个?为什么?
∵直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),
∴和△ABC三边都相切的圆可以作出一个,并且只能作一个.
这圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
如图，AB是⊙O的直径，∠ABT=45°，AT＝AB．求证：AT是⊙O的切线．
分析：AT经过直径的一端，因此只要证AT垂直于AB即可，而由已知条件可知AT=AB，所以∠ABT＝∠ATB，又由∠ABT＝45°，所以∠ATB=45°． 由三角形内角和可证∠TAB=90°，即AT⊥AB．
三角形与圆的“切”关系
1.以边长为3,4,5的三角形的三个顶点为圆心,分别作圆与对边相切,则这三个圆的半径分别是多少?.
2.分别作出锐角三角形、直角三角形、钝角三角形的内切圆,并说明它们内心的位置情况.
老师提示:先确定圆心和半径,尺规作图要保留作图痕迹.
必做 :习题3.8 1,2题 选做 已知AB是⊙O的直径，BC是⊙O的切线，切点为B，OC平行于弦AD． 求证：DC是⊙O的切线．