
北师大版九年级下册第三章 圆7 切线长定理完美版课件ppt
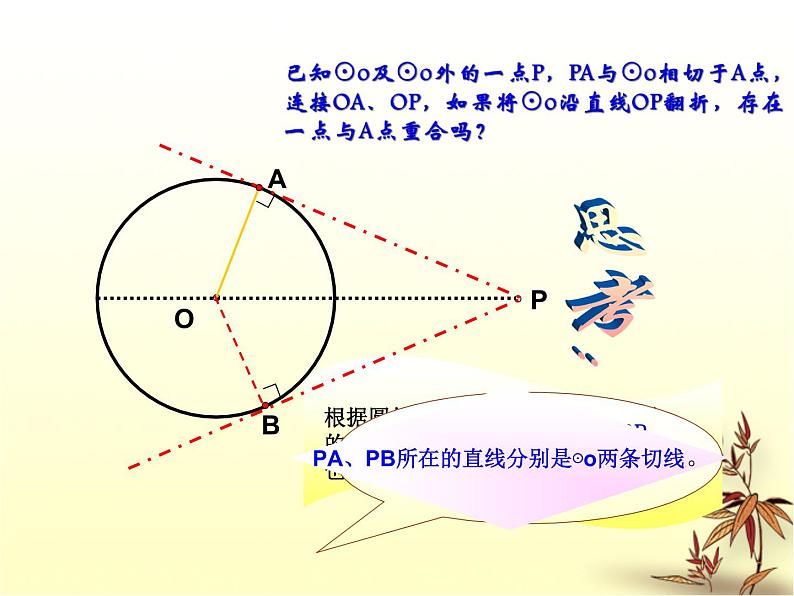
展开你能发现OA与PA,OB与PB之间的关系吗?
PA、PB所在的直线分别是⊙两条切线。
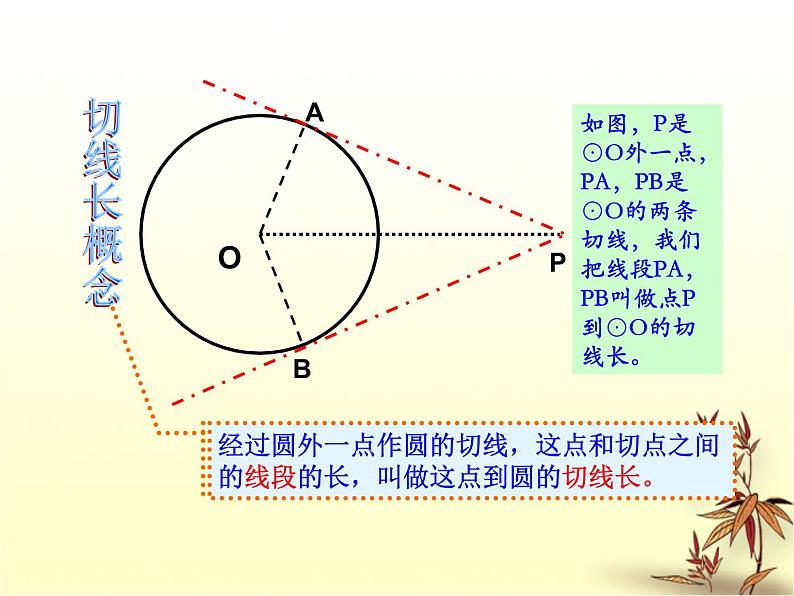
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长。
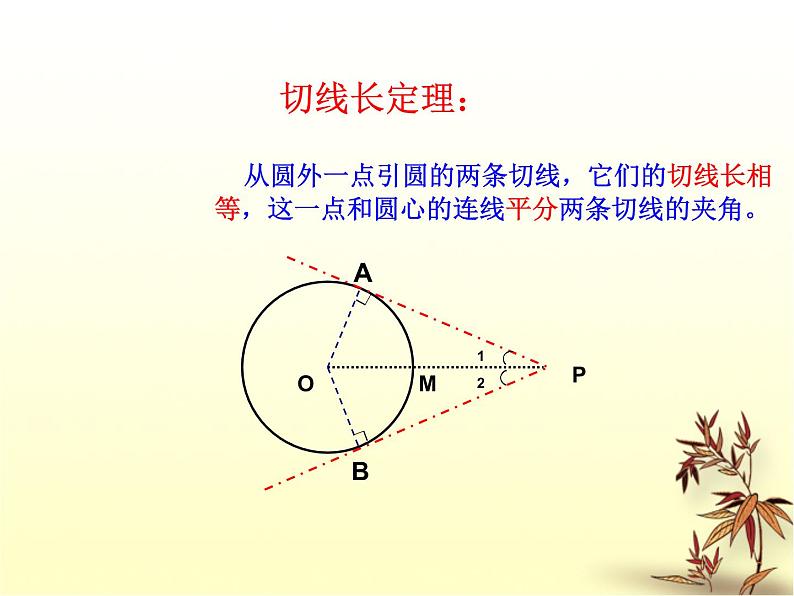
如图,P是⊙O外一点,PA,PB是⊙O的两条切线,我们把线段PA,PB叫做点P到⊙O的切线长。
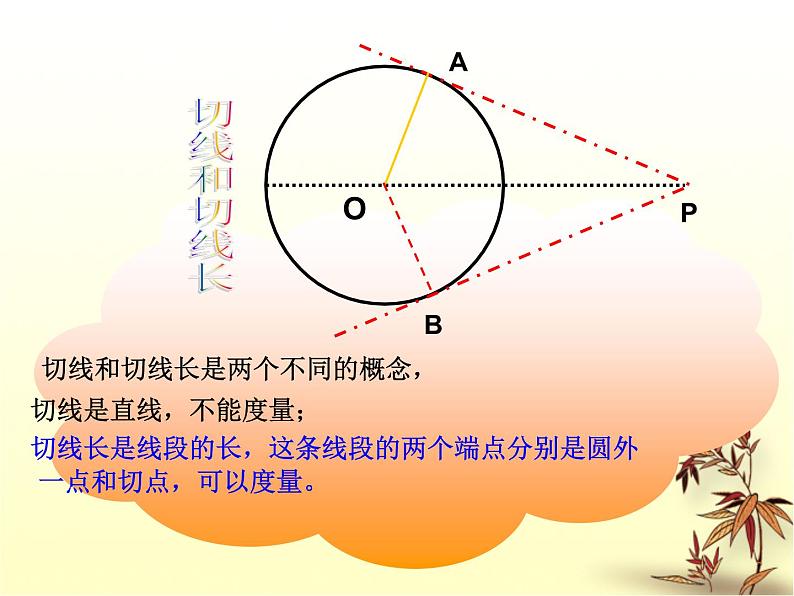
切线和切线长是两个不同的概念, 切线是直线,不能度量; 切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。
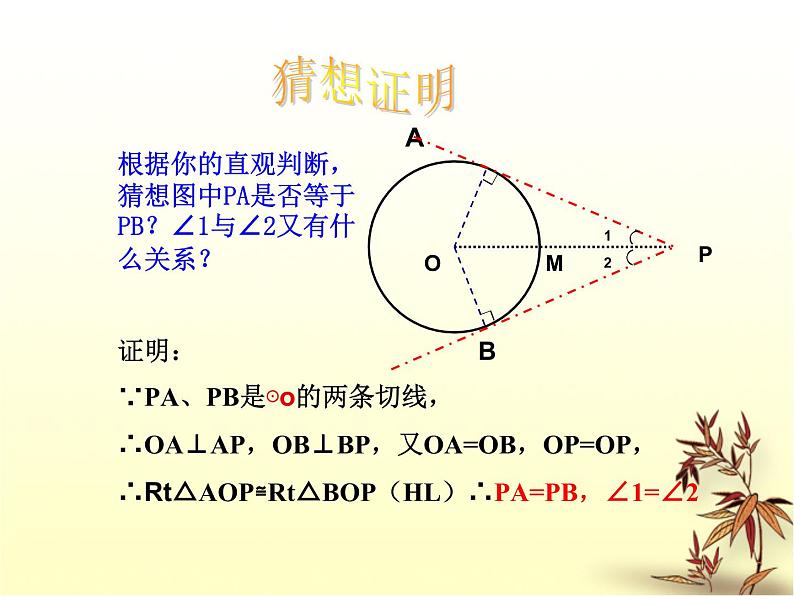
根据你的直观判断,猜想图中PA是否等于PB?∠1与∠2又有什么关系?
证明:∵PA、PB是⊙的两条切线,∴OA⊥AP,OB⊥BP,又OA=OB,OP=OP,∴Rt△AOP≌Rt△BOP(HL)∴PA=PB,∠1=∠2
从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。
已知:⊙O的半径为3厘米,点P和圆心O的距离为6厘米,经过点P和⊙O的两条切线,求这两条切线的夹角及切线长.
李师傅在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,且使圆的面积最大。下图是他的几种设计,请同学们帮他确定一下。
1、定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形。
2、性质: 内心到三角形三边的距离相等; 内心与顶点连线平分内角。
作三角形内切圆的方法:
1、作∠B、∠C的平分线BM和CN,交点为I。
2.过点I作ID⊥BC,垂足为D。
3.以I为圆心,ID为半径作⊙I. ⊙I就是所求的圆。
例1:已知:在△ABC中,BC=9cm,AC=14cm,AB=13cm,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长。
解:因为△ABC的内切圆分别和BC、AC、AB切于点D、E、F,由切线长定理知
AE=AF,CE=CD,BD=BF
∴AF+BD+CE= (AB+AC+BC)
∴BD=AB-AF=13-9=4
∴CE=BC-BD=9-4=5
(1)∵点O是△ABC的内心,
∴ ∠BOC=180 °-(∠1+ ∠3)
= 180 °-(25°+ 35 °)
例2 如图,在△ABC中,点O是内心, 若∠ABC=50°, ∠ACB=70°,求∠BOC的度数
初中数学北师大版九年级下册7 切线长定理评课ppt课件: 这是一份初中数学北师大版九年级下册7 切线长定理评课ppt课件,共16页。PPT课件主要包含了情境引入,探究新知,知识拓展,定理应用,巩固练习,师生小结,布置作业等内容,欢迎下载使用。
初中数学北师大版九年级下册7 切线长定理教学ppt课件: 这是一份初中数学北师大版九年级下册7 切线长定理教学ppt课件,文件包含北师大版初中数学九年级下册37切线长定理同步课件pptx、北师大版初中数学九年级下册37切线长定理教学设计含教学反思docx等2份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
初中数学北师大版九年级下册第三章 圆7 切线长定理课文内容ppt课件: 这是一份初中数学北师大版九年级下册第三章 圆7 切线长定理课文内容ppt课件,文件包含37切线长定理pptx、37切线长定理doc等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。













