北师大版九年级下册5 确定圆的条件获奖课件ppt

这是一份北师大版九年级下册5 确定圆的条件获奖课件ppt，共24页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，你怎样画这个圆等内容，欢迎下载使用。

1.确定圆的条件 2.三角形的外接圆与外心. （重点、难点）
1、过一点可以作几条直线？
2、过几点可确定一条直线？
3、过几点可以确定一个圆呢？
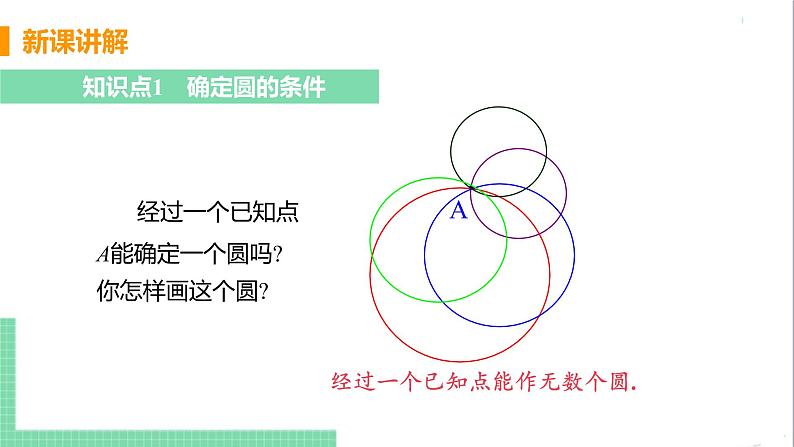
知识点1 确定圆的条件
经过一个已知点A能确定一个圆吗?
经过一个已知点能作无数个圆.
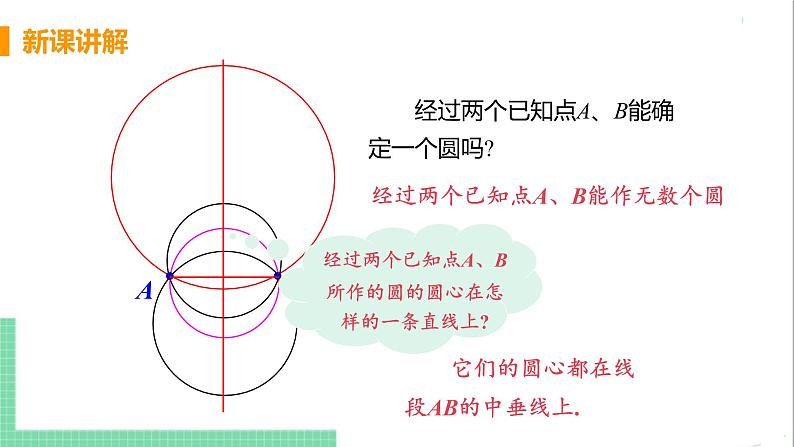
经过两个已知点A、B能确定一个圆吗?
经过两个已知点A、B能作无数个圆
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上?
它们的圆心都在线段AB的中垂线上.
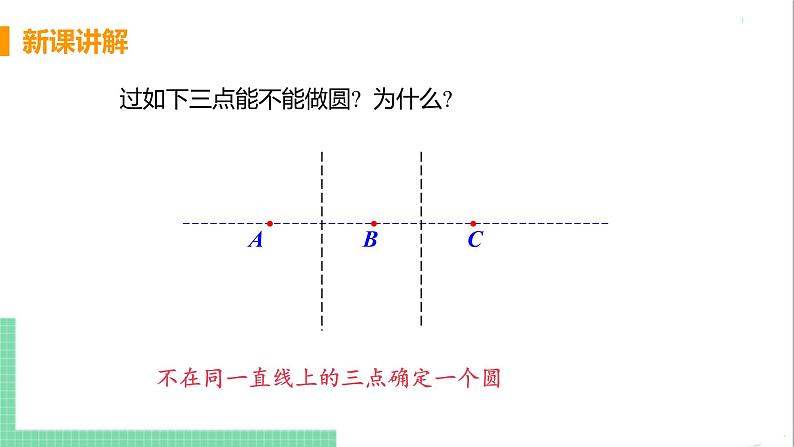
过如下三点能不能做圆? 为什么?
不在同一直线上的三点确定一个圆
如图所示，点A，B，C 在同一条直线上，点D 在直线AB 外，过这四个点中的任意三个点，能画圆的个数是（ ）A.1 B.2 C.3 D.4
（1）四个点中取三个点的组数；（2）去掉三点共线的组数.
过不在同一条直线上的三点确定一个圆，在点A，B，C，D 四个点中取三个点的方法有：点A，B，C；点A，B，D；点B，C，D；点A，C，D，共四组. 又因A，B，C 三点在同一条直线上，故过这四个点中的任意三个点能画圆的个数为3.
如图，在5×5的正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是(　　)A．点P B．点Q C．点R D．点M
知识点2 三角形的外接圆与外心
已知△ABC，用直尺和圆规作出过点A、B、C的圆.
经过三角形各个顶点的圆叫做三角形的外接圆，外接圆的圆心叫做三角形的外心，这个三角形叫做圆的内接三角形.
如图：⊙O是△ABC的外接圆， △ABC是⊙O的内接三角形，点O是△ABC的外心.
外心是△ABC三条边的垂直平分线的交点，它到三角形的三个顶点的距离相等.
三角形外接圆的作法：(1)作三角形任意两边的垂直平分线，确定其交点；(2)以该交点为圆心，以交点到三个顶点中任意一 点的距离为半径作圆即可．
求三角形的外接圆半径的方法：求三角形的外接圆半径时, 最常用的方法是作出圆心与三角形顶点的连线( 即半径)，或延长使这条半径变为直径, 将求半径转化为直角三角形中求边的长.
如图所示，△ ABC 内接于⊙ O，∠ C=45 °，AB=4，求⊙ O 的半径.
要求⊙O的半径，已知弦AB的长，需以AB为边与⊙O的半径(或直径)构成等腰直角三角形，因此有两个切入点．方法一：如图2，连接OA，OB，利用圆周角定理可得∠AOB＝2∠C＝90°，再利用勾股定理求出半径；方法二：如图2，作直径AD，连接BD，利用同弧所对的圆周角相等，得∠D＝∠C＝45°，再利用勾股定理可求出半径．
方法一：如图1，连接OA，OB，设⊙O的半径为r，∵∠C＝45°，∴∠AOB＝2∠C＝90°.∴OA2＋OB2＝AB2，即r2＋r2＝42. 解得r1＝2 ，r2＝－2 (不符合题意，舍去)．∴⊙O的半径为2 .
方法二：如图2，作直径AD，连接BD，设⊙O的半径为r.∵AD为⊙O的直径，∴∠ABD＝90°.又∵∠D＝∠C＝45°，∴∠DAB＝45°.∴BD＝AB＝4.在Rt△ABD中，AB2＋BD2＝AD2，即42＋42＝(2r)2解得r1＝2 ，r2＝－2 (不符合题意，舍去)．∴⊙O的半径为2 .
已知下面的三个三角形，分别作出它们的外接圆. 它们外心的位置有怎样的特点？
解：作图略．经观察发现：锐角三角形的外心在三 角形的内部；直角三角形的外心在斜边的中点 处；钝角三角形的外心在三角形的外部．　
(1)只有确定了圆心和圆的半径，这个圆的位置和大小 才唯一确定.
(2)经过一个已知点能作无数个圆.
(3)经过两个已知点A、B能作无数个圆！这些圆的圆 心在线段AB的垂直平分线上.
(4)不在同一直线上的三个点确定一个圆.
(5)外接圆，外心的概念.
1.下列说法中正确的是(　　)A．两个点确定一个圆B．三个点确定一个圆C．四个点确定一个圆D．不共线的三个点确定一个圆
2.如图，在平面直角坐标系xOy中，点A的坐标为(0，3)，点B的坐标为(2，1)，点C的坐标为(2，－3)，则经画图操作可知△ABC的外心坐标应是(　　)A．(0，0) B．(1，0) C．(－2，－1) D．(2，0)