人教A版 (2019)必修 第二册8.4 空间点、直线、平面之间的位置关系精品同步练习题

8.6　空间直线、平面的垂直

8.6.1　直线与直线垂直

课后篇巩固提升

基础巩固

1.

如图,在三棱锥D-ABC中,AC=BD,且AC⊥BD,E,F分别是棱DC,AB的中点,则EF和AC所成的角等于(　　)

A.30°

B.45°

C.60°

D.90°

答案B

解析如图所示,取BC的中点G,连接FG,EG.

∵E,F分别为CD,AB的中点,∴FG∥AC,EG∥BD,

且FG=AC,EG=BD.

∵AC=BD,∴FG=EG,

∴∠EFG为EF与AC所成的角或其补角.

∵AC⊥BD,∴FG⊥EG,∴∠FGE=90°,

∴△EFG为等腰直角三角形.

∴∠EFG=45°,即EF与AC所成的角为45°.

2.若∠AOB=120°,直线a∥OA,a与OB为异面直线,则a和OB所成的角的大小为　　　　　. 

答案60°

解析∵a∥OA,根据等角定理,又异面直线所成的角为锐角或直角,∴a与OB所成的角为60°.

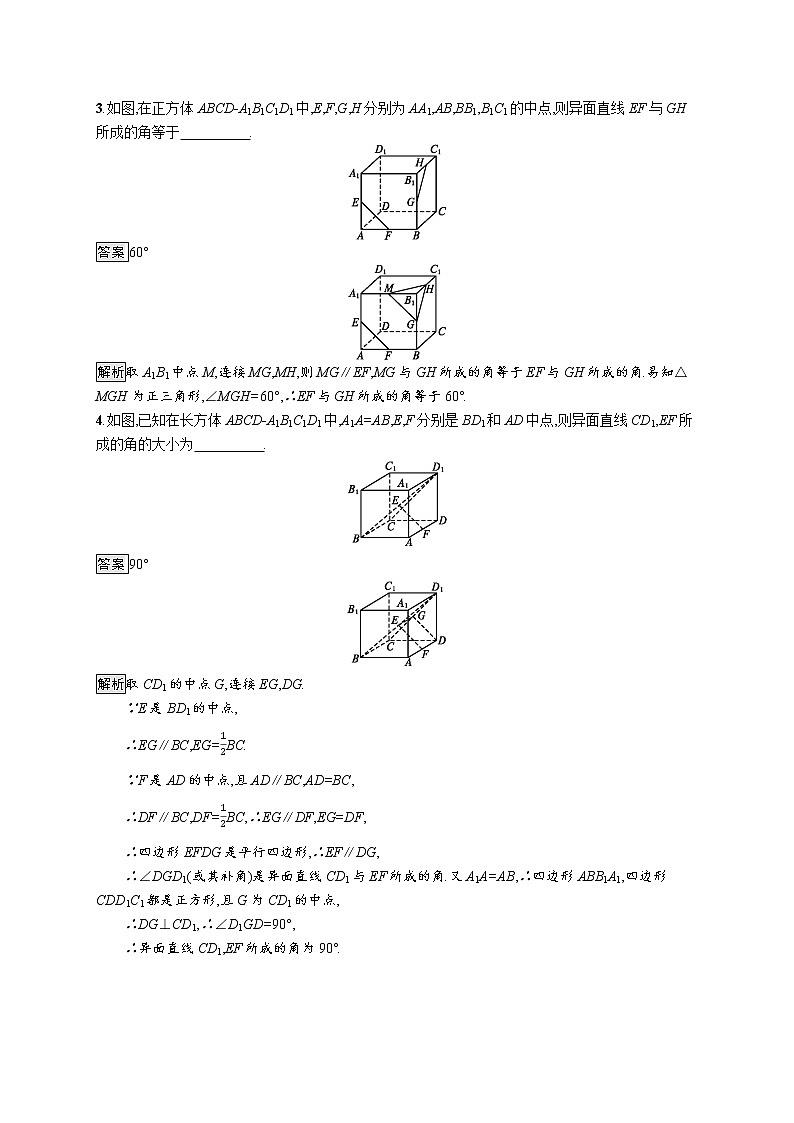
3.如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为AA1,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于　　　　　. 

答案60°

解析取A1B1中点M,连接MG,MH,则MG∥EF,MG与GH所成的角等于EF与GH所成的角.易知△MGH为正三角形,∠MGH=60°,∴EF与GH所成的角等于60°.

4.如图,已知在长方体ABCD-A1B1C1D1中,A1A=AB,E,F分别是BD1和AD中点,则异面直线CD1,EF所成的角的大小为　　　　　. 

答案90°

解析取CD1的中点G,连接EG,DG.

∵E是BD1的中点,

∴EG∥BC,EG=BC.

∵F是AD的中点,且AD∥BC,AD=BC,

∴DF∥BC,DF=BC,∴EG∥DF,EG=DF,

∴四边形EFDG是平行四边形,∴EF∥DG,

∴∠DGD1(或其补角)是异面直线CD1与EF所成的角.又A1A=AB,∴四边形ABB1A1,四边形CDD1C1都是正方形,且G为CD1的中点,

∴DG⊥CD1,∴∠D1GD=90°,

∴异面直线CD1,EF所成的角为90°.

5.如图所示,在空间四边形ABCD中,AB=CD,且AB与CD所成的角为30°,E,F分别为BC,AD的中点,则EF与AB所成角的大小为　　　　. 

答案15°或75°

解析取AC的中点G,连接EG,FG,则EG∥AB,且EG=AB

,FG∥CD,且FG=CD,由AB=CD知EG=FG.

易知∠GEF(或它的补角)为EF与AB所成的角,∠EGF(或它的补角)为AB与CD所成的角.

∵AB与CD所成的角为30°,∴∠EGF=30°或150°.

由EG=FG知△EFG为等腰三角形,

当∠EGF=30°时,∠GEF=75°;

当∠EGF=150°时,∠GEF=15°.

故EF与AB所成的角为15°或75°.

6.在空间四边形ABCD中,两条对边AB=CD=3,E,F分别是另外两条对边AD,BC上的点,且,EF=,求AB和CD所成角的大小.

解如图,连接BD,过点E作AB的平行线交BD于点O,连接OF.∵EO∥AB,∴.

∵AB=3,∴EO=2.又,∴,

∴OF∥DC,∴OE与OF所成的角即为AB和CD所成的角,.∵DC=3,∴OF=1.在△OEF中,OE2+OF2=5,EF2=()2=5,∴OE2+OF2=EF2,

∴∠EOF=90°,所以AB和CD所成的角为90°.

能力提升

1.如图,在四棱柱ABCD-A1B1C1D1中,侧面都是矩形,底面四边形ABCD是菱形且AB=BC=2,∠ABC=120°,若异面直线A1B和AD1所成的角为90°,试求AA1的长.

解连接CD1,AC.

由题意得四棱柱ABCD-A1B1C1D1中,A1D1∥BC,A1D1=BC,∴四边形A1BCD1是平行四边形,∴A1B∥CD1,∴∠AD1C(或其补角)为A1B和AD1所成的角.∵异面直线A1B和AD1所成的角为90°,∴∠AD1C=90°.∵四棱柱ABCD-A1B1C1D1中,AB=BC=2,∴△ACD1是等腰直角三角形,∴AD1=AC.∵底面四边形ABCD是菱形,且AB=BC=2,∠ABC=120°,

∴AC=2×sin 60°×2=6,AD1=AC=3,

∴AA1=.

2.

如图,空间四边形ABCD的对棱AD,BC成60°的角,且AD=BC=a,平行于AD与BC的截面分别交AB,AC,CD,BD于点E,F,G,H.E在AB的何处时截面EGFH的面积最大?最大面积是多少?

解∵AD与BC成60°角,∴∠HGF=60°或120°.

设AE∶AB=x,则=x.又BC=a,

∴EF=ax.由=1-x,得EH=a(1-x).

∴S四边形EFGH=EF×EH×sin 60°=ax×a(1-x)×a2(-x2+x)=a2.

当x=时,S最大值=a2,即当E为AB的中点时,截面的面积最大,最大面积为a2.