



数学第二十七章 相似综合与测试一等奖复习ppt课件
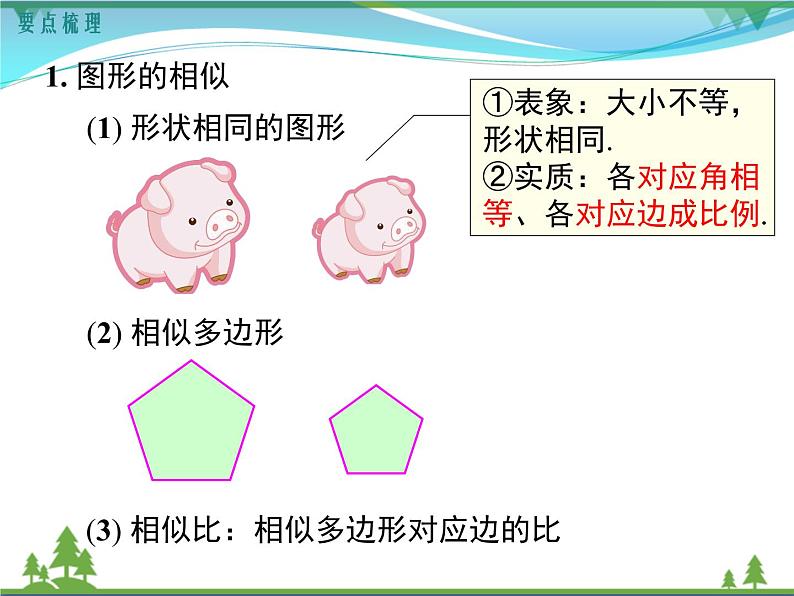
展开(1) 形状相同的图形
(3) 相似比:相似多边形对应边的比
◑通过定义◑平行于三角形一边的直线◑三边成比例◑两边成比例且夹角相等◑两角分别相等◑两直角三角形的斜边和一条直角边成比例
(三个角分别相等,三条边成比例)
2. 相似三角形的判定
◑对应角相等、对应边成比例◑对应高、中线、角平分线的比等于相似比◑周长比等于相似比◑面积比等于相似比的平方
3. 相似三角形的性质
测量不能到达两点间的距离,常构造相似三角形求解.
(不能直接使用皮尺或刻度尺量的)
(不能直接测量的两点间的距离)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决.
4. 相似三角形的应用
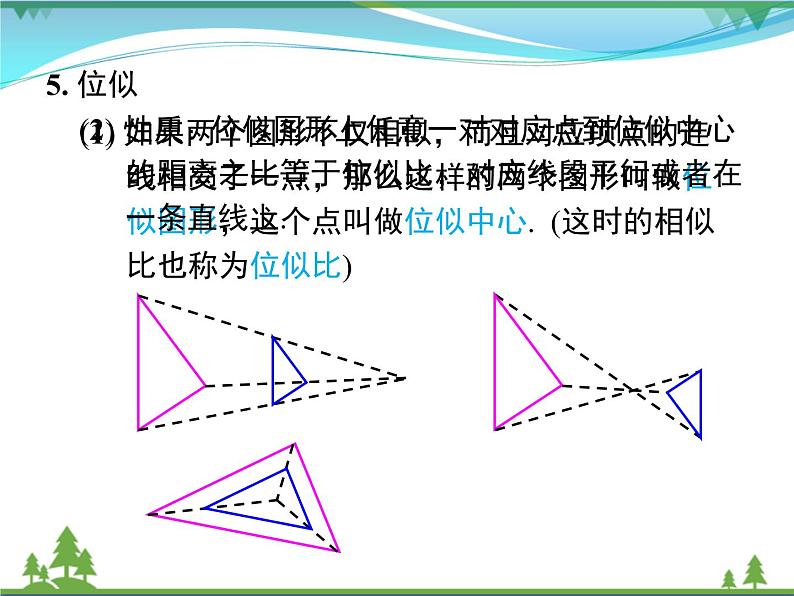
(1) 如果两个图形不仅相似,而且对应顶点的连 线相交于一点,那么这样的两个图形叫做位 似图形,这个点叫做位似中心. (这时的相似 比也称为位似比)
(2) 性质:位似图形上任意一对对应点到位似中心 的距离之比等于位似比;对应线段平行或者在 一条直线上.
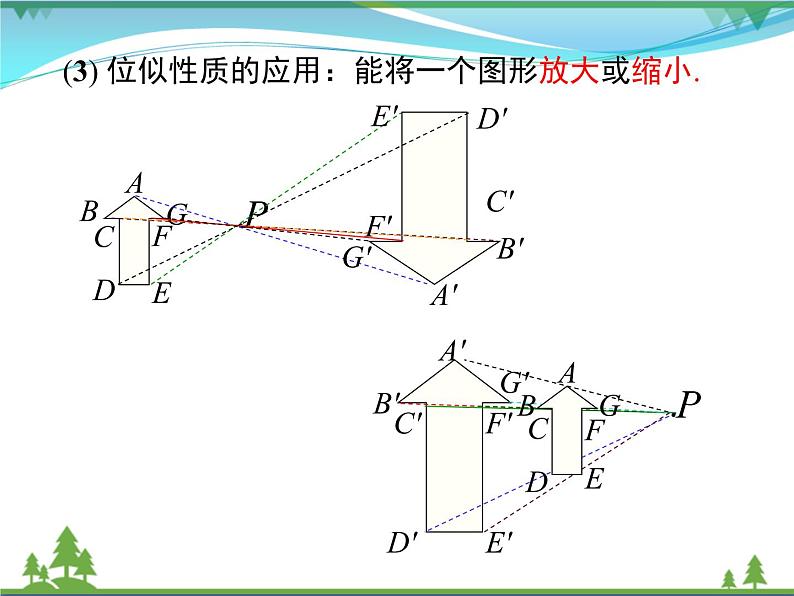
(3) 位似性质的应用:能将一个图形放大或缩小.
(4) 平面直角坐标系中的位似
当位似图形在原点同侧时,其对应顶点的坐标的比为 k;当位似图形在原点两侧时,对应顶点的坐标的比为-k.
位似中的相似比,一般指新图形与原图形的比
例1 如图,当满足下列条件之一时,都可判定 △ADC ∽△ACB.(1) ; (2) ;(3) .
例2 如图,△ABC 中,AB=9,AC=6,点 E 在 AB 上且 AE=3,点 F 在 AC 上,连接 EF,若 △AEF与 △ABC 相似,则 AF = .
【分析】从题干分析△AEF与△ABC相似,此时对应关系不明确,需分类讨论
解析:当△AEF∽△ABC时,AE:AB=AF:AC,即3:9=AF:6,解得AF=2;当△AFE∽△ABC时,AF:AB=AE:AC,即AF:9=3:6,解得AF=4.5;综上所述AF=2 或 4.5.
例3 如图,在 □ABCD 中,点 E 在边 BC 上,BE : EC =1 : 2,连接 AE 交 BD 于点 F,则 △BFE 的面积与 △DFA 的面积之比为 .
【变式题】如图,在 □ABCD 中,点 E 在边 BC 上,EF : AF =1 : 3,连接 AE 交 BD 于点 F,则 △EFB的面积与 △ABD 的面积之比为 .
【注意】求面积比时,要注意相似三角形、等高三角形的区别
解析:∵AD∥BC,∴△EFB∽△AFD,相似比为1:3,∴S△EFB:S△AFD=1:9,∵△EFB与△ABF同高,∴S△EFB:S△ABF=1:3,∴S△EFB:S△ABD=1:12.
证明:∵△ABC是等边三角形, ∴∠BAC=∠ACB=60°, ∠ACF=120°. ∵CE是外角平分线, ∴∠ACE=60°, ∴∠BAC=∠ACE. 又∵∠ADB=∠CDE, ∴△ABD∽△CED.
例4 如图,△ABC 是等边三角形,CE 是外角平分线,点 D 在 AC 上,连接 BD 并延长与 CE 交于点 E.(1) 求证:△ABD ∽△CED;
(2) 若 AB = 6,AD = 2CD,求 BE 的长.
解:作 BM⊥AC 于点 M. ∵ AC=AB=6, ∴ AM=CM=3. ∵ AD = 2CD, ∴CD=2,AD=4, MD=1.
由(1) △ABD ∽△CED得,
例5 如图,CD 是 ⊙O 的弦,AB 是直径,CD⊥AB,垂足为 P,求证:PC2 = PA · PB.
证明:连接AC,BC.
∵AB是直径,∴∠ACB=90°,∴ ∠A + ∠B = 90°.又 ∵CD⊥AB,∴∠CPB=90°,∠PCB+∠B=90°.∴ ∠A=∠CPB,∴ △APC ∽△CPB.
∴ PC2 = AP · PB.
例6 下列四个图形中,位似图形的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
已知 △ABC ∽ △A′B′C′,下列图形中, △ABC 和△A′B′C′ 不存在位似关系的是 ( )
例7 如图,下面的网格中,每个小正方形的边长均为 1,点 O 和 △ABC 的顶点均为小正方形的顶点.
(1) 在图中 △ABC 内部作 △A′B′C′,使 △A′B′C′ 和 △ABC 位似,且位似中心为点 O,位似比为 2 : 3.
(2) 线段 AA′ 的长度是 .
如图,△ABC 在方格纸中. (1) 请在方格纸上建立平面直角坐标系,使A (2,3), C (6,2),并求出 B 点坐标;
解:如图所示, B (2,1).
(2) 以原点 O 为位似中心,位似比为 2,在第一象限内 将 △ABC 放大,画出放大后的图形 △A′B′C′;
解:如图所示.
(3) 计算△A′B′C′的面积 S.
例8 如图,某一时刻小树AB的影子顶端与大树CD的刚好重合.已知小树AB高2.4米,大树CD高5米,而大树的影长为2.5米,求小树与大树之间的距离BD.
解:由题知△ABE∽△CDE,∴AB:CD=BE:DE,即2.4:5=BE:2.5,解得BE=1.2,∴BD=2.5-1.2=1.3(米).
如图,某一时刻一根 2 m 长的竹竿 EF 的影长 GE 为 1.2 m,此时,小红测得一棵被风吹斜的柏树与地面成 30°角,树顶端 B 在地面上的影子点 D 与 B 到垂直地面的落点 C 的距离是 3.6 m,求树 AB的长.
【注意】太阳光线是平行的
解:如图,CD=3.6m,∵△BDC∽△FGE,
∴ BC=6m.在 Rt△ABC 中,∵ ∠A=30°,∴ AB=2BC=12 m,即树长 AB 是 12 m.
例9 星期天,小丽和同学们在碧沙岗公园游玩,他们来到 1928 年冯玉祥将军为纪念北伐军阵亡将士所立的纪念碑前,小丽问:“这个纪念碑有多高呢?”请你利用初中数学知识,结合光的反射原理,设计一种方案测量纪念碑的高度 (画出示意图),并说明理由.
解:如图,线段 AB 为纪念碑,在地面上平放一面镜 子 E,人退后到 D 处,在镜子里恰好看见纪念碑 顶 A. 若人眼距地面距离为 CD,测量出 CD、DE、 BE的长,就可算出纪念碑 AB 的高.
理由:测量出CD、DE、BE的长,因为∠CED=∠AEB,∠D=∠B=90°,易得△ABE∽△CDE.
如图,小明同学跳起来把一个排球打在离地 2 m远的地上,然后反弹碰到墙上,如果她跳起击球时的高度是 1.8 m,排球落地点离墙的距离是 6 m,假设球一直沿直线运动,球能碰到墙面离地多高的地方?
解:∵∠ABO=∠CDO=90°,∠AOB=∠COD,∴△AOB∽△COD.
解得 CD = 5.4m.
故球能碰到墙面离地 5.4m 高的地方.
例10 如图,△ABC 是一块锐角三角形材料,边 BC=120 mm,高 AD=80 mm,要把它加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别在 AB、AC 上,这个正方形零件的边长是多少?
解:设正方形 EFHG 为加工成的 正方形零件,边 GH 在 BC 上,顶点 E、F 分别在AB、 AC上,△ABC 的高 AD 与边 EF 相交于点 M,设正方形的 边长为 x mm.
∵ EF//BC,∴△AEF∽△ABC,
又∵ AM=AD-MD=80-x,
解得 x = 48.即这个正方形零件的边长是 48 mm.
初中人教版第二十七章 相似综合与测试复习课件ppt: 这是一份初中人教版第二十七章 相似综合与测试复习课件ppt,共22页。PPT课件主要包含了-12或,1-2等内容,欢迎下载使用。
初中数学人教版九年级下册第二十七章 相似综合与测试复习课件ppt: 这是一份初中数学人教版九年级下册第二十七章 相似综合与测试复习课件ppt,共31页。PPT课件主要包含了复习巩固,回顾一,相似多边形,定义性质,重点回顾,回顾二,相似三角形,回顾三,相似三角形的应用,回顾四等内容,欢迎下载使用。
初中数学人教版九年级下册第二十七章 相似综合与测试复习课件ppt: 这是一份初中数学人教版九年级下册第二十七章 相似综合与测试复习课件ppt,共18页。PPT课件主要包含了重热点二位似图形,评分说明,选择题,填空题,解答题等内容,欢迎下载使用。














