资料中包含下列文件,点击文件名可预览资料内容





还剩8页未读,
继续阅读
所属成套资源:湘教版数学初三下学期PPT课件(送教案)整套
成套系列资料,整套一键下载
- 2.3 垂径定理 课件+教案 课件 7 次下载
- 2.4 过不共线三点作圆 课件+教案 课件 6 次下载
- 2.5.1 直线与圆的位置关系 课件+教案 课件 6 次下载
- 2.5.2 圆的切线 第1课时 切线的判定 课件+教案 课件 5 次下载
- 2.5.2 圆的切线 第2课时 切线的性质 课件+教案 课件 5 次下载
- 2.5.3 切线长定理 课件+教案 课件 5 次下载
2.2.1 圆心角 课件+教案
展开
这是一份2.2.1 圆心角 课件+教案
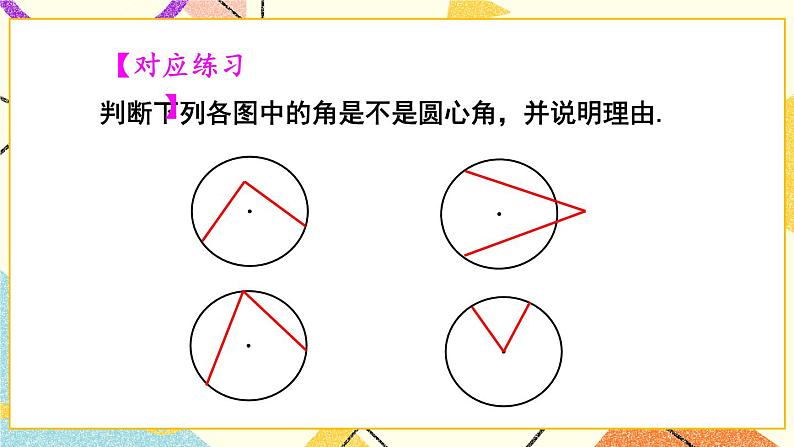
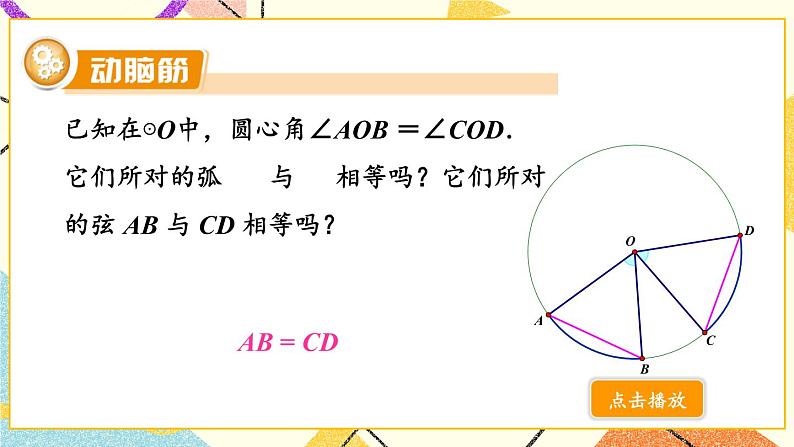
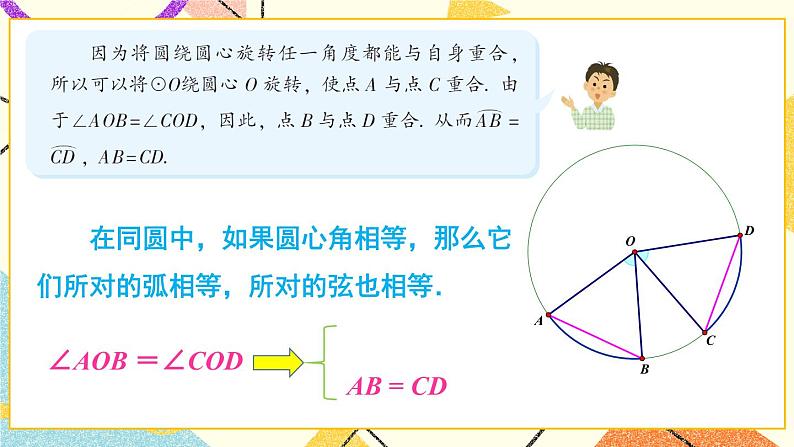
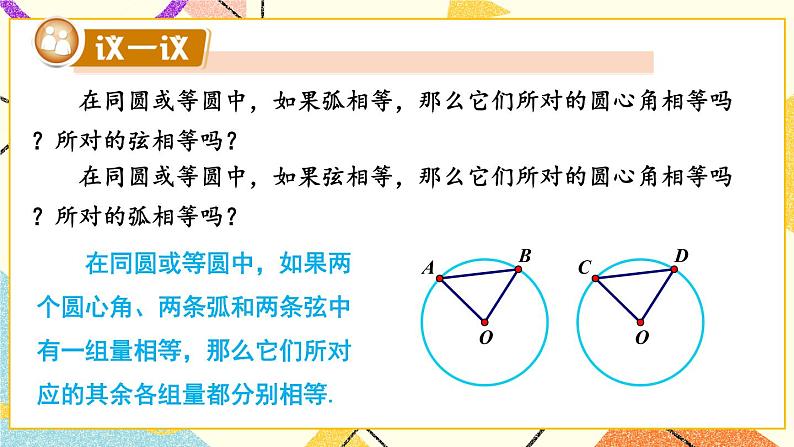
圆心角湘教·九年级下册探究新知观察图中的∠AOB, 可以发现它的顶点在圆心,角的两边与圆相交, 像这样的角叫作圆心角.我们把∠AOB 叫作 所对的圆心角, 叫作圆心角∠AOB 所对的弧. 在生活中,我们常遇到圆心角,如飞镖靶中有圆心角,还有手表的时针与分针所成的角等也是圆心角.判断下列各图中的角是不是圆心角,并说明理由.【对应练习】已知在⊙O中,圆心角∠AOB =∠COD.它们所对的弧 与 相等吗?它们所对的弦 AB 与 CD 相等吗?AB = CD 在同圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等.∠AOB =∠CODAB = CD 在同圆或等圆中,如果弧相等,那么它们所对的圆心角相等吗?所对的弦相等吗? 在同圆或等圆中,如果弦相等,那么它们所对的圆心角相等吗?所对的弧相等吗? 在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等. 如图,等边△ABC 的顶点 A,B,C 在⊙O 上,求圆心角 ∠AOB 的度数.解 ∵ △ABC 为等边三角形,∴ AB = BC = AC.∴ ∠AOB =∠BOC =∠COA .又∵ ∠AOB +∠BOC +∠COA = 360°,∴ ∠AOB = (∠AOB+∠BOC+∠COA) = × 360 ° = 120° .【教材P48页】1.在⊙O中,已知∠AOB = 40°, ,求∠COD的度数.练习解 ∵∴∠COD = ∠AOB = 40°【教材P48页】 2. 如图,在⊙O中,AB 是直径,∠AOE = 60°,点 C,D 是 的三等分点,求∠COE 的度数.解 ∵ ∠AOE = 60°, ∴∠BOE = 120°又∵点 C,D 是 的三等分点∴∠BOC = ∠COD = ∠DOE = 40°∴∠COE = 80°【教材P48页】随堂练习如图, 在☉O 中, ,∠A=30°,则∠B 的度数为( ) A. 150° B. 75° C. 60° D. 15°选自《创优作业》B2. 如图,在☉O 中,若 C 是 的中点, ∠OAB=50°, 则∠BOC 的度数为( ) A. 40° B. 45° C. 50° D. 60° 选自《创优作业》A3. 如图, AB 是 ☉O 的直径, BC , CD , DA 是☉O 的弦, 且 BC = CD = DA , 则∠BCD 的度数为( ) A. 100° B. 110° C. 120° D.135°选自《创优作业》C课堂小结 在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等.∠AOB =∠CODAB = CD 在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.∠AOB =∠CODAB = CD 课堂小结∠AOB =∠CODAB = CD AB = CD ∠AOB =∠COD
圆心角湘教·九年级下册探究新知观察图中的∠AOB, 可以发现它的顶点在圆心,角的两边与圆相交, 像这样的角叫作圆心角.我们把∠AOB 叫作 所对的圆心角, 叫作圆心角∠AOB 所对的弧. 在生活中,我们常遇到圆心角,如飞镖靶中有圆心角,还有手表的时针与分针所成的角等也是圆心角.判断下列各图中的角是不是圆心角,并说明理由.【对应练习】已知在⊙O中,圆心角∠AOB =∠COD.它们所对的弧 与 相等吗?它们所对的弦 AB 与 CD 相等吗?AB = CD 在同圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等.∠AOB =∠CODAB = CD 在同圆或等圆中,如果弧相等,那么它们所对的圆心角相等吗?所对的弦相等吗? 在同圆或等圆中,如果弦相等,那么它们所对的圆心角相等吗?所对的弧相等吗? 在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等. 如图,等边△ABC 的顶点 A,B,C 在⊙O 上,求圆心角 ∠AOB 的度数.解 ∵ △ABC 为等边三角形,∴ AB = BC = AC.∴ ∠AOB =∠BOC =∠COA .又∵ ∠AOB +∠BOC +∠COA = 360°,∴ ∠AOB = (∠AOB+∠BOC+∠COA) = × 360 ° = 120° .【教材P48页】1.在⊙O中,已知∠AOB = 40°, ,求∠COD的度数.练习解 ∵∴∠COD = ∠AOB = 40°【教材P48页】 2. 如图,在⊙O中,AB 是直径,∠AOE = 60°,点 C,D 是 的三等分点,求∠COE 的度数.解 ∵ ∠AOE = 60°, ∴∠BOE = 120°又∵点 C,D 是 的三等分点∴∠BOC = ∠COD = ∠DOE = 40°∴∠COE = 80°【教材P48页】随堂练习如图, 在☉O 中, ,∠A=30°,则∠B 的度数为( ) A. 150° B. 75° C. 60° D. 15°选自《创优作业》B2. 如图,在☉O 中,若 C 是 的中点, ∠OAB=50°, 则∠BOC 的度数为( ) A. 40° B. 45° C. 50° D. 60° 选自《创优作业》A3. 如图, AB 是 ☉O 的直径, BC , CD , DA 是☉O 的弦, 且 BC = CD = DA , 则∠BCD 的度数为( ) A. 100° B. 110° C. 120° D.135°选自《创优作业》C课堂小结 在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等.∠AOB =∠CODAB = CD 在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.∠AOB =∠CODAB = CD 课堂小结∠AOB =∠CODAB = CD AB = CD ∠AOB =∠COD
相关资料
更多









