





初中数学湘教版九年级下册第1章 二次函数综合与测试复习ppt课件
展开不共线三点确定二次函数的表达式
二次函数与一元二次方程的联系
知识点① 二次函数的概念及解析式
1.二次函数的概念:如果函数的表达式是自变量的二次多项式,那么,这样的函数称为二次函数。一般形式: y=ax²+bx+c (a,b,c是常数,a≠0)
1)三种解析式:①一般式:y=ax2+bx+c;②顶点式:y=a(x-h)2+k(a≠0),其中二次函数的顶点坐标是(h,k); ③交点式:y=a(x-x1)(x-x2),其中x1,x2为抛物线与x轴交点的横坐标.2)待定系数法:巧设二次函数的解析式;根据已知条件,得到关于待定系数的方程(组);解方程(组),求出待定系数的值,从而求出函数的解析式.
知识点② 二次函数的图象与性质
当x< 时, y随x的增大而减小;x> 时,y随x的增大而增大.
当x> 时,y随x的增大而减小; x< 时,y随x的增大而增大.
知识点③ 系数a、b、c符号确定
a决定抛物线的开口方向及开口大小
当a>0时,抛物线开口向上;当a<0时,抛物线开口向下.
决定抛物线与x轴的交点个数
决定抛物线与y轴的交点的位置
当c>0时,抛物线与y轴的交点在正半轴上;当c=0时,抛物线经过原点;当c<0时,抛物线与y轴的交点在负半轴上
b2-4ac>0时,抛物线与x轴有2个交点;b2-4ac=0时,抛物线与x轴有1个交点;b2-4ac<0时,抛物线与x轴没有交点
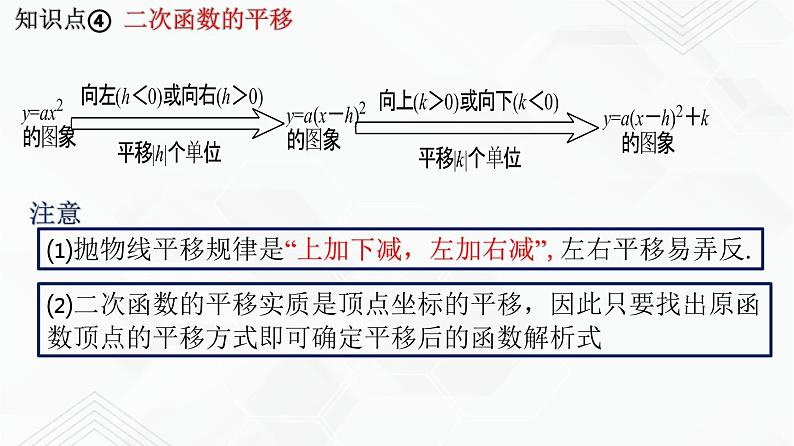
知识点④ 二次函数的平移
⑴抛物线平移规律是“上加下减,左加右减”,左右平移易弄反.
⑵二次函数的平移实质是顶点坐标的平移,因此只要找出原函数顶点的平移方式即可确定平移后的函数解析式
知识点⑤ 二次函数与一元二次方程
二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标 是一元二次方程ax2+bx+c=0的根. 当Δ=b2-4ac>0,两个不相等的实数根; 当Δ=b2-4ac=0,两个相等的实数根; 当Δ=b2-4ac<0,无实根
知识点⑥ 二次函数与不等式
抛物线y= ax2+bx+c=0 在x轴上方的部分点的纵坐标都为正,所对应的x的所有值就 是不等式ax2+bx+c>0的解集;在x轴下方的部分点的纵坐标均为负,所对应的x的值就是不等式ax2+bx+c<0的解集.
知识点⑦ 二次函数应用
据题意,①结合函数图象求出函数解析式;②确定自变量的取值范围;③根据图象,结合所求解析式解决问题.
若题目中未给出坐标系,则需要建立坐标系求解,建立的原则:①所建立的坐标系要使求出的二次函数表达式比较简单;②使已知点所在的位置适当(如在x轴,y轴、原点、抛物线上等),方便求二次函数丶表达式和之后的计算求解.
①分析问题中的数量关系,列出函数关系式;②研究自变量的取值范围;③确定所得的函数;④ 检验x的值是否在自变量的取值范围内,并求相关的值;⑤解决提出的实际问题..
解决最值应用题要注意两点:①设未知数,在“当某某为何值时,什么最大(最小)”的设问中,“某某”要设为自变量,“什么”要设为函数;②求解最值时,一定要考虑顶点(横、纵坐标)的取值是否在自变量的取值范围内.
①根据几何图形的性质,探求图形中的关系式;②根据几何图形的关系式确定二次函数解析式;③利用配方法等确定二次函数的最值,解决问题.
由于面积等于两条边的乘积,所以几何问题的面积的最值问题通常会通过二次函数来解决.同样需注意自变量的取值范围..
知识点❶二次函数的概念
例1、已知函数y=(m+3)xm2+4m-3+5是关于x的二次函数.(1)求m的值;
(2)当m为何值时,该函数图象的开口向上?
(3)当m为何值时,该函数有最大值?
解:∵函数图象的开口向上,∴m+3>0.∴m>-3.∴m=1.∴当m=1时,该函数图象的开口向上.
解:∵函数有最大值,∴m+3<0,∴m<-3.∴m=-5.∴当m=-5时,该函数有最大值.
2、抛物线 的开口向 ;对称轴为 ,顶点坐标为( ),当x 时,y随x的增大而增大。
3、已知抛物线 ,经过原点,则k= .
4、抛物线 的对称轴是直线 .
5、抛物线 开口 ,顶点坐标是 ,对称轴是 ,当x= 时,y有最 值为 .
7、如图所示为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0; ③a+b+c>0;④当-1<x<3时,y>0.其中正确的个数为( )A.1个 B.2个 C.3个 D.4个
7、如图所示为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc>0;②2a+b=0; ③a+c
8、把抛物线 向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
9、把抛物线 向右平移1个单位,然后向下平移3个单位后,其顶点在第四象限,则m取值范围是 。
∴ 顶点坐标为(m+1,m-2)
10、1)将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象,则y2= ;2)如图,P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x和抛物线y2交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t=( )
y2=2(x-2)2
解析:2)∵点A的坐标是(t,t), 点B的坐标是(t,2t2-8t+8), ∴AB=|t-(2t2-8t+8)|,
|t-(2t2-8t+8)|=|2-t|,解得t=1,3
(3)写出y随的x增大而减小的自变量的取值范围.(4)若方程 有两个不相等的实数根,求的取值范围.
12、已知关于x的一元二次方程mx2+(1-5m)x-5=0(m≠0).
(1)求证:无论m为任何非零实数,此方程总有两个实数根;
(2)若抛物线y=mx2+(1-5m)x-5与x轴交于A(x1,0)、B(x2,0)两点,且|x1-x2|=6,求m的值;
(3)若m>0,点P(a,b)与Q(a+n,b)在(2)中的抛物线上(点P、Q不重合),求代数式4a2-n2+8n的值.
(1)证明:∵Δ=(1-5m)2-4m×(-5)=1+25m2-10m+20m=25m2+10m+1=(5m+1)2≥0,∴无论m为任何非零实数,此方程总有两个实数根;
13.如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.(1)求抛物线的解析式和顶点坐标;(2)当0<x<3时,求y的取值范围;(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.
解:(1)把A(﹣1,0)、B(3,0)分别代入y=x2+bx+c中,得:
∴抛物线的解析式为y=x2﹣2x﹣3.∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴顶点坐标为(1,﹣4).(2)由图可得当0<x<3时,﹣4≤y<0.(3)∵A(﹣1,0)、B(3,0), ∴AB=4.设P(x,y),则S△PAB= AB•|y|=2|y|=10,
∴|y|=5,∴y=±5.①当y=5时,x2﹣2x﹣3=5,解得:x1=﹣2,x2=4,此时P点坐标为(﹣2,5)或(4,5);②当y=﹣5时,x2﹣2x﹣3=﹣5,方程无解;综上所述,P点坐标为(﹣2,5)或(4,5).
知识点⑥二次函数综合应用
14.如图,抛物线y=x2+bx+c与x轴交于点A和点B(3,0), 与y轴交于点C(0,3).(1)求抛物线的解析式;(2)若点M是抛物线在x轴下方上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值;(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
解:(1)将点B(3,0)、C(0,3)代入抛物线y=x2+bx+c中,得:
(2)∵直线BC:y=kx+b过(3,0)和(0,3)
∴抛物线的解析式为y=x2﹣4x+3
∴直线BC的解析式为y=﹣x+3.
∴点N的坐标为(m,﹣m+3).
由点M在抛物线y=x2﹣4x+3上
∴点M的坐标为(m,m2﹣4m+3),
由x2﹣4x+3=0得
∵点M是抛物线在x轴下方上的动点
14.如图,抛物线y=x2+bx+c与x轴交于点A和点B(3,0), 与y轴交于点C(0,3)(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
设对称轴l上存在点P,则P(2,n)
△PBN为等腰三角形分三种情况:
(1)求出w与x的函数关系式;(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?
19.九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
解:(1)当1≤x≤50时,设售价y与时间x的关系式为y=kx+b(k≠0)∵y=kx+b经过点(0,40)、(50,90)
∴售价y与时间x的函数关系式为y=x+40;
当50<x≤90时,y=90.
当1≤x≤50时,w=(y﹣30)•p =(x+40﹣30)(﹣2x+200) =﹣2x2+180x+2000;当50<x≤90时,w=(90﹣30)(﹣2x+200) =﹣120x+12000.
由数据销售量p与时间x成一次函数关系,p=mx+n∵p=mx+n过点(60,80)、(30,140)
∴p=﹣2x+200(0≤x≤90,且x为整数),
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?
2)当1≤x≤50时,w=﹣2x2+180x+2000=﹣2(x﹣45)2+6050,∵a=﹣2<0且1≤x≤50,∴当x=45时,w取最大值,最大值为6050元.当50<x≤90时,w=﹣120x+12000,∵k=﹣120<0,w随x增大而减小,∴当x=50时,w取最大值,最大值为6000元.∵6050>6000,∴当x=45时,w最大,最大值为6050元.即销售第45天时,当天获得的销售利润最大,最大利润是6050元.
初中数学湘教版九年级下册3.1 投影备课课件ppt: 这是一份初中数学湘教版九年级下册3.1 投影备课课件ppt,共20页。PPT课件主要包含了知识点❶投影的概念,照射光线叫做投影线,投影线,投影面,练一练,平行投影,中心投影,平行投影和中心投影,A3B3,点A3B3等内容,欢迎下载使用。
初中湘教版第2章 圆综合与测试复习课件ppt: 这是一份初中湘教版第2章 圆综合与测试复习课件ppt,共20页。PPT课件主要包含了知识网络,圆的定义及其相关概念,圆的有关性质,圆的对称性,轴对称性,垂径定理,中心对称性,圆周角,圆周角定理及其推论,与圆有关的位置关系等内容,欢迎下载使用。
数学湘教版2.3 垂径定理背景图课件ppt: 这是一份数学湘教版2.3 垂径定理背景图课件ppt,共19页。PPT课件主要包含了思考与探究,①圆是轴对称图形吗,②它的对称轴是什么,圆是轴对称图形,无数条,线段APBP,证一证,ADBD,ACBC,∴APBP等内容,欢迎下载使用。












