湘教版数学九年级下册 2.2.2圆周角（2）》课件+教案

这是一份湘教版数学九年级下册 2.2.2圆周角（2）》课件+教案，文件包含湘教版数学九年级下册222圆周角2》课件pptx、湘教版数学九年级下册222圆周角2》教案doc等2份课件配套教学资源，其中PPT共23页， 欢迎下载使用。

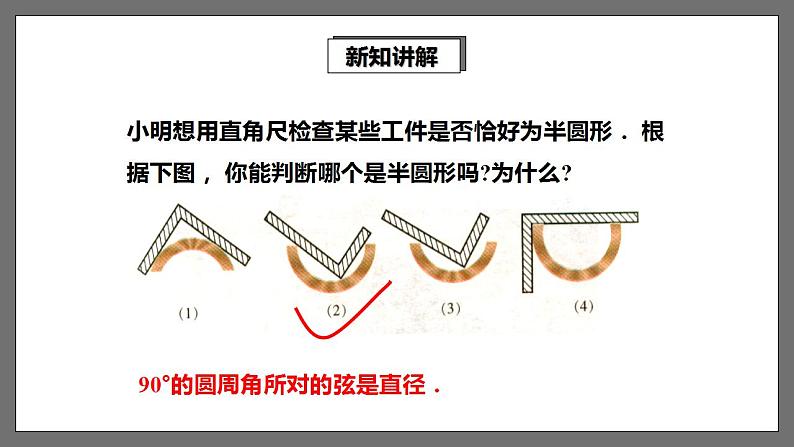
2.2.2圆周角（2）① 角的顶点在圆上．② 角的两边都与圆相交．顶点在圆上，并且两边都和圆相交的角叫圆周角．1、什么是圆周角？圆周角有何特征？导入新知2、圆周角定理圆周角的度数等于它所对弧上的圆心角度数的一半．3、圆周角定理的推论在同圆（或等圆）中，同弧或等弧所对的圆周角相等；相等的圆周角所对的弧也相等．导入新知探究点一 直径所对的圆周角的性质．1、半圆或直径所对的圆周角等于多少度？2、90°的圆周角所对的弦是否是直径？新知讲解探究活动一如图，AB是⊙O的直径，那么∠C1，∠C2，∠C3的度数分别是多少呢？直径所对的圆周角是直角．新知讲解探究活动二如图，A，B，C为圆周上三点，若已知∠C=90°，它所对的弦AB是不是直径？要求：1、先猜想，再证明； 2、同桌之间合作探究； 3、总结做题的方法规律．新知讲解90°的圆周角所对的弦是直径．新知讲解小明想用直角尺检查某些工件是否恰好为半圆形． 根据下图， 你能判断哪个是半圆形吗?为什么?90°的圆周角所对的弦是直径．新知讲解例3　如图，BC是⊙O的直径，∠ABC=60°，点D在⊙ O上，求∠ADB的度数．解：∵BC是⊙O的直径，∴∠BAC=90°．又 ∠ABC=60°，∴∠C=30°．∴∠ADB=∠C=30°．新知讲解如图，A，B，C，D是⊙O上的四点，顺次连接A，B，C，D四点，得到四边形ABCD．若一个四边形各顶点都在同一个圆上，那么，这个四边形叫做圆内接四边形．这个圆叫做这个四边形的外接圆．新知讲解四边形ABCD中两组对角∠A与∠C，∠B与∠D有什么关系？连接OB，OD．新知讲解由四边形内角和定理可知，∠ABC+ ∠ ADC=180°．由此可得到以下结论：圆内接四边形的对角互补．几何语言：∵四边形ABCD内接于⊙O，∴∠A+ ∠ C=180°，∠B+ ∠ D=180°．新知讲解如果延长BC到E，那么∠A与∠DCE会有怎样的关系呢？证明猜想：∵∠DCE+∠BDC=180°，又∠A+∠BCD=180°，∴∠A=∠DCE．我们把∠A叫做∠DCE的内对角．因为∠A是与∠DCE相邻的内角∠DCB的对角．圆内接四边形的任意一个外角等于它的内对角．新知讲解圆内接四边形定理：圆的内接四边形的对角互补，并且任意一个外角等于它的内对角．几何语言：∵四边形ABCD内接于⊙O，∴∠A+∠C=180°，∠B+∠ADC=180°，∴∠B=∠CDE．新知讲解例4 如图，四边形ABCD为⊙O圆的内接四边形，已知∠BOD=100°．求∠BAD及∠BCD的度数．新知讲解∵∠BCD+∠BAD=180°，∴∠BCD=180°-∠BAD= 130° ．新知讲解1、四边形ABCD内接于⊙O，则∠A+∠C=______，∠B+∠ADC= ______；若∠B=800， 则∠ADC=______ ∠CDE=______．180° 180° 100° 80° 巩固提升2、四边形ABCD内接于⊙O，∠AOC=1000．则∠B=______，∠D= ______ ；若∠A:∠C=1:3，则∠A= ______．50° 130° 45° 巩固提升4、如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD的度数是____．32°3、如图所示，已知AB是半圆O的直径，∠BAC=22°，则∠B=________度．68巩固提升5、如图所示，四边形ABCD为⊙O的内接四边形，∠BOD=98°，求∠A和∠C的度数．∵四边形ABCD是圆内接四边形，∴∠C=180°-∠A=131°．巩固提升6、如图，⊙O的直径AB=10 cm，C是⊙O上的一点，∠ABC =30°．求AC的长．解：∵ AB是⊙O的直径，∴ ∠ACB= 90º．∵ ∠ABC =30°，巩固提升1、直径（或半圆）所对的圆周角是直角；2、90°的圆周角所对的弦是直径；3、圆内接四边形和四边形的外接圆；4、圆的内接四边形的对角互补．课堂小结