
- 矩形的性质 课件 课件 7 次下载
- 菱形的性质 课件 课件 3 次下载
- 第十五章 四边形 复习课件 课件 2 次下载
- 15.3平行四边形的性质与判定_课件1 课件 4 次下载
- 15.6中心对称图形_课件1 课件 4 次下载
北京课改版八年级下册15.5 三角形中位线定理教学演示ppt课件
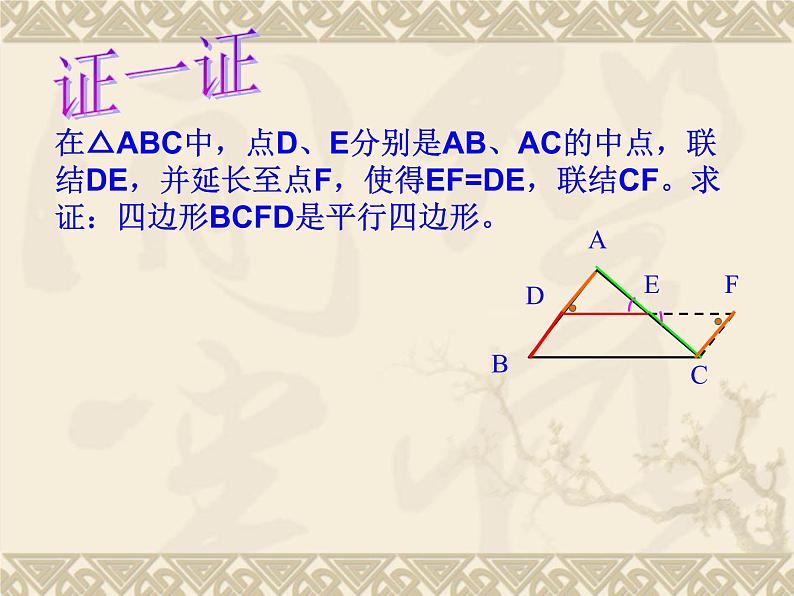
展开在△ABC中,点D、E分别是AB、AC的中点,联结DE,并延长至点F,使得EF=DE,联结CF。求证:四边形BCFD是平行四边形。
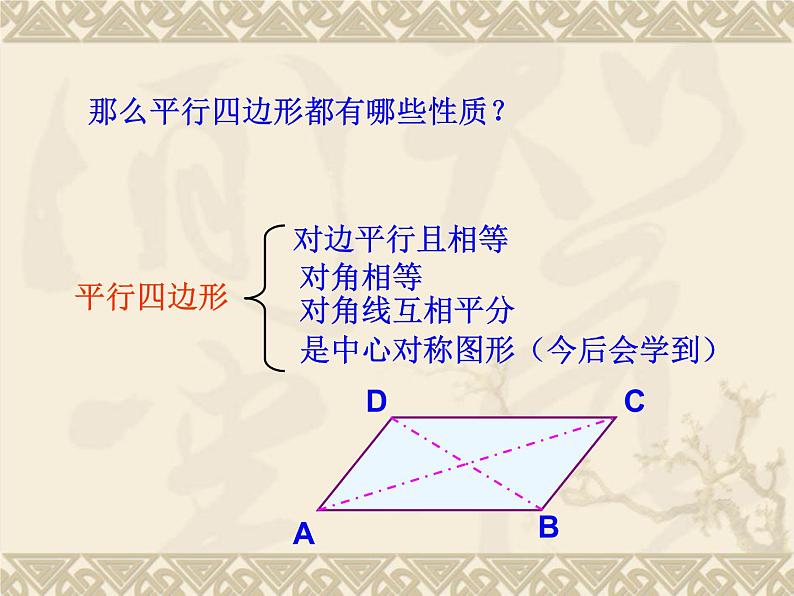
那么平行四边形都有哪些性质?
是中心对称图形(今后会学到)
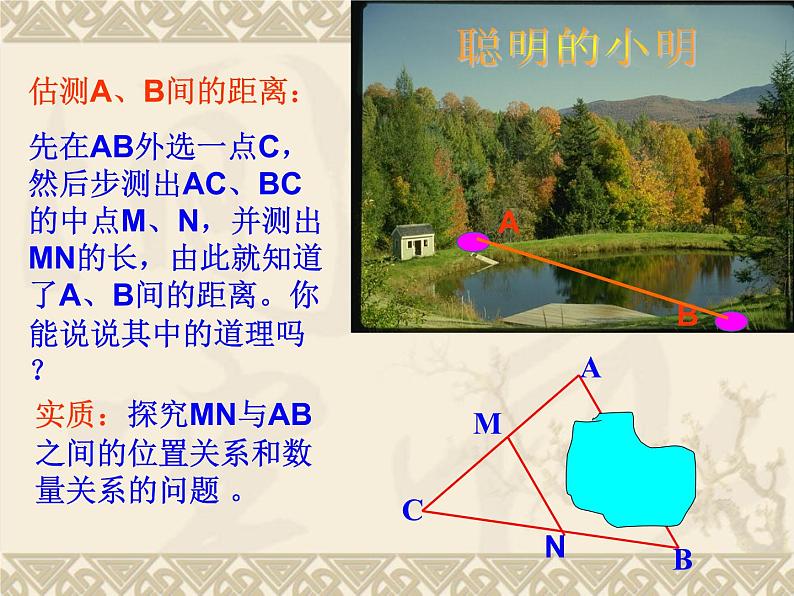
先在AB外选一点C,然后步测出AC、BC的中点M、N,并测出MN的长,由此就知道了A、B间的距离。你能说说其中的道理吗?
实质:探究MN与AB之间的位置关系和数量关系的问题 。
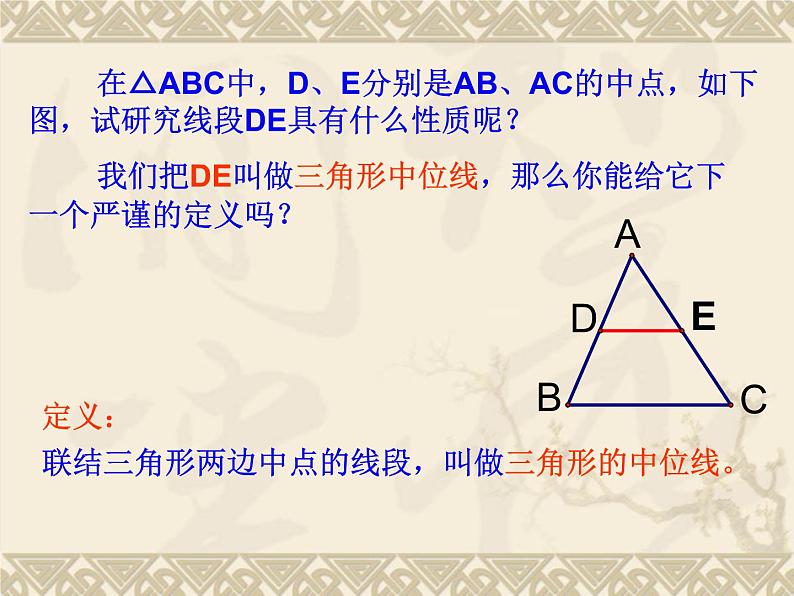
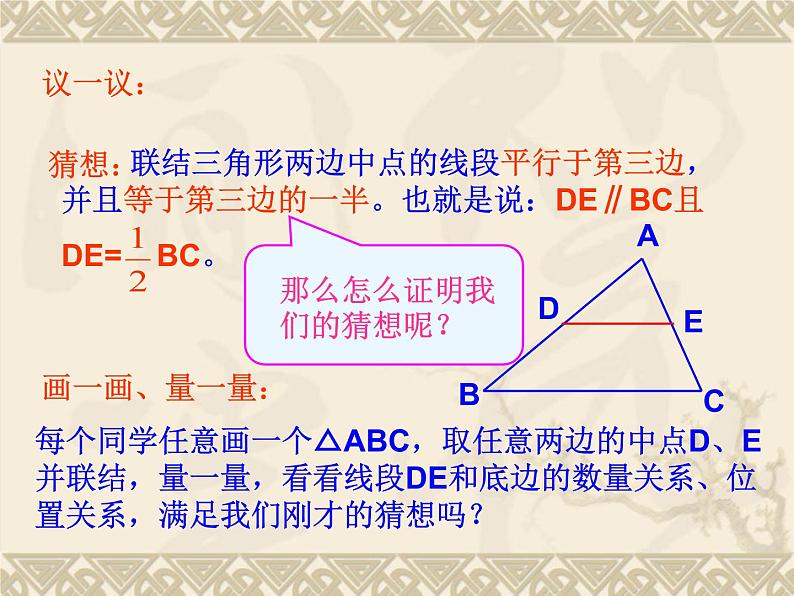
在△ABC中,D、E分别是AB、AC的中点,如下图,试研究线段DE具有什么性质呢?
联结三角形两边中点的线段,叫做三角形的中位线。
我们把DE叫做三角形中位线,那么你能给它下一个严谨的定义吗?
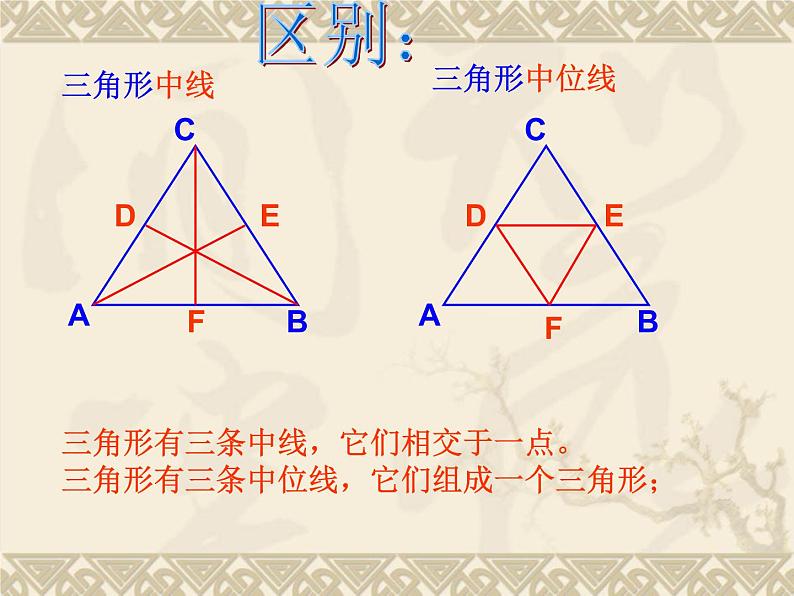
三角形有三条中线,它们相交于一点。三角形有三条中位线,它们组成一个三角形;
每个同学任意画一个△ABC,取任意两边的中点D、E并联结,量一量,看看线段DE和底边的数量关系、位置关系,满足我们刚才的猜想吗?
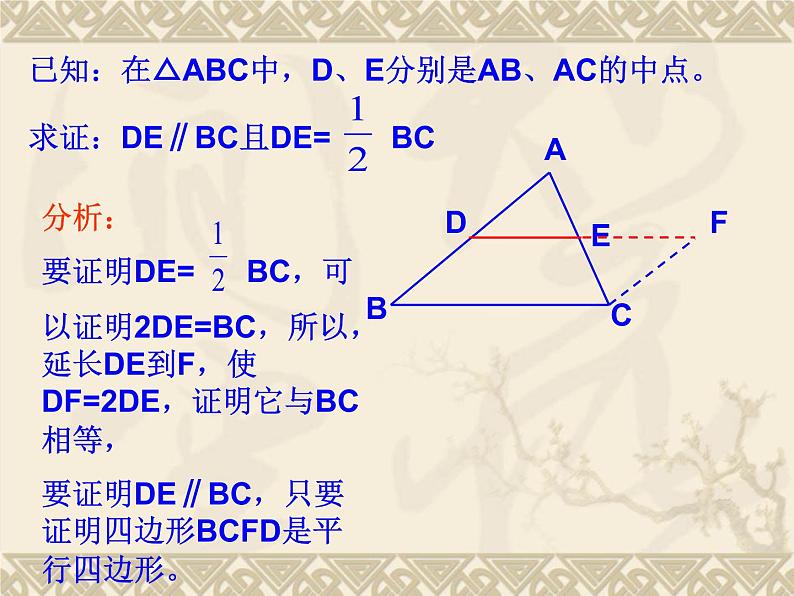
已知:在△ABC中,D、E分别是AB、AC的中点。
联结三角形两边中点的线段平行于第三边,并且等于第三边的一半。
在△ABC中,∵AD=DB,AE=EC
强调:中位线定理在同一条件下有两个结论,一是表明位置关系,一是表明数量关系,应用时要根据需要而选择。
作CF∥AB,与DE的延长线交于点F
四边形BCFD是平行四边形
延长中位线到点F,使得EF=DE,联结DC、AF、CF根据对角线互相平分
∴四边形ADCF是平行四边形
当一个命题有几种证法时,选取较简捷的方法。
估测A、B间的距离:先在AB外选一点C,然后步测出AC、BC的中点M、N,并测出MN的长,由此就知道了A、B间的距离。你能说说其中的道理吗?
已知,如图,在△ABC中,AD=DB,BF =FC,AE=EC求证:AF、DE互相平分。
证明:联结DF、EF
∵AD=DB,BF=FC
∴DF∥AC,同理FE∥AB
∴四边形ADFE是平行四边形
∴AF、DE互相平分
你还有其他的证明方法吗?
如左下图,△ABC中,D、E、F 分别为AB、BC、CA的中点,∠DEF = ∠BAC 吗?
如右下图,△ABC中,AG 是 BC边的高,D、F是AB、AC的中点,∠DGF = BAC 吗?
把上面两个图形合并在一起,如下图,根据合并后的图形编一道题,并证明你的结论。
1,本节课你通过怎样的学习收获到了什么?
2,证明三角形中位线定理的关键在于什么?
3,定理有几个结论,如何应用?
两个结论,一是表明位置关系,一是表明数量关系,应用时要根据需要而选择。
1、分类讨论:顺次联结什么样的四边形各边中点的线段所围城的四边形是平行四边形、矩形、菱形、正方形?
北京课改版八年级下册15.5 三角形中位线定理课堂教学ppt课件: 这是一份北京课改版八年级下册15.5 三角形中位线定理课堂教学ppt课件,共12页。PPT课件主要包含了概念形成等内容,欢迎下载使用。
三角形中位线定理PPT课件免费下载: 北京课改版初中数学八年级下册课文《三角形中位线定理》,完整版PPT课件免费下载,优秀PPT背景图搭配,精美的免费ppt模板。轻松备课,欢迎免费下载使用。
初中数学北京课改版八年级下册15.5 三角形中位线定理课前预习ppt课件: 这是一份初中数学北京课改版八年级下册15.5 三角形中位线定理课前预习ppt课件,













