北京课改版八年级下册15.6 中心对称图形课文内容ppt课件

这是一份北京课改版八年级下册15.6 中心对称图形课文内容ppt课件，共28页。PPT课件主要包含了太极图，飞机的螺旋桨，做一做，中心对称图形，想一想，圆心是它的对称中心，中心对称图形的性质，练习３，练习４，练习５等内容，欢迎下载使用。

图中的图形有怎样的特点呢？
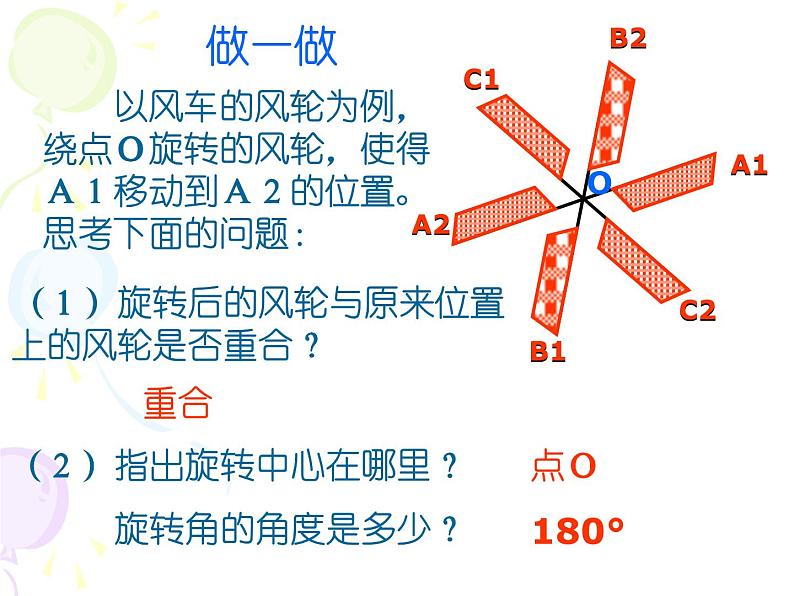
　　以风车的风轮为例，绕点Ｏ旋转的风轮，使得Ａ１移动到Ａ２的位置。思考下面的问题：
（１）旋转后的风轮与原来位置上的风轮是否重合？
（２）指出旋转中心在哪里？　　　旋转角的角度是多少？
（１）旋转后的图形与原来位置上的图形是否重合？
3）对于其他四个图形，请你也像上面一样 进行研究，回答同样的问题。
　　一般地，在同一平面内，一个图形绕某一个点旋转180°，如果旋转前、后的图形相互重合，那么这个图形叫做中心对称图形（pint symmetry figure），这个点叫做它的对称中心（center f symmetry）。
你在什么地方见到过中心对称图形？
　　在我们学习过的图形中，如线段、圆、等边三角形、平行四边形等，哪些是中心对称图形？哪些不是？
　　线段ＡＢ绕它的中点旋转180°后，它的两个端点互换了位置，旋转后的线段和原线段重合。
线段的中点是它的对称中心。
因此，线段是中心对称图形，
　　圆Ｏ绕它的圆心旋转180°后，它的每一条直径的两个端点互换了位置，旋转后的圆和原来的圆重合。
因此，圆是中心对称图形，
　　正三角形ABC绕它的外心（三条中垂线的交点）旋转180°后，它的每一条边的两个端点没有互换了位置，旋转后的正三角形不和原正三角形重合。
正三角形没有对称中心。
因此，正三角形不是中心对称图形，
　　平行四边形ABCD绕它对角线的交点O旋转180°后，它的每一条对角线的两个端点互换了位置，旋转后的平行四边形和原平行四边形重合。
对角线的交点是对称中心。
因此，平行四边形是中心对称图形，
中心对称图形的判断方法和步骤：
　　１．图形绕它一点旋转180°后，它的点互换了位置，说明旋转后的图形和原图形重合。
３．指明该图形的对称中心。
２．判断该图形是中心对称图形，
　　中心对称图形上的每一对对应点所连成的线段都被对称中心平分。
　　　　　练　习１　　所学的其它几何图形是不是中心对称图形？为什么？
　　线段、角、三角形、等腰三角形、等边三角形、直角三角形、四边形、平行四边形、矩形、菱形、正方形、梯形、等腰梯形、直角梯形、圆
练习２　判断是否为中心对称图形，并指明对称中心。
在平面上一个菱形绕它的中心旋转，使它与原来的菱形重合，那么旋转角度至少是（ 　 ）　　 A．180°        B． 90°       C． 270°    D． 360°   
下列说法中正确的是（　　）．A．矩形的每一条对角线都是矩形的对称轴B．平行四边形对角线的交点是平行四边形的对称中心C．菱形是轴对称图形，但不是中心对称图形D．中心对称图形就是中心对称
　　类比轴对称图形与轴对称的关系区分中心对称图形和中心对称
　　五角星是不是中心对称图形？为什么？
点Ｏ是正六边形ABCDEF的中心。
（１）指出这个轴对称图形的全部对称轴。
（２）这个正六边形绕点Ｏ旋转多少度后能和原来的图形重合？对于其他的正多边形能得到什么类似的结论？
旋转360°/n或其整数倍；
边数为偶数的正多边形都是中心对称图形。