
初中第十三章 轴对称综合与测试单元测试课堂检测
展开一.选择题
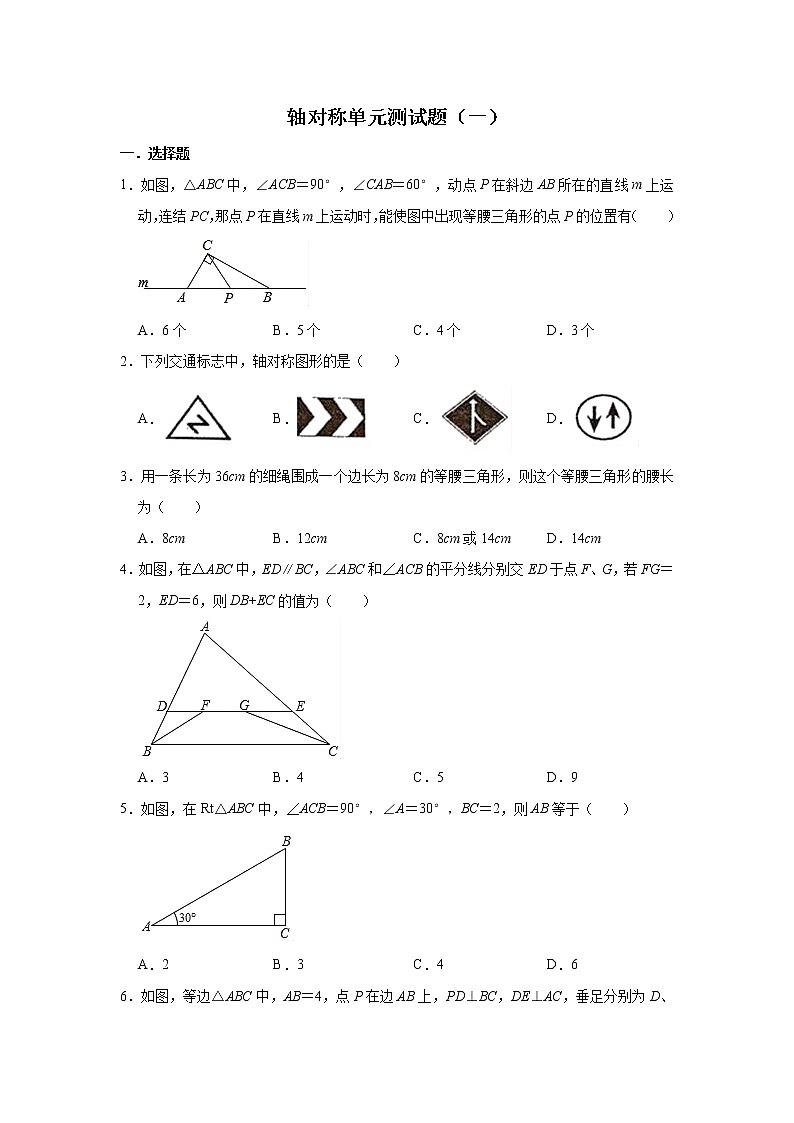
1.如图,△ABC中,∠ACB=90°,∠CAB=60°,动点P在斜边AB所在的直线m上运动,连结PC,那点P在直线m上运动时,能使图中出现等腰三角形的点P的位置有( )
A.6个B.5个C.4个D.3个
2.下列交通标志中,轴对称图形的是( )
A.B.C.D.
3.用一条长为36cm的细绳围成一个边长为8cm的等腰三角形,则这个等腰三角形的腰长为( )
A.8cmB.12cmC.8cm或14cmD.14cm
4.如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点F、G,若FG=2,ED=6,则DB+EC的值为( )
A.3B.4C.5D.9
5.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,则AB等于( )
A.2B.3C.4D.6
6.如图,等边△ABC中,AB=4,点P在边AB上,PD⊥BC,DE⊥AC,垂足分别为D、E,设PA=x,若用含x的式子表示AE的长,正确的是( )
A.2﹣xB.3﹣xC.1D.2+x
7.两个等腰三角形的顶角相等,其中一个三角形的两边分别为2,4,另一个三角形底边为12,则腰长为( )
A.6B.12C.6或24D.24
8.等腰三角形一腰上的高与另一腰的夹角为25°,则其底角为( )
A.65°B.32.5°
C.32.5°或57.5°D.32.5°或65°
9.已知坐标系中点P(2﹣n,1﹣m)与点Q关于x轴对称,若m>1,n<2,则点Q在( )
A.第一象限B.第二象限C.第三象限D.第四象限
10.如图,D为△ABC边上一点,连接CD,则下列推理过程中,因果关系与所填依据不符的是( )
A.∵AD=BD,∠ACD=∠BCD(已知)∴AC=BC(等腰三角形三线合一)
B.∵AC=BC,AD=BD(已知)∴∠ACD=∠BCD(等腰三角形三线合一)
C.∵AC=BC,∠ACD=∠BCD(已知)∴AD=BD(等腰三角形三线合一)
D.∵AC=BC,AD=BD(已知)∴CD⊥AB(等腰三角形三线合一)
二.填空题
11.若一条长为24cm的细线能围成一边长等于6cm的等腰三角形,则该等腰三角形的腰长为 cm.
12.如果等腰△ABC的两边分别长为4和9,则其周长为 .
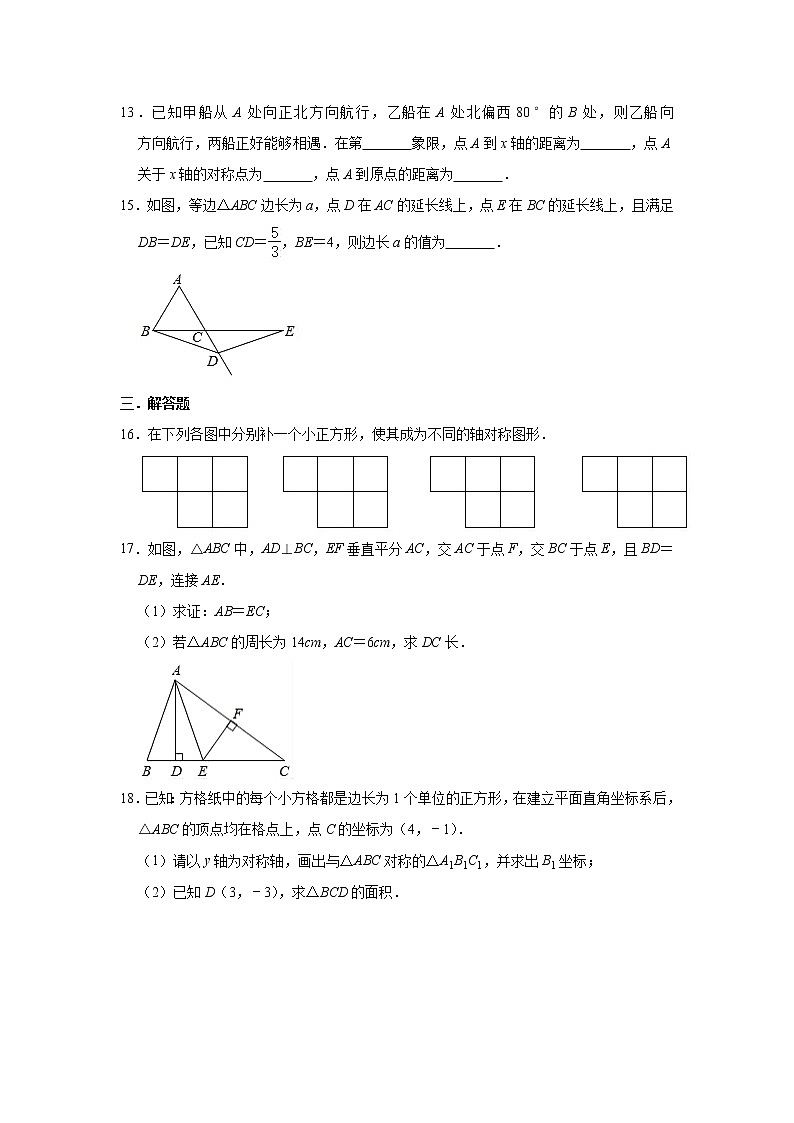
13.已知甲船从A处向正北方向航行,乙船在A处北偏西80°的B处,则乙船向 方向航行,两船正好能够相遇.在第 象限,点A到x轴的距离为 ,点A关于x轴的对称点为 ,点A到原点的距离为 .
15.如图,等边△ABC边长为a,点D在AC的延长线上,点E在BC的延长线上,且满足DB=DE,已知CD=,BE=4,则边长a的值为 .
三.解答题
16.在下列各图中分别补一个小正方形,使其成为不同的轴对称图形.
17.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.
(1)求证:AB=EC;
(2)若△ABC的周长为14cm,AC=6cm,求DC长.
18.已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并求出B1坐标;
(2)已知D(3,﹣3),求△BCD的面积.
19.如图,在平面直角坐标系xOy中,△ABC与△A1B1C1的顶点都在格点上,现将△ABC作以下两次全等变换:
①将△ABC作关于直线l的轴对称变换,得到△A1B1C1;
②再将△A1B1C1作关于x轴的轴对称变换,得到△A2B2C2,其中点A,A1,A2为对应点,B,B1,B2为对应点.
(1)画出直线l与△A2B2C2;
(2)观察两次变换后点坐标的变化规律,若△ABC的边上有一点P(a,b),则点P在△A2B2C2中的对应点P2的坐标应为 .
参考答案与试题解析
一.选择题
1.【解答】解:如图所示:以B为圆心,BC长为半径画弧,交直线m于点P4,P2,
以A为圆心,AC长为半径画弧,交直线m于点P1,P3,
边AC和BC的垂直平分线都交于点P3位置,
因此出现等腰三角形的点P的位置有4个,
故选:C.
2.【解答】解:A、不是轴对称图形,不合题意;
B、是轴对称图形,符合题意.
C、不是轴对称图形,不合题意;
D、不是轴对称图形,不合题意;
故选:B.
3.【解答】解:分两种情况讨论:
(1)如果8cm长的边为底边,设腰长为xcm,则有x+x+8=36cm,
解得x=14,
(2)如果8cm长的边为腰,设底边为xcm,则有8+8+x=36cm,
解得x=20.
因为8+8<20,出现两边的和小于第三边的情况,
所以不能围成腰长是8cm的等腰三角形,
由以上讨论可知,这个等腰三角形的腰长为14cm,
故选:D.
4.【解答】解:∵ED∥BC,
∴∠DFB=∠FBC,∠EGC=∠GCB,
∵∠DBF=∠FBC,∠ECG=∠GCB,
∴∠DFB=∠DBF,∠ECG=∠EGC,
∴BD=DF,CE=GE,
∵FG=2,ED=6,
∴DB+EC=DF+GE=ED﹣FG=6﹣2=4,
故选:B.
5.【解答】解:∵在Rt△ABC中,∠A=30°,BC=2,
∴AB=2CB=4,
故选:C.
6.【解答】解:∵△ABC是等边三角形,
∴AB=BC=AC=4,∠B=∠C=60°,
∵PD⊥BC,DE⊥AC,
∴BD=PB,CE=CD,
∵PA=x,
∴BP=4﹣x,
∴BD=PB=2﹣x,
∴CD=4﹣(2﹣x)=2+x,
∴CE=1+x,
∴AE=4﹣(1+x)=3﹣x,
故选:B.
7.【解答】解:依题意得:三角形的底边长为2,腰长为4,
根据两三角形相似可知另一个三角形的腰长=4×=24.
故选:D.
8.【解答】解:①如图1,当等腰三角形的顶角是钝角时,腰上的高在外部,
根据三角形的一个外角等于与它不相邻的两个内角的和,可得顶角是90°+25°=115°,
则其底角为(180°﹣115°)÷2=32.5°;
②如图2,当等腰三角形的顶角是锐角时,腰上的高在其内部,
故顶角是90°﹣25°=65°,
则其底角为(180°﹣65°)÷2=57.5°.
故选:C.
9.【解答】解:∵点P(2﹣n,1﹣m)与点Q关于x轴对称,
∴点Q的坐标为(2﹣n,m﹣1),
又∵m>1,n<2,
∴2﹣n>0,m﹣1>0,
∴点Q在第一象限.
故选:A.
10.【解答】解:A.∵AD=BD,∠ACD=∠BCD(已知),
∴AC=BC(等腰三角形三线合一),
条件没有等腰三角形,
故因果关系与所填依据不符;
B.∵AC=BC,AD=BD(已知),
∴∠ACD=∠BCD(等腰三角形三线合一),
因果关系与所填依据相符;
C.∵AC=BC,∠ACD=∠BCD(已知),
∴AD=BD(等腰三角形三线合一),
因果关系与所填依据相符;
D.∵AC=BC,AD=BD(已知),
∴CD⊥AB(等腰三角形三线合一),
因果关系与所填依据相符;
故选:A.
二.填空题(共5小题)
11.【解答】解:若6cm为底时,腰长应该是(24﹣6)=9cm,
故三角形的三边分别为6cm、9cm、9cm,
∵6+9=15>9,
故能围成等腰三角形,
若6cm为腰时,底边长应该是24﹣6×2=12,
故三角形的三边为6cm、6cm、12cm,
∵6+6=12,
∴以6cm、6cm、12cm为三边不能围成三角形,
综上所述,腰长是9cm,
故答案为:9.
12.【解答】解:当4为底时,其它两边都为9,4、9、9可以构成三角形,周长为22,
当4为腰时,其它两边为4和9,4、4、9不可以构成三角形.
故答案为:22.
13.【解答】解:如图所示,甲船沿AD方向航行,
∵两船的速度相同,起始时间相同,两船正好能够相遇,
∴两船航行的路径就是等腰三角形的腰长,
∴∠DAB=∠ABC=80°,
又∵∠ABG=∠BAD=80°,
∴∠CBF=180°﹣∠ABC﹣∠ABG=180°﹣80°﹣80°=20°,
即乙船向北偏东20°方向航行,
故答案为:北偏东20°.
14.【解答】解:点A(6,﹣8)在第四象限,点A到x轴的距离为8,点A关于x轴的对称点为(6,8),点A到原点的距离为=10.
故答案为:四,8,(6,8),10.
15.【解答】解:过D作DF⊥BE于F,
∵DB=DE,
∴△DBE是等腰三角形,
∵BE=4,
∴BF=EF=2,
∵△ABC是等边三角形,
∴∠ACB=60°,
∴∠DCF=60°,
∴∠CDF=30°,
∴CF=CD=×=,
∴BC=2﹣=,
∴a=,
故答案为:.
三.解答题(共4小题)
16.【解答】解:如图所示:
17.【解答】(1)证明:∵EF垂直平分AC,
∴AE=EC,
∵AD⊥BC,BD=DE,
∴AB=AE,
∴AB=EC;
(2)解:∵△ABC的周长为14cm,
∴AB+BC+AC=14(cm),
∵AC=6cm,
∴AB+BC=8(cm),
∵AB=EC,BD=DE,
∴DC=DE+EC=(AB+BC)=4(cm).
18.【解答】解:(1)如图所示:△A1B1C1即为所求,
B1坐标(﹣1,﹣4);
(2)△BCD的面积:2×3﹣×2×1﹣×2×1﹣1×3=.
19.【解答】解:(1)如图,直线l与△A2B2C2即为所求;
(2)点P2的坐标为(﹣b,a).
故答案为:(﹣b,a).
初中数学人教版八年级上册第十三章 轴对称综合与测试单元测试练习: 这是一份初中数学人教版八年级上册第十三章 轴对称综合与测试单元测试练习,共9页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学人教版八年级上册第十三章 轴对称综合与测试单元测试精练: 这是一份初中数学人教版八年级上册第十三章 轴对称综合与测试单元测试精练,共10页。试卷主要包含了点M,下列图形中对称轴最多的是,下列说法正确的是,如图等内容,欢迎下载使用。
人教版八年级上册13.1 轴对称综合与测试课时作业: 这是一份人教版八年级上册13.1 轴对称综合与测试课时作业,共12页。试卷主要包含了下列图片中,是轴对称图形的是,下列图形对称轴最多的是,第七届世界军人运动会在武汉,有下列说法等内容,欢迎下载使用。













