【全套精品专题】通用版八年级上数学学案 第一讲 轴对称与轴对称图形（知识梳理+同步练习无答案）

轴对称图像常考图像的判断，一般较简单；轴对称的性质主要是考查对称性；线段垂直平分线的定义及其性质是本讲的重点和难点内容，需重点掌握。

1.把一个图形沿着某一条直线翻折，如果直线两旁的部分能够互相重合，那么称这个图形是轴对称图形.

2.把一个图形沿着某一条直线翻折，如果它能够与另一个图形重合，那么称这两个图形关于这条直线对称，也称这两个图形成轴对称，这条直线叫做对称轴.

3.轴对称图形和两个图形成轴对称的区别和联系：

例1、下列图形中，是轴对称图形的是____________，其中只有1条对称轴的是________，有3条对称轴的是________，有2条对称轴的是________．（只要求写图形序号）

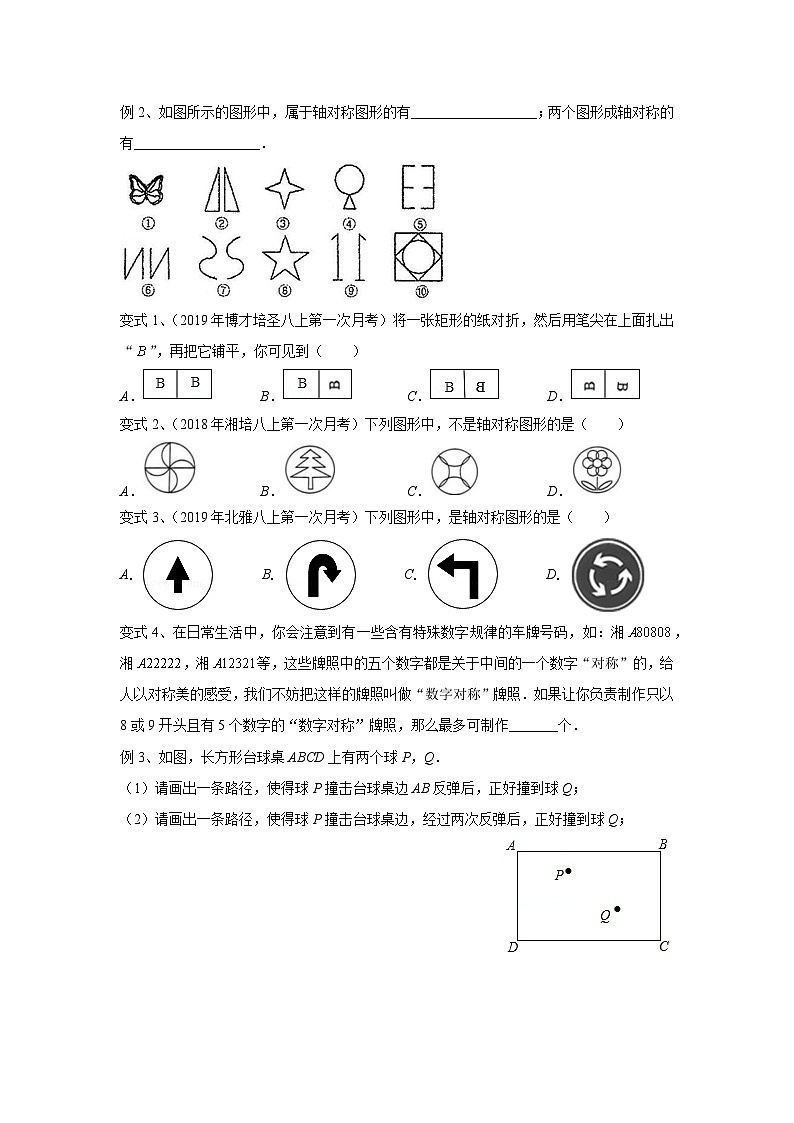
例2、如图所示的图形中，属于轴对称图形的有__________________；两个图形成轴对称的有__________________．

变式1、（2019年博才培圣八上第一次月考）将一张矩形的纸对折，然后用笔尖在上面扎出“”，再把它铺平，你可见到（    ）

A．     B．      C．      D．

变式2、（2018年湘培八上第一次月考）下列图形中，不是轴对称图形的是（    ）

A．         B．          C．          D．

变式3、（2019年北雅八上第一次月考）下列图形中，是轴对称图形的是（    ）

变式4、在日常生活中，你会注意到有一些含有特殊数字规律的车牌号码，如：湘，湘，湘等，这些牌照中的五个数字都是关于中间的一个数字“对称”的，给人以对称美的感受，我们不妨把这样的牌照叫做“数字对称”牌照．如果让你负责制作只以8或9开头且有5个数字的“数字对称”牌照，那么最多可制作_______个．

例3、如图，长方形台球桌ABCD上有两个球P，Q．

（1）请画出一条路径，使得球P撞击台球桌边AB反弹后，正好撞到球Q；

（2）请画出一条路径，使得球P撞击台球桌边，经过两次反弹后，正好撞到球Q；

变式1、如图，弹性小球从点出发，沿所示方向运动，每当小球碰到矩形的边时反弹，反弹时反射角等于入射角，当小球第1次碰到矩形的边时的点为，第2次碰到矩形的边时的点为，，第次碰到矩形的边时的点为，点的坐标是____________．

对应点：折叠后重合的点；

对应线段：折叠后重合的线段；

对应角：折叠后重合的角.

轴对称的基本性质：成轴对称的两个图形中，对应点的连线被对称轴垂直平分，对应线段相等，对应角也相等，且关于直线对称的两个图形全等.

例4、如图，△ABC和△A′B′C′关于直线m对称，

（1）结合图形指出对称点．

（2）找出其中相等的线段和相等的角.

（3）连接A、A′，直线m与线段AA′有什么关系？

变式1、已知，点在内部，点与点关于对称，点与点关于对称，则△是　　

A．含角的直角三角形 B．顶角是的等腰三角形 

C．等边三角形 D．等腰直角三角形

变式2、如图1，是三角形的对称轴，点、是上的两点，若，，则图中阴影部分的面积是_______．

图1                         图2                        图3

变式3、如图2，点关于、的对称点分别为、，连接，交于，交于，若的周长厘米，则为________厘米．

例5、如图3，△ABC和△ABC关于直线MN对称，并且AB＝6，BC＝3，则A'C'的取值范围是___________________．

例6、如图4，点P在∠AOB的内部，点C和点P关于OA对称，点P关于OB对称点是D，连接CD交OA于M，交OB于N．

（1）①若∠AOB＝60°，则∠COD＝_______.；②若∠AOB＝，∠COD        ．

（2）若CD＝4，则△PMN的周长为_____．

图4                           图5                 图6

变式1、如图5，点P为∠AOB内任一点，E，F分别为点P关于OA，OB的对称点．若∠AOB＝30°，则∠E+∠F＝_______°．

变式2、一个等边三角形的对称轴有_______条．

变式3、如图6，△ABC与△A′B′C′关于直线l对称，且∠A＝105°，∠C′＝30°，则∠B的度数为_______°．

1.定义：垂直且平分一条线段的直线，叫做这条线段的垂直平分线.

2.性质：线段垂直平分线上的点到线段两端的距离相等.

3.判定：到线段两端距离相等的点在线段的垂直平分线上.

例7、关于线段的垂直平分线有以下说法：

①一条线段的垂直平分线的垂足，也是这条线段的中点；

②线段的垂直平分线是一条直线；

③一条线段的垂直平分线是这条线段的唯一对称轴；

④线段垂直平分线上的点到线段两个端点的距离相等；

⑤到线段两个端点距离相等的点在线段的垂直平分线上.

其中，正确的说法有（　　）

1.     3个     B. 4个       C. 5个     D. 2个

例8、如图7，直线CD是线段AB的垂直平分线，P为直线CD上一点，若△PAB的周长为14，PA=4，则线段AB的长为______．

图7                       图8                     图9

变式1、如图8，某公园的三个出口、、构成，想要在公园内修建一个公共厕所，要求到三个出口距离都相等．则公共厕所应该在　　

A．三条边的垂直平分线的交点 B．三个角的角平分线的交点 

C．三角形三条高的交点 D．三角形三条中线的交点

变式2、如图9，在中，是边的垂直平分线，，的周长为，则的周长为　　

A．32 B．29 C．38 D．36

变式3、如图10，在中，的平分线与的垂直平分线交于点，连接，若，，则的度数为　　

A． B． C． D．

图10                   图11                            图12

变式4、如图11，在中，点，分别是边上两点，垂直平分，垂直平分，连接，，若，则的大小为　　

A． B． C． D．

变式5、如图12，在中，和的垂直平分线分别交于点、，且点在点的左侧，，则的周长是　　

A． B． C． D．

变式6、如图13，在中，的垂直平分线交于点，交于点，若，，则的周长为　　

A．8 B．11 C．16 D．17

变式7、如图14，为的边的中点，过点作的垂线交于点，连接，若，，则的周长为_______．

图13                         图14                          图15

例9、如图15，点P是∠AOB内任意一点，OP＝10cm，点P关于射线OA对称点为点P1，点P关于射线OB对称点为点P2，连接P1P2，交OA于点C，交OB于点D，当△PCD的周长是10cm时，∠AOB的度数是_______．

变式1、如图15，中，，是上一点，，过点作的垂线交于点，求证：垂直平分．

变式2、如图，已知，，垂直平分交于点，交于．

（1）求的度数；

（2）若，，求的周长．

作图像的对称图像，主要是要找准对称轴，然后利用对称图像的对称性准确画出图像．

若两个图形成轴对称，其对称轴就是任何一对对应点所连线段的垂直平分线．因此只要找到一对对应点，再作出连接它们的线段的垂直平分线就可以得到这两个图形的对称轴．

轴对称图形的对称轴作法相同．

例10、如图是由三个小正方形组成的图形，请你在图中补画一个小正方形，使补画后的图形为轴对称图形，并画出相应的对称轴．

例11、如图16，保持△ABC的三个顶点的横坐标不变，纵坐标都乘﹣1，画出坐标变化后的三角形，则所得三角形与原三角形的关系是（　　）

A．关于x轴对称 

B．关于y轴对称 

C．将原图形沿x轴的负方向平移了1个单位 

D．将原图形沿y轴的负方向平移了1个单位

图16                                    图17

变式1、如图17，在3×3的正方形的网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形，图中的△ABC为格点三角形，在图中最多能画出（　　）个格点三角形与△ABC成轴对称．

A．6个 B．5个 C．4个 D．3个

变式2、(2019年长梅八上第一次月考）在平面直角坐标系中，的三个顶点的位置如图所示

(1)请画出关于轴对称的：(其中、、分别是、、的对应点，不写画法)

(2)直接写出点的坐标_____________；

(3)求的面积

例12、（2019年一中双语八上第一次月考）如图，正方形网格中每个小正方行边长都是1.

（1）画出关于直线对称的图形；

（2）在直线上找一点，使最小（有必要作图痕迹）.

变式1、（2019年一中岳麓八上第一次月考）如图，的顶点都在方格纸中小正方形的顶点上，以小正方形互相垂直的两边所在直线建立平面直角坐标系.

（1）在图中作出关于轴对称的，其中点，，分别和点，，对应；

（2）平移，使得点在轴上，点在轴上，平移后的三角形记为，在图中作出平移后的，其中，，分别和点，，对应，并写出的坐标；

（3）的面积为__________.

变式2、(2019年北雅八上第一次月考）在如图所示的正方形网格中，每个小正方形的边长为1,格点三角形（顶点是网格线的交点的三角形）的顶点的坐标分别为, .

(1) 请在如图所示的网格内作出轴、轴；

(2) 请作出关于轴对称的；

(3) 求出的面积．

1.（2018年长梅八上第一次月考）誉为全国第三大露天碑林的“浯溪碑林”，摩崖上铭刻着多方古今名家碑文，其中悬针篆文具有较高研究价值，下面四个悬针篆文文字明显不是轴对称图形的是（    ）

A     B      C        D

2.（2019年北雅八上第一次月考）以点关于轴对称的点的坐标为（    ）

3.如图18，在3×3的正方形网格中，已有两个小正方形被涂黑，再将图中其余小正方形任意涂黑一个，使整个图案（包括网格）构成一个轴对称图形，则涂色的方法有__   ____种

             图18                图19                        图20

4.(2019年雅境八上第一次月考）如图19，已知正方形的边长为，则图中阴影部分的面积                 ．

5.如图20，四边形ABCD中，AC垂直平分BD，垂足为E，下列结论不一定成立的是（　　）

A. AB=AD       B. AC平分∠BCD        C. AB=BD        D.

6. 如图，已知在Rt△ABC中，∠A=90°，BD是∠ABC的平分线，DE是BC的垂直平分线．试说明BC=2AB．

7.已知，如图，BD是∠ABC的平分线，AB=BC，点P在BD上，PM⊥AD，PN⊥CD，垂足分别是M、N．试说明：PM=PN．

8.（2018年长梅第一次月考）如图，已知、、.

（1）作关于轴对称的；

（2）写出点、、的坐标；

（3）的面积              .

9.如图，BD平分∠ABC交AC于点D，DE⊥AB于E，DF⊥BC于F，AB=6，BC=8，若，求DE的长．

10. 如图，在△ABP中，∠ABP＝60°，，过点A的直线l垂直于线段BP所在的直线．设点B，P关于直线l的对称点分别为点B′，P′

（1）在图1中画出△ABP关于直线l对称的三角形△AB′P′．

（2）若∠BAP＝α，求∠AP′B的度数．（用α表示）

（3）若点P′关于直线AB′的对称点为M，连接AM，PM．请写出PA、PM之间的数量关系和位置关系，并证明你的结论．