初中数学北师大版九年级上册2 用配方法求解一元二次方程优秀课时训练

这是一份初中数学北师大版九年级上册2 用配方法求解一元二次方程优秀课时训练，共9页。
一．选择题


1．把抛物线y＝2x2的图象先向右平移4个单位，再向下平移3个单位所得的解析式为（ ）


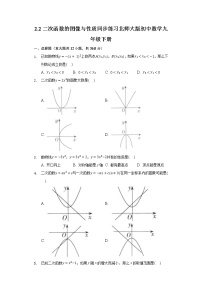
A．y＝2（x﹣3）2+4B．y＝2（x+4）2﹣3


C．y＝2（x﹣4）2﹣3D．y＝2（x﹣4）2+3


2．抛物线y＝（x+）2﹣3的顶点坐标是（ ）


A．（，﹣3）B．（﹣，﹣3）C．（，3）D．（﹣，3）


3．平面直角坐标系中，将抛物线y＝﹣x2先向右平移1个单位，再向上平移2个单位，得到的抛物线的解析式是（ ）


A．y＝（x+1）2+2B．y＝（x﹣1）2+2


C．y＝﹣（x﹣1）2+2D．y＝﹣（x﹣1）2﹣2


4．若A（﹣4，y1），B（﹣1，y2），C（2，y3）在二次函数y＝﹣（x+2）2+3的图象上，则y1，y2，y3的大小关系是（ ）


A．y1＜y2＜y3B．y3＜y1＜y2C．y2＜y1＜y3D．y3＜y2＜y1


5．在同一坐标系中，一次函数y＝mx+n2与二次函数y＝x2+m的图象可能是（ ）


A．B．C．D．


6．下列抛物线中，与抛物线的形状、大小、开口方向都相等的是（ ）


A．B．


C．D．y＝﹣x2+3x﹣5


7．下列关于二次函数y＝2x2+3，下列说法正确的是（ ）


A．它的开口方向向下


B．它的顶点坐标是（2，3）


C．当x＜﹣1时，y随x的增大而增大


D．当x＝0时，y有最小值是3


8．已知二次函数y＝﹣3x2+6x+2，关于该函数在﹣2≤x≤3的取值范围内，下列说法正确的是（ ）


A．有最大值﹣7，最小值﹣22B．有最大值2，最小值﹣22


C．有最大值5，最小值﹣22D．有最大值5，最小值﹣7


9．已知抛物线L：y＝ax2﹣2ax+5（a≠0）的顶点为A，抛物线M与抛物线L关于B（2，0）成中心对称，若抛物线M经过点A，则a的值为（ ）


A．﹣2B．C．﹣5D．


10．如图是二次函数y＝ax2+bx+c图象的一部分，图象过点A（﹣5，0），对称轴为直线x＝﹣2，给出四个结论：①c＞0；②抛物线与轴的另一个交点坐标为（3，0）；③4a﹣b＝0；④若M（﹣3，y1）与N（，y2）是抛物线上两点，则y1＜y2．其中，正确结论的个数是（ ）





A．1B．2C．3D．4


二．填空题


11．如果二次函数的图象与已知二次函数y＝x2﹣2x的图象关于y轴对称，那么这个二次函数的解析式是 ．


12．将抛物线y＝﹣x2﹣2x﹣3向右平移三个单位，再绕原点O旋转180°，则所得抛物线的解析式 ．


13．已知点（2，6），（4，6）是抛物线y＝ax2+bx+c上的两点，则这条抛物线的对称轴是 ．


14．抛物线y＝x2+2x+c顶点在第三象限，则c的取值范围是 ．


15．函数y＝x2﹣2x﹣3（0≤x≤4）的图象如图，直线l∥x轴且过点（0，m），将该函数在直线l上方的图象沿直线l向下翻折，在直线l下方的图象保持不变，得到一个新图象，若新图象对应的函数的最大值与最小值之差不大于5，则m的取值范围是 ．





三．解答题


16．已知抛物线y＝x2﹣mx+2m﹣1过定点H．


（1）求出H的坐标．


（2）若抛物线经过点A（0，1），求证：该抛物线恒在直线y＝﹣2x﹣1上方．


17．（1）画出函数y＝﹣（x﹣1）2+5的图象．


（2）根据图象回答下列问题，该函数的图象是一条 ，对称轴为 ，顶点坐标为 ；有最 值是 ；当 ，y随x的增大而减小．





18．如图，已知抛物线y＝x2﹣（k+1）x+1的顶点A在x轴的负半轴上，且与一次函数y＝﹣x+1交于点B和点C．


（1）求k的值；


（2）求△ABC的面积．








参考答案


1．解：依题意可知，原抛物线顶点坐标为（0，0），


平移后抛物线顶点坐标为（4，﹣3），


又因为平移不改变二次项系数，


所以所得抛物线解析式为：y＝2（x﹣4）2﹣3．


故选：C．


2．解：∵y＝（x+）2﹣3，


∴抛物线y＝（x+）2﹣3的顶点坐标是：（﹣，﹣3）．


故选：B．


3．解：由“左加右减”的原则可知，将抛物线y＝﹣x2先向右平移1个单位所得抛物线的解析式为：y＝﹣（x﹣1）2．


由“上加下减”的原则可知，将抛物线y＝﹣（x﹣1）2向上平移2个单位所得抛物线的解析式为：y＝﹣（x﹣1）2+2；


故选：C．


4．解：∵y＝﹣（x+2）2+3，


∴图象的开口向下，对称轴是直线x＝﹣2，


∵A（﹣4，y1）关于直线x＝﹣2的对称点是（0，y1），


∵﹣1＜0＜2，


∴y3＜y1＜y2，


故选：B．


5．解：A、由直线与y轴的交点在y轴的负半轴上可知，n2＜0，错误；


B、由抛物线的开口向下，错误；


C、由抛物线y轴的交点在y轴的负半轴上可知，m＜0，由直线可知，m＜0，n2＞0，正确；


D、由抛物线y轴的交点在y轴的负半轴上可知，m＜0，由直线可知，m＞0，错误，


故选：C．


6．解：∵抛物线的形状是抛物线，开口向下，


∴抛物线的形状、大小、开口方向都相等的函数的二次项系数是，


故选：B．


7．解：∵二次函数y＝2x2+3，


∴该函数的图象开口向上，故选项A错误；


它的顶点坐标为（0，3），故选项B错误；


当x＜1时，y随x的增大而减小，故选项C错误；


当x＝0时，y取得最小值3，故选项D正确；


故选：D．


8．解：y＝﹣3x2+6x+2＝﹣3（x2﹣2x）+2＝﹣3（x﹣1）2+5，


所以二次函数y＝﹣3x2+6x+2，当x＝1时，y有最大值是5，


∵函数在﹣2≤x≤3的取值范围内，


∴当x＝﹣2时，y＝﹣3x2+6x+2＝﹣3×（﹣2）2+6×（﹣2）+2＝﹣12﹣12+2＝﹣22，


当x＝3时，y＝﹣3x2+6x+2＝﹣3×32+6×3+2＝﹣7，


∴该函数在﹣2≤x≤3的取值范围内的最大值是5，最小值是﹣22，


故选：C．


9．解：∵抛物线L：y＝ax2﹣2ax+5＝a（x﹣1）2+5﹣a，


∴顶点A（1，5﹣a），


∵抛物线M与抛物线L关于B（2，0）成中心对称，


∴抛物线M的开口大小相同，方向相反，顶点为（3，a﹣5）


∴M的解析式是：y＝﹣a（x﹣3）2+a﹣5，


∵抛物线M经过点A，


∴5﹣a＝﹣4a+a﹣5，解得a＝﹣5，


故选：C．


10．解：由函数图象可得，


c＞0，故①正确，


∵二次函数y＝ax2+bx+c的图象过点A（﹣5，0），对称轴为直线x＝﹣2，


∴抛物线与x轴的另一个交点坐标为（1，0），故②错误，


∵对称轴为x＝﹣＝﹣2，得4a﹣b＝0，故③正确，


∵函数图象开口向下，对称轴为直线x＝﹣2，


∴点M（﹣3，y1）比点N（，y2）离对称轴近，


∴y1＞y2，故④错误；


故选：B．


11．解：y＝x2﹣2x的图象关于y轴对称的抛物线x互为相反数，y不变．得y＝（﹣x）2﹣2（﹣x）＝x2+2x．


故答案为y＝x2+2x．


12．解：y＝﹣x2﹣2x﹣3，


＝﹣（x2+2x+1）+1﹣3，


＝﹣（x+1）2﹣2，


所以，抛物线的顶点坐标为（﹣1，﹣2），


∵向右平移三个单位，


∴平移后的抛物线的顶点坐标为（2，﹣2），


∵再绕原点O旋转180°，


∴旋转后的抛物线的顶点坐标为（﹣2，2），


∴所得抛物线解析式为y＝（x+2）2+2，


故答案为y＝（x+2）2+2．


13．解：∵点（2，6），（4，6）是抛物线y＝ax2+bx+c上的两点，


∴这条抛物线的对称轴是x＝＝3，


故答案为：x＝3．


14．解：∵抛物线y＝x2+2x+c＝（x+1）2+c﹣1，


∴抛物线的顶点坐标为（﹣1，c﹣1），


∵抛物线y＝x2+2x+c顶点在第三象限，


∴c﹣1＜0，


解得c＜1，


则c的取值范围是c＜1．


故答案为：c＜1．


15．解：如图1所示，当m等于0时，


∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，


∴顶点坐标为（1，﹣4），


当x＝0时，y＝﹣3，


∴A（0，﹣3），


当x＝4时，y＝5，


∴C（4，5），


∴当m＝0时，


D（4，﹣5），


∴此时最大值为0，最小值为﹣5；


如图2所示，当m＝1时，


此时最小值为﹣4，最大值为1，


当1＜m＜5时，最大值与最小值之差大于5，不合题意；


综上所述：0≤m≤1，


故答案为0≤m≤1．








16．解：（1）∵y＝x2﹣mx+2m﹣1


＝x2﹣4﹣m（x﹣2）+3


＝（x+2）（x﹣2）﹣m（x﹣2）+3


＝（x﹣2）（x+2﹣m）+3，


∴抛物线y＝x2﹣mx+2m﹣1必过定点（2，3），


故H的坐标为（2，3）；





（2）证明：∵抛物线经过点A（0，1），


∴2m﹣1＝1，解得m＝1，


∴抛物线y＝x2﹣x+1，


设y1＝x2﹣x+1，y2＝﹣2x﹣1，


则y1﹣y2＝（x2﹣x+1）﹣（﹣2x﹣1）＝x2+x+2＝（x+）2+＞0，


∴y1＞y2，


∴该抛物线恒在直线y＝﹣2x﹣1上方．


17．解：（1）列表：


描点、连线画出图象如图：


，


（2）由图象可知：该函数的图象是一条抛物线，对称轴为直线x＝1，顶点坐标为（1，5）；有最大值是5；当x＞1，y随x的增大而减小．


故答案为抛物线，直线x＝1，（1，5），大，5，x＞1．


18．解；（1）∵抛物线y＝x2﹣（k+1）x+1的顶点A在x轴的负半轴上，


∴＝0，且﹣＜0，


解得，k＝﹣3；


（2）∵k＝﹣3，


∴抛物线为y＝x2+2x+1，


解x2+2x+1＝﹣x+1得，x1＝0，x2＝﹣3，


∴B（﹣3，4），C（0，1），


由直线y＝﹣x+1可知与x轴的交点D为（1，0），


∵抛物线为y＝x2+2x+1＝（x+1）2，


∴A（﹣1，0），


∴AD＝2，


∴S△ABC＝×2×4﹣＝3．











x
…
﹣1
0
1
2
3
…
y
…
1
4
5
4
1
…