初中数学北师大版九年级上册2 用配方法求解一元二次方程教课ppt课件

这是一份初中数学北师大版九年级上册2 用配方法求解一元二次方程教课ppt课件，共23页。PPT课件主要包含了学习目标，复习引入，配方得，由此可得，二次项系数化为1得，解移项得，x2－3x－1，例1解下列方程，规律总结，k－22＋1等内容，欢迎下载使用。

1.会用配方法解二次项系数不为1的一元二次方程;.（重点）2.能够熟练地、灵活地应用配方法解一元二次方程.（难点）
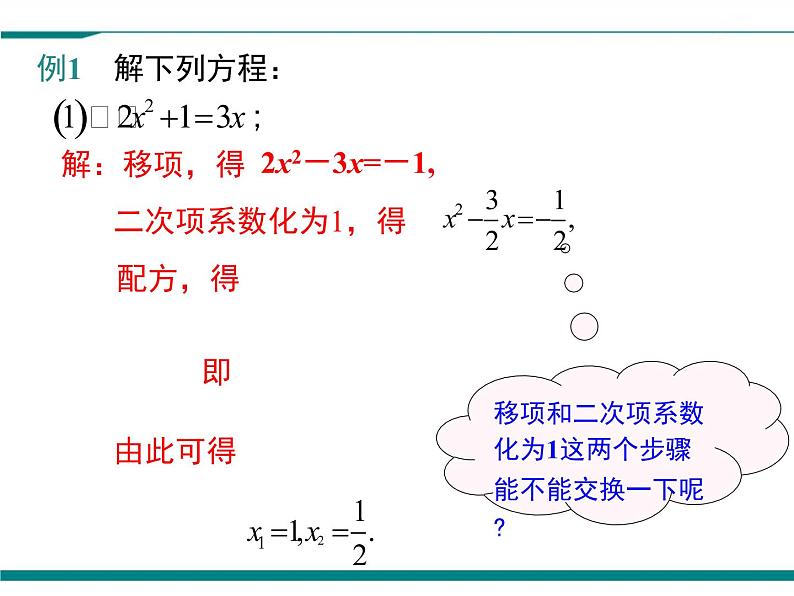
(1) 9x2=1 ；
(2) (x-2)2=2.
2.下列方程能用直接开平方法来解吗?
1.用直接开平方法解下列方程:
(1) x2+6x+9 =5；
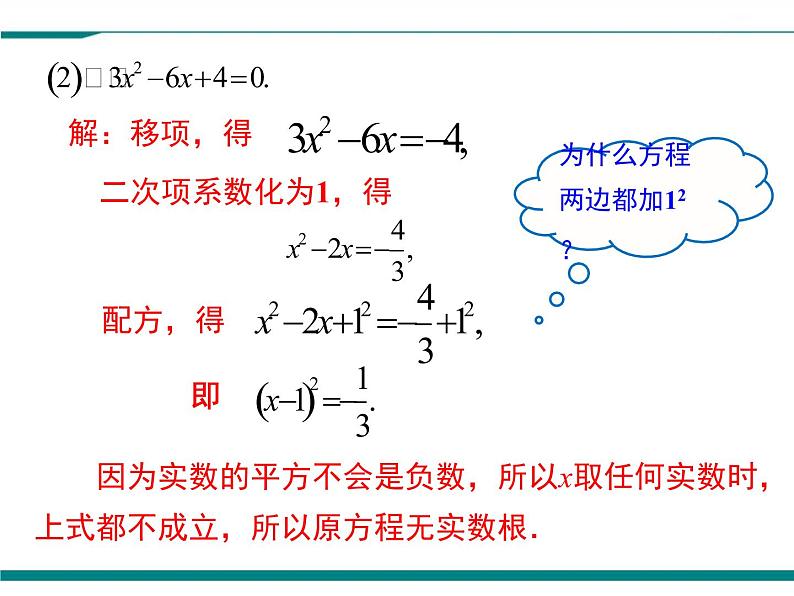
(2)x2+6x+4=0.
把两题转化成(x+n)2=p(p≥0)的形式，再利用开平方
问题1：观察下面两个是一元二次方程的联系和区别： ① x2 + 6x + 8 = 0 ; ② 3x2 +8x－3 = 0.
问题2：用配方法来解 x2 + 6x + 8 = 0 .
解：移项，得 x2 + 6x = -8 , 配方，得 （x + 3）2 = 1. 开平方, 得 x + 3 = ±1. 解得 x1 = -2 , x2= -4.
想一想怎么来解3x2 +8x－3 = 0.
试一试：解方程： 3x2 + 8x -3 = 0. 解：两边同除以3,得 x2 + x - 1=0. 配方,得 x2 + x + ( ) 2 - ( )2 - 1 = 0, （x + ）2 - =0. 移项,得 x + =± , 即 x + = 或 x + = . 所以 x1= , x2 = -3 .
移项和二次项系数化为1这两个步骤能不能交换一下呢?
因为实数的平方不会是负数，所以x取任何实数时，上式都不成立，所以原方程无实数根．
为什么方程两边都加12？
思考1：用配方法解一元二次方程时，移项时要 注意些什么？
思考2：用配方法解一元二次方程的一般步骤.
移项时需注意改变符号.
①移项，二次项系数化为1；②左边配成完全平方式；③左边写成完全平方形式；④降次；⑤解一次方程.
一般地，如果一个一元二次方程通过配方转化成 (x+n)2=p.
①当p>0时,则 ,方程的两个根为②当p=0时,则(x+n)2=0,x+n=0,开平方得方程的两个根为 x1=x2=-n.③当p<0时,则方程(x+n)2=p无实数根.
引例：一个小球从地面上以15m/s的初速度竖直向上弹出，它在空中的高度h (m)与时间 t (s)满足关系：h=15t - 5t2.小球何时能达到10m高？
解：将 h = 10代入方程式中. 15t - 5t2 =10. 两边同时除以-5,得 t2 - 3t = -2, 配方,得 t2 - 3t + ( )2= ( )2 - 2, （t - ）2 =
移项,得 （t - ）2 =即 t - = ,或 t - = .所以 t1= 2 , t2 = 1 .
即在1s或2s时，小球可达10m高.
例2.试用配方法说明：不论k取何实数，多项式 k2－4k＋5 的值必定大于零.
解：k2－4k＋5=k2－4k＋4＋1
因为（k－2）2≥0，所以（k－2）2＋1≥1.
所以k2－4k＋5的值必定大于零.
例3.若a,b,c为△ABC的三边长，且 试判断△ABC的形状.
解：对原式配方，得
由代数式的性质可知
所以，△ABC为直角三角形.
1. 方程2x2 - 3m - x +m2 +2=0有一根为x = 0，则m的值为（ ） A. 1 B.1 C.1或2 D.1或-22.应用配方法求最值.(1) 2x2 - 4x+5的最小值； (2) -3x2 + 5x +1的最大值.
解：原式 = 2(x - 1)2 +3 当x =1时有最小值3
解：原式= -3(x - 2)2 - 4 当x =2时有最大值-4
1.求最值或证明代数式的值为恒正（或负）
对于一个关于x的二次多项式通过配方成a(x+m)2＋n的形式后，(x+m)2≥0，n为常数，当a＞0时，可知其最小值；当a＜0时，可知其最大值.
2.完全平方式中的配方
如：已知x2－2mx＋16是一个完全平方式，所以一次项系数一半的平方等于16，即m2=16，m=±4.
3.利用配方构成非负数和的形式
对于含有多个未知数的二次式的等式，求未知数的值，解题突破口往往是配方成多个完全平方式得其和为0，再根据非负数的和为0，各项均为0，从而求解.如：a2＋b2－4b＋4=0,则a2＋(b－2)2=0,即a=0，b=2.
例4.读诗词解题： （通过列方程，算出周瑜去世时的年龄.） 大江东去浪淘尽， 千古风流数人物。 而立之年督东吴， 早逝英年两位数。 十位恰小个位三， 个位平方与寿符。 哪位学子算得快， 多少年华属周瑜？
解：设个位数字为x，十位数字为(x-3)
x1=6, x2=5
x2-11x+5.52=-30+5.52
(x-5.5)2=0.25
x-5.5=0.5,或x-5.5=-0.5
x2=10(x-3)+x
∴这个两位数为36或25，
∴周瑜去世的年龄为36岁.
∵周瑜30岁还攻打过东吴，
（1）x2+4x-9=2x-11；（2）x(x+4)=8x+12；（3）4x2-6x-3=0； （4） 3x2+6x-9=0.
解：x2+2x+2=0，
解：x2-4x-12=0，
x1=6,x2=-2；
解：x2+2x-3=0，
x1=-3,x2=1.
2.利用配方法证明：不论x取何值，代数式－x2－x－1的值总是负数，并求出它的最大值.
解：－x2－x－1=－(x2+x+ )+ －1
所以－x2－x－1的值必定小于零.
当 时，－x2－x－1有最大值
3.若 ，求(xy)z 的值.
4.如图，在一块长35m、宽26m的矩形地面上，修建同样宽的两条互相垂直的道路，剩余部分栽种花草，要使剩余部分的面积为850m2，道路的宽应为多少？ 
解：设道路的宽为xm, 根据题意得
（35-x)(26-x)=850，
x2-61x+60=0.
x1=60（不合题意，舍去）, x2=1.
5.已知a,b,c为△ABC的三边长，且 试判断△ABC的形状.
所以，△ABC为等边三角形.