
初中数学浙教版九年级下册2.2 切线长定理课后练习题
展开1.切线长定理:过圆外一点,可以引圆的两条切线,切线长________.
2.如图,点P是⊙O外一点,PA,PB切⊙O于点A,B,AB交PO于点C,则有如下结论:
(1)PA=PB;(2)∠APO=∠BPO=∠OAC=∠OBC,∠AOP=∠BOP=∠CAP=∠CBP;(3)AB⊥OP且AC=BC.
A组 基础训练
1.如图,从圆O外一点P引⊙O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB的长是( )
A.4 B.8 C.6 D.10
第1题图
如图,PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中,错误的是( )
第2题图
A.∠1=∠2 B.PA=PB C.AB⊥OP D.PA2=PC·PO
3.如图,一圆内切四边形ABCD,且AB=16,CD=10,则四边形的周长为( )
A.50 B.52 C.54 D.56
第3题图
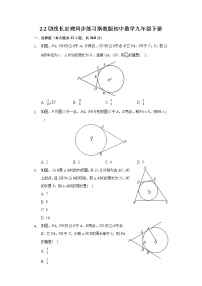
4.(邵阳中考)如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连结BD,AD.若∠ACD=30°,则∠DBA的大小是( )
第4题图
A.15° B.30° C.60° D.75°
5.如图,过⊙O外一点P作⊙O的两条切线PA,PB,切点分别为A,B.下列结论中:①OP垂直平分AB;②∠APB=∠BOP;③△ACP≌△BCP;④PA=AB;⑤若∠APB=80°,则∠OBA=40°.正确的是________.
第5题图
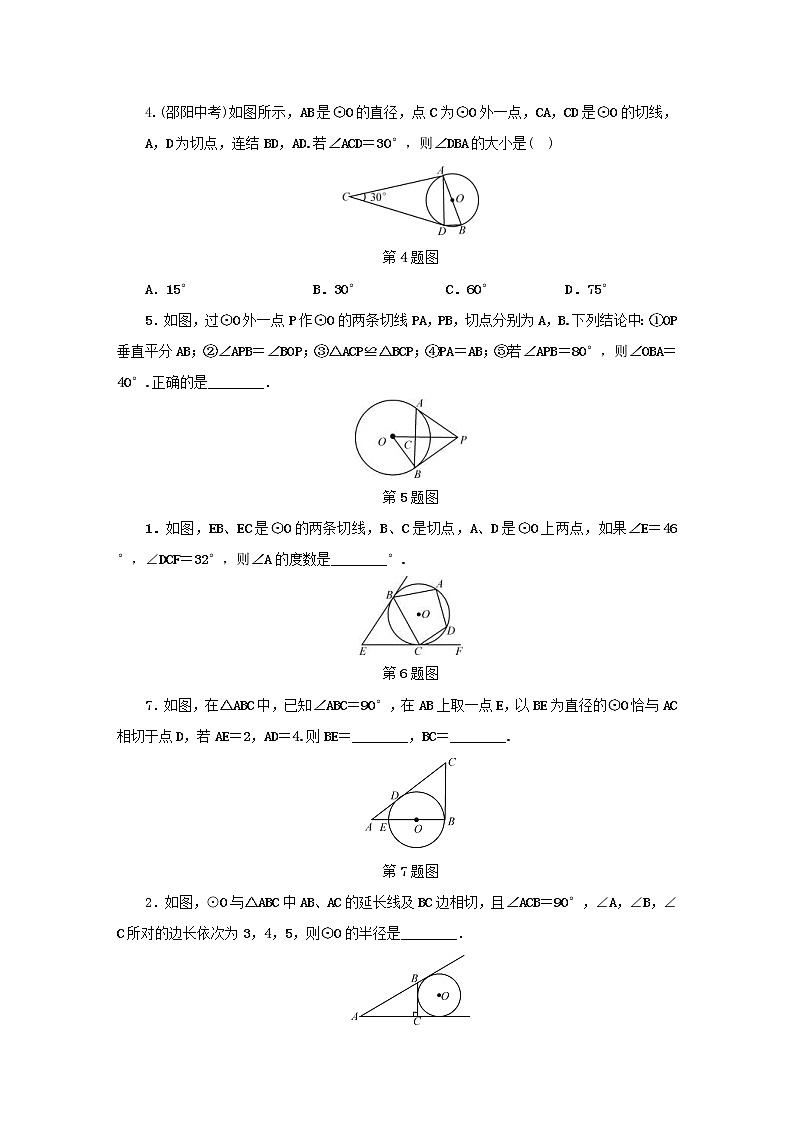
如图,EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是________°.
第6题图
7.如图,在△ABC中,已知∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2,AD=4.则BE=________,BC=________.
第7题图
如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,则⊙O的半径是________.
第8题图
9.如图,AB为半圆O的直径,在AB的同侧作AC,BD切半圆O于点A,B,CD切半圆O于点E.若AC=4,BD=9,求⊙O的半径.
第9题图
10.如图,PA,PB,DE分别切⊙O于点A,B,C,D在PA上,E在PB上.
(1)若PA=30,求△PDE的周长;
(2)若∠P=50°,求∠O的度数.
第10题图
B组 自主提高
11.如图,CA,CD分别切圆O1于A,D两点,CB、CE分别切圆O2于B,E两点,若∠1=60°,∠2=65°,判断AB、CD、CE的长度,下列关系何者正确( )
第11题图
A.AB>CE>CD B.AB=CE>CD C.AB>CD>CE D.AB=CD=CE
12.如图,直尺、三角尺都和⊙O相切,B是切点,且AB=8cm.求⊙O的直径.
第12题图
13.如图,PA,PB分别切⊙O于点A,B,连结PO,AB相交于点D,C是⊙O上一点,∠C=60°.
(1)求∠APB的大小;
(2)若PO=20cm,求△AOB的面积.
第13题图
C组 综合运用
14.如图,在△ABC中,∠B=90°,O是AB上一点,以O为圆心,OB长为半径的圆与AB交于点E,与AC相切于点D,直线ED交BC的延长线于点F.
(1)求证:BC=FC;
(2)若AD∶AE=2∶1,求tanF的值.
第14题图
2.2 切线长定理
【课堂笔记】
1.相等
【课时训练】
1-4.BDBD
①③⑤
99
6 6
2
r=6.法一:可在△COD中,连结OE,有OE2=CE×DE=36,∴r=6.法二:过C作CH⊥BD于点H,在△CDH中,CD=13,DH=5,∴CH=AB=12,即r=6.
(1)∵PA、PB是⊙O切线,∴PA=PB,∵DE是⊙O切线,∴DC=DA,EC=EB,∴△PDE的周长=PD+PE+DC+CE=PD+DA+PE+EB=PA+PB=60; (2)连结AO,BO,CO,可证:∠AOD=∠COD,∠COE=∠BOE,∴∠DOE=eq \f(1,2)∠AOB,∵∠AOB+∠P=180°,∠P=50°,∴∠AOB=130°,∴∠DOE=65°.
A
连结AO,BO,∵AB是⊙O的切线,AC是⊙O的切线,∴∠ABO=90°,∠BAO=eq \f(1,2)∠BAC=60°,在Rt△AOB中,OB=AB·tan∠BAO=8×tan60°=8eq \r(3),∴⊙O的直径为16eq \r(3)cm.
(1)∵PA,PB分别为⊙O的切线,∴OA⊥PA,OB⊥PB,∴∠OAP=∠OBP=90°.∵∠C=60°,∴∠AOB=2∠C=120°,∴在四边形APBO中,∠APB=360°-∠OAP-∠OBP-∠AOB=360°-90°-90°-120°=60°; (2)在Rt△PAO与Rt△PBO中,∵OA=OB,PO=PO,∴Rt△PAO≌Rt△PBO,∴∠APO=∠BPO=eq \f(1,2)∠APB=30°,∴PO⊥AB,∴∠DAO=∠APO=30°,∴OA=sin∠APO×OP=eq \f(1,2)×20=10(cm).在Rt△AOD中,∠DAO=30°,OA=10cm,∴AD=cs∠DAO×OA=eq \f(\r(3),2)×10=5eq \r(3)(cm),OD=sin∠DAO×OA=eq \f(1,2)×10=5(cm),∴AB=2AD=10eq \r(3)(cm),∴S△AOB=eq \f(1,2)AB×OD=eq \f(1,2)×10eq \r(3)×5=25eq \r(3)(cm2).
(1)连结BD.∵BE为⊙O的直径,∴∠BDE=90°,∴∠EBD=90°-∠BED.∵∠EBF=90°,∴∠F=90°-∠BEF.∴∠F=∠EBD.∵AC切⊙O于点D,∴∠EBD=∠ADE=∠CDF.∴∠F=∠CDF,∴DC=FC.∵OB⊥BC,∴BC是⊙O的切线,∴DC=BC.∴BC=FC; (2)在△ADE和△ABD中,∵∠A=∠A,∠ADE=∠ABD,∴△ADE∽△ABD,eq \f(DE,BD)=eq \f(AE,AD)=eq \f(1,2).又∵∠F=∠EBD,∴tanF=tan∠EBD=eq \f(DE,BD)=eq \f(1,2).
初中数学浙教版九年级下册2.2 切线长定理课时训练: 这是一份初中数学浙教版九年级下册2.2 切线长定理课时训练,共10页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
九年级下册第二章 直线与圆的位置关系2.2 切线长定理同步训练题: 这是一份九年级下册第二章 直线与圆的位置关系2.2 切线长定理同步训练题,共10页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2020-2021学年2.2 切线长定理达标测试: 这是一份2020-2021学年2.2 切线长定理达标测试,共4页。