初中数学人教版九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定试讲课课件ppt

这是一份初中数学人教版九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定试讲课课件ppt，共32页。PPT课件主要包含了素养目标，∴∠ADE∠B，符号语言，∠A＝∠A′，ACD，ACB，ADC，勾股定理，即如果，连接中考等内容，欢迎下载使用。

观察两副三角尺如图，其中同样角度（30°与60°，或45°与45°）的两个三角尺大小可能不同，但它们看起来是相似的．一般地，如果两个三角形有两组对应角相等，它们一定相似吗？
1. 掌握“两角对应相等，两个三角形相似”的判定方法.
2. 能够运用三角形相似的条件解决简单的问题.
3. 掌握判定两个直角三角形相似的方法，并能进行相关计算与推理.
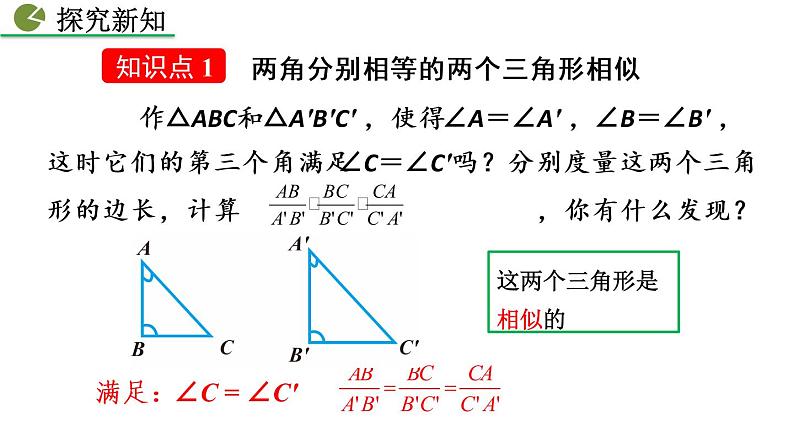
满足：∠C = ∠C'
把你的结果与邻座的同学比较，你们的结论一样吗？ △ABC和△A'B'C'相似吗？
△ABC和△A'B'C'相似
你能试着证明△A′B′C′∽△ABC吗？
如图，已知△ABC和△A'B'C'中，∠A=∠A', ∠B=∠B'，求证: △ABC∽△A'B'C'.
证明：在△ABC的边AB（或延长线）上，截取AD=A'B'，过点D作DE//BC，交AC于点E，则有△ADE∽△ABC.
∵∠ADE=∠B, ∠B=∠B',
又∵∠A=∠A ' ，AD=A'B',
∴△ADE≌△A'B'C'.
∴△A'B'C'∽△ABC.
由此得到利用两组角判定两个三角形相似的定理：两角分别相等的两个三角形相似.
∵ ∠A=∠A'，∠B=∠B'，
∴ △ABC ∽ △A'B'C'.
例1 如图所示，在△ABC和△A′B′C′中，∠B＝∠B′＝90°，∠A＝∠A′，判断这两个三角形是否相似．
解：∵ ∠B＝∠B′＝90°，
∴ △ABC∽△A′B′C′.
例2 弦AB和CD相交于⊙O内一点P,求证:PA·PB=PC·PD.
证明:连接AC、BD.
∵∠A、∠D都是弧CB所对的圆周角,
∴△PAC∽△PDB.
即PA·PB=PC·PD.
∴ .
如图，⊙O 的弦 AB，CD 相交于点 P，若 PA=3， PB = 8，PC = 4，则 PD = .
解：∵ ED⊥AB，∴∠EDA=90°. 又∠C=90 °，∠A=∠A， ∴ △AED ∽△ABC.
如图，在 Rt△ABC 中，∠C = 90°，AB = 10，AC = 8. E 是 AC 上一点，AE = 5，ED⊥AB，垂足为D. 求AD的长.
由此得到一个判定直角三角形相似的方法：有一个锐角相等的两个直角三角形相似.
△ABC∽△A1B1C1.
你能证明吗？可要仔细哟！
Rt△ABC 和 Rt△A1B1C1，
证明：设 ，则AB=kA′B′，AC=kA′C′. 由 ，得 ∴ . ∴ Rt △ABC ∽ Rt △A′B′C′.
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例， 那么这两个直角三角形相似.
判定两直角三角形相似的定理
Rt△ABC 和 Rt△A1B1C1.
解析：∵∠ADC = 90°，AD = 2， ，要使这两个直角三角形相似，有两种情况：（1） 当 Rt△ABC ∽ Rt△ACD 时，有 AC : AD ＝AB : AC， 即 ，解得 AB=3；
（2）当 Rt△ACB ∽ Rt△CDA 时，有 AC : CD ＝AB : AC ， 即 ，解得 ．∴ 当 AB 的长为 3 或 时，这两个直角三角形相似．
如图，在 Rt△ABC 中， ∠ABC = 90°，BD⊥AC于D. 若 AB=6，AD=2，则 AC= ，BD= ，BC= .
1.如图，在△ABC中，点D是边AB上的一点，∠ADC=∠ACB，AD=2，BD=6，则边AC的长为（　　） A．2 B．4 C．6 D．8
2.学校门口的栏杆如图所示，栏杆从水平位置BD绕O点旋转到AC位置，已知AB⊥BD，CD⊥BD，垂足分别为B，D，AO=4m，AB=1.6m，CO=1m，则栏杆C端应下降的垂直距离CD为（　　）A．0.2mB．0.3mC．0.4mD．0.5m
1. 如图，△ABC中，AE 交 BC 于点 D，∠C=∠E，AD : DE=3 : 5，AE=8，BD=4，则DC的长等于（ ）
2. 如图，在 △ABC 和 △A'B'C' 中，若∠A=60°，∠B =40°，∠A' = 60°，当∠C'= 时，△ABC ∽△A'B'C'.
3. 如图，△ABC中，DE∥BC，EF∥AB， 求证：△ADE∽△EFC.
证明: ∵ DE∥BC，EF∥AB，
∠A＝∠FEC.
∴ △ADE∽△EFC.
证明：∵ 在△ ABC中，∠A=40°，∠B=80°， ∴ ∠C=180°－∠A－∠B=60°. ∵ 在△DEF中，∠E=80°，∠F=60°. ∴ ∠B=∠E，∠C=∠F. ∴ △ABC ∽△DEF.
4. 如图，△ABC 和 △DEF 中，∠A=40°，∠B=80°，∠E=80 °，∠F=60 ° ．求证：△ABC ∽△DEF.
证明：∵ △ABC 的高AD、BE交于点F， ∴ ∠FEA=∠FDB=90°， ∠AFE =∠BFD （对顶角相等） ∴ △FEA ∽ △ FDB， ∴
1. 如图，△ABC 的高 AD、BE 交于点 F． 求证：
解：∵ ∠ A= ∠ A,∠ABD=∠C, ∴ △ABD ∽ △ACB , ∴ AB : AC=AD : AB, ∴ AB2 = AD · AC. ∵ AD=2, AC=8, ∴ AB =4.
2.已知:如图,∠ABD=∠C，AD=2, AC=8，求AB.
如图，BE是△ABC的外接圆O的直径，CD是△ABC 的高， 求证：AC · BC = BE · CD.
证明： 连接CE，又∵BE是△ABC的外接圆O的直径， ∴∠BCE= 90°=∠ADC，
∴△ACD∽△EBC.
∵∠A=∠E，∠BCE=∠ADC，
两角分别相等的两个三角形相似
利用两角判定三角形相似