人教版九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定优秀课件ppt

这是一份人教版九年级下册第二十七章 相似27.2 相似三角形27.2.1 相似三角形的判定优秀课件ppt，共31页。PPT课件主要包含了素养目标，符号语言，想一想，图21，图22，相似三角形的判定定理，∠A∠A，∵DEBC，∴DEBF，“A”型等内容，欢迎下载使用。

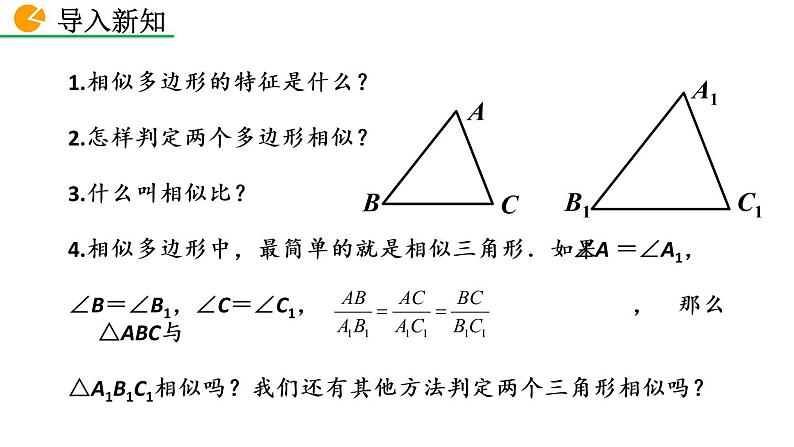
1.相似多边形的特征是什么？2.怎样判定两个多边形相似？3.什么叫相似比？4.相似多边形中，最简单的就是相似三角形．如果∠A ＝∠A1，∠B＝∠B1，∠C＝∠C1， ， 那么△ABC与△A1B1C1相似吗？我们还有其他方法判定两个三角形相似吗？
1. 理解相似三角形的概念，并会用以证明和计算.
2.体会用相似符号“∽”表示的相似三角形之间的边，角对应关系.
3. 掌握平行线分线段成比例的基本事实及其推论的应用，会用平行线判定两个三角形相似并进行证明和计算.
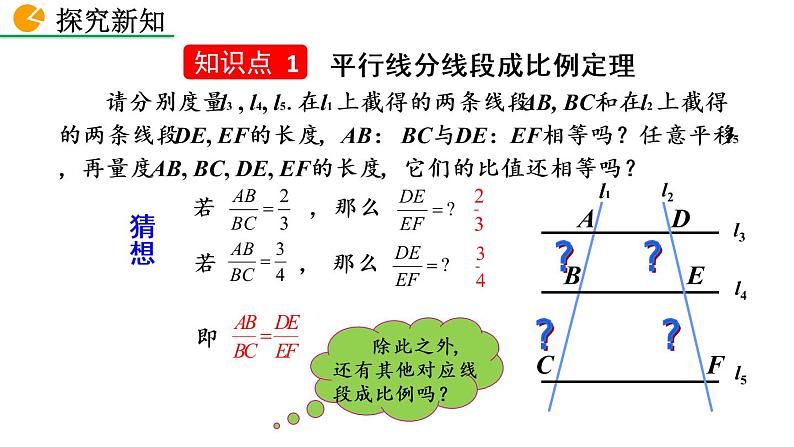
请分别度量l3 , l4, l5.在l1 上截得的两条线段AB, BC和在l2 上截得的两条线段DE, EF的长度, AB： BC与DE：EF相等吗？任意平移l5 , 再量度AB, BC, DE, EF的长度, 它们的比值还相等吗？
平行线分线段成比例定理
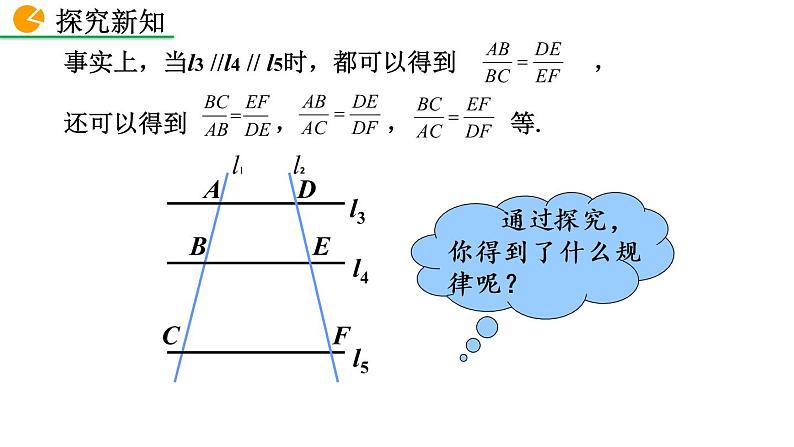
事实上，当l3 //l4 // l5时，都可以得到 ， 还可以得到 ， ， 等.

通过探究，你得到了什么规律呢？
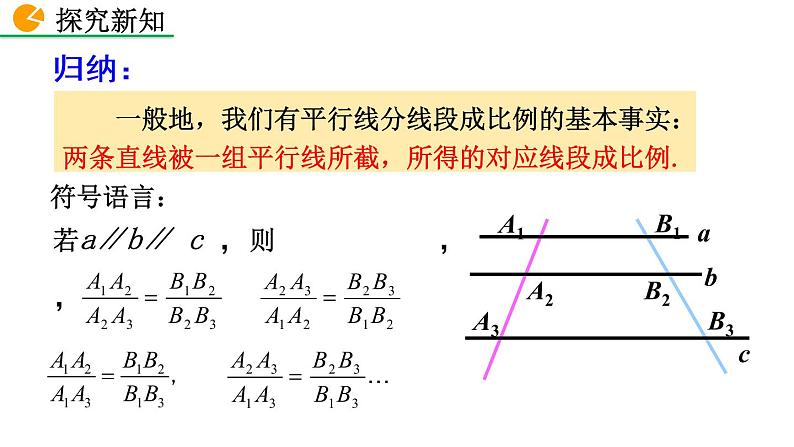
一般地，我们有平行线分线段成比例的基本事实：两条直线被一组平行线所截，所得的对应线段成比例.
若a∥b∥ c ，则 ， ，
1. 如何理解“对应线段”？2.“对应线段”成比例都有哪些表达形式？
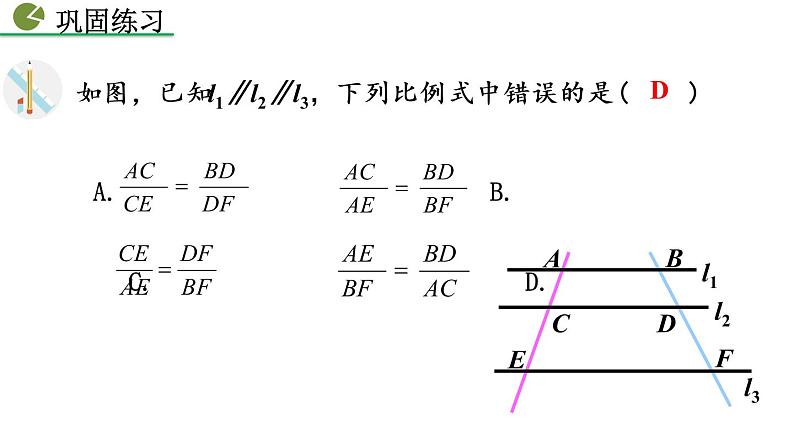
如图，已知l1∥l2∥l3，下列比例式中错误的是 ( ) A. B. C. D.
如图，直线l3∥l4∥l5，由平行线分线段成比例的基本事实，我们可以得出图中对应成比例的线段，
把直线 l1向左或向右任意平移，这些线段依然成比例.
平行线分线段成比例定理的推论
如果把图1中l1 , l2两条直线相交，交点A刚好落到l3上，如图2（1），所得的对应线段的比会相等吗？依据是什么？
【思考】如果把图1中l1 , l2两条直线相交，交点A刚好落到l4上，如图2（2）所得的对应线段的比会相等吗？依据是什么？
平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
解：∵l1∥l2∥l3， ∴ . 又∵ ，DE＝6， ∴ ， 解得EF＝4. ∴DF＝DE＋EF＝6＋4＝10.
例 如图，在△ABC中，DE∥BC，AC=4 ，AB=3，EC=1.求AD和BD.
解：∵AC=4，EC=1，
如图，在△ABC中，EF∥BC，AE=2cm，　BE=6cm，FC=3cm，AF的长为_______．
如图，在△ABC中，D为AB上任意一点，过点D作BC的平行线DE，交AC于点E.问题1 △ADE与△ABC的三个角分别相等吗？问题2 分别度量△ADE与△ABC的边长，它们的边 长是否对应成比例？
问题3 你认为△ADE与△ABC之间有什么关系？平行移动DE的位置，你的结论还成立吗？
通过度量，我们发现△ADE∽△ABC，且只要DE∥BC，这个结论恒成立.
【思考】1.我们通过度量三角形的边长，知道△ADE∽ △ABC，但要用相似的定义去证明它，我们需要证明什么？
2.由前面的结论，我们可以得到什么？还需证明什么？
用相似的定义证明△ADE∽△ABC
证明:在△ADE与△ABC中，
∴∠ADE=∠B, ∠AED=∠C，
过E作EF//AB交BC于F,
∵四边形DBFE是平行四边形,
∴△ADE∽△ABC .
已知：如图，在△ABC中，DE//BC，且DE分别交AB ， AC于点D、E． 求证：△ADE∽△ABC .
定理：平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
符号语言：∵ DE//BC,∴△ADE∽△ABC．
【讨论】过点D作与AC平行的直线与BC相交，可否证明△ADE∽△ABC？如果在三角形中出现一边的平行线，那么你应该联想到什么？
【方法总结】过点D作与AC平行的直线与BC相交，仍可证明△ADE∽△ABC，这与教材第31页证法雷同．题目中有平行线，可得相似三角形，然后利用相似三角形的性质，可列出比例式．
已知：如图，AB∥EF∥CD，图中共有___对相似三角形.
1. 如图，在 △ABC 中，EF∥BC，AE=2cm，BE=6cm，BC = 4 cm，EF 长（ ）
3.如图，在△ABC中， EF∥BC.（ 1 ）如果E、F分别是 AB 和 AC 上的点， AE = BE=7， FC = 4 ，那么 AF 的长是多少？
(2) 如果AB = 10，AE=6，AF = 5，那么 FC 的长是多少？
如图所示，如果D，E，F分别在OA，OB，OC上，且DF∥AC，EF∥BC．求证：OD∶OA＝OE∶OB
证明： ∵ DF∥AC，
如图，已知菱形 ABCD 内接于△AEF，AE=5cm， AF = 4 cm，求菱形的边长.
解：∵ 四边形 ABCD 为菱形，
设菱形的边长为 x cm，则CD = AD = x cm，DF = (4－x ）cm，
两条直线被一组平行线所截，所得的对应线段成比例.
平行于三角形一边的直线截其他两边（或两边延长线），所得的对应线段成比例.
平行于三角形一边的直线与其他两边相交，所构成的三角形与原三角形相似.
平行线分线段成比例定理及其推论