

数学人教版第二十二章 二次函数综合与测试同步测试题
展开一.选择题
1.下列函数中属于二次函数的是( )
A.y=xB.y=2x2﹣1C.y=D.y=x2++1
2.关于二次函数y=﹣2(x+1)2+5,下列说法正确的是( )
A.最小值为5B.最大值为1C.最大值为﹣1D.最大值为5
3.已知关于x的二次函数y=﹣(x﹣m)2+2,当x>1时,y随x的增大而减小,则实数m的取值范围是( )
A.m≤0B.0<m≤1C.m≤1D.m≥1
4.二次函数y=ax2+bx+c的图象如右图所示,若M=5a+4c,N=a+b+c,则( )
A.M>0,N>0B.M>0,N<0C.M<0,N>0D.M<,N<0
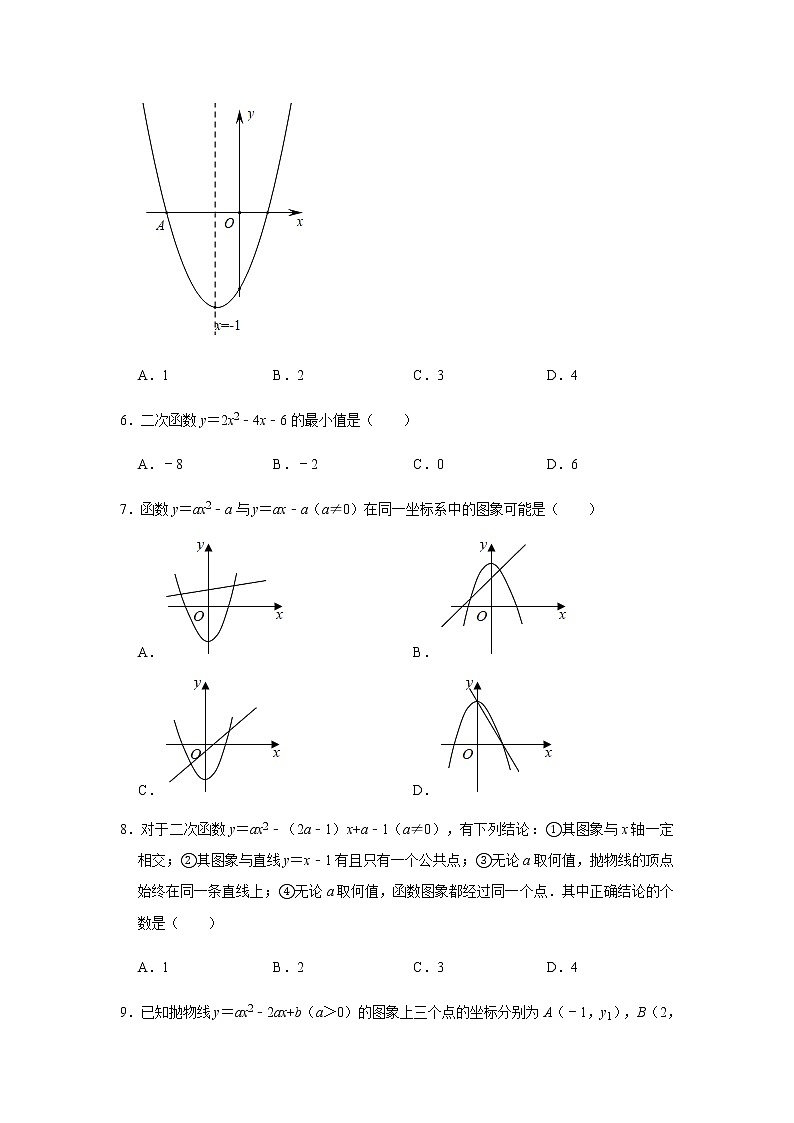
5.如图,二次函数y=ax2+bx+c的图象经过点A(﹣3,0),其对称轴为直线x=﹣1,有下列结论:①abc<0;②a+b+c<0;③5a+4c<0;④4ac﹣b2>0;⑤若P(﹣5,y1),Q(m,y2)是抛物线上两点,且y1>y2,则实数m的取值范围是﹣5<m<3.其中正确结论的个数是( )
A.1B.2C.3D.4
6.二次函数y=2x2﹣4x﹣6的最小值是( )
A.﹣8B.﹣2C.0D.6
7.函数y=ax2﹣a与y=ax﹣a(a≠0)在同一坐标系中的图象可能是( )
A.B.
C.D.
8.对于二次函数y=ax2﹣(2a﹣1)x+a﹣1(a≠0),有下列结论:①其图象与x轴一定相交;②其图象与直线y=x﹣1有且只有一个公共点;③无论a取何值,抛物线的顶点始终在同一条直线上;④无论a取何值,函数图象都经过同一个点.其中正确结论的个数是( )
A.1B.2C.3D.4
9.已知抛物线y=ax2﹣2ax+b(a>0)的图象上三个点的坐标分别为A(﹣1,y1),B(2,y2),C(4,y3),则y1,y2,y3的大小关系为( )
A.y3>y1>y2B.y3>y2>y1C.y2>y1>y3D.y2>y3>y1
10.如图,一段抛物线:y=﹣x(x﹣4)(0≤x≤4)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3…如此变换进行下去,若点P(21,m)在这种连续变换的图象上,则m的值为( )
A.2B.﹣2C.﹣3D.3
二.填空题
11.抛物线y=ax2﹣2ax﹣3与x轴交于两点,分别是(x1,0),(x2,0),则x1+x2= .
12.二次函数y=x2﹣3x+2的图象与x轴的交点坐标是 .
13.如图,二次函数y=ax2+bx+c的图象经过(﹣1,0)(3,0)两点,给出的下列6个结论:
①ab<0;
②方程ax2+bx+c=0的根为x1=﹣1,x2=3;
③4a+2b+c<0;
④当x>1时,y随x值的增大而增大;
⑤当y>0时,﹣1<x<3;
⑥3a+2c<0.
其中不正确的有 .
14.某幢建筑物,从5米高的窗口A用水管向外喷水,喷的水流呈抛物线,抛物线所在平面与墙面垂直(如图所示),如果抛物线的最高点M离墙1米,离地面米,则水流下落点B离墙距离OB是 m.
15.二次函数y=ax2+bx+1(a≠0)的图象与x轴有两个交点A,B,顶点为C.若△ABC恰好是等边三角形,则代数式b2﹣2(2a﹣5)= .
三.解答题
16.已知二次函数y=ax2+bx+c(a≠0)的顶点坐标为P(h,k),h≠0.
(1)若该函数图象过点(2,1),(5,7),h=3.
①求该函数解析式;
②t≤x0≤t+1,函数图象上点Q(x0,y0)到x轴的距离最小值为1,则t的值为 ;
(2)若点P在函数y=x2﹣3x+c的图象上,且≤a≤2,求h的最大值.
17.已知二次函数的解析式是y=x2﹣2x﹣3.
(1)把它变形为y=a(x﹣h)2+k的形式: ;
(2)它的顶点坐标是 ;当x 时,y随x的增大而减小.
(3)在坐标系中利用描点法画出此抛物线;
(4)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .
18.“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行,某自行车店在销售某型号自行车时,标价1500元.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价是多少元?
(2)若该型号自行车的进价不变,按标价出售,该店平均每月可售出60辆;若每辆自行车每降价50元,每月可多售出10辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
19.阅读以下材料:
对于三个数a、b、c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{﹣1,2,3}==;min{﹣1,2,3}=﹣1,…解决下列问题:
(1)填空:如果min{2,2x+2,4﹣2x}=2,则x的取值范围为 ;
(2)①如果M{2,x+1,2x}=min{2,x+1,2x},求x;
②根据①,你发现了结论:如果M{a,b,c}=min{a,b,c},那么 (填a、b、c的大小关系),证明你发现的结论.
③运用②的结论,填空:若M{2x+y+2,x+2y,2x﹣y}=min{2x+y+2,x+2y,+2x﹣y},则x+y
(3)在同一直角坐标系中作出函数y=x+1,y=(x﹣1)2,y=2﹣x的图象(不需列表描点),通过观察图象,填空:min{x+1,(x﹣1)2,2﹣x}的最大值为 .
20.在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过A(0,﹣4)和B(2,0)两点.
(1)求c的值及a,b满足的关系式;
(2)若抛物线在A和B两点间,y随x的增大而增大,求a的取值范围;
(3)抛物线同时经过两个不同的点M(p,m),N(﹣2﹣p,n).
①若m=n,求a的值;
②若m=﹣2p﹣3,n=2p+1,点M在直线y=﹣2x﹣3上,请验证点N也在y=﹣2x﹣3上并求a的值.
参考答案
一.选择题
1.解:A、y=x是正比例函数,故本选项不符合题意;
B、y=2x2﹣1是二次函数,故本选项符合题意;
C、y=不是二次函数,故本选项不符合题意;
D、y=x2++1不是二次函数,故本选项不符合题意.
故选:B.
2.解:∵二次函数y=﹣2(x+1)2+5,
可得函数开口向下,
∴函数有最大值,
∴当x=﹣1时,函数有最大值5,
故选:D.
3.解:∵函数的对称轴为x=m,
又∵二次函数开口向下,
∴在对称轴的右侧y随x的增大而减小,
∵x>1时,y随x的增大而减小,
∴m≤1.
故选:C.
4.解:∵当x=2.5时,y=a+b+c>0,
∴25a+10b+4c>0,
∵﹣=1,
∴b=﹣2a,
∴25a﹣20a+4c>0,即5a+4c>0,
∴M>0,
∵当x=1时,y=a+b+c>0,
∴N>0,
故选:A.
5.解:①观察图象可知:
a>0,b>0,c<0,∴abc<0,
∴①正确;
②当x=1时,y=0,即a+b+c=0,
∴②错误;
③对称轴x=﹣1,即﹣=﹣1
得b=2a,
当x=时,y<0,
即a+b+c<0,
即a+2b+4c<0,
∴5a+4c<0.
∴③正确;
④因为抛物线与x轴有两个交点,
所以△>0,即b2﹣4ac>0,
∴4ac﹣b2<0.
∴④错误;
⑤∵(﹣5,y1)关于直线x=﹣1的对称点的坐标是(3,y1),
∴当y1>y2时,﹣5<m<3.
∴⑤正确.
故选:C.
6.解:y=2x2﹣4x﹣6=2(x﹣1)2﹣8,
因为图象开口向上,故二次函数的最小值为﹣8.
故选:A.
7.解:①当a>0时,二次函数y=ax2﹣a的图象开口向上、对称轴为y轴、顶点在y轴负半轴,一次函数y=ax﹣a(a≠0)的图象经过第一、三、四象限,且两个函数的图象交于y轴同一点;
②当a<0时,二次函数y=ax2﹣a的图象开口向下、对称轴为y轴、顶点在y轴正半轴,一次函数y=ax﹣a(a≠0)的图象经过第一、二、四象限,且两个函数的图象交于y轴同一点.
对照四个选项可知D正确.
故选:D.
8.解:①当y=0,ax2﹣(2a﹣1)x+a﹣1=0,
解得x1=1,x2=,
则二次函数y=ax2﹣(2a﹣1)x+a﹣1的图象与x轴的交点坐标为(1,0)、(,0),
故①正确,符合题意;
②由题意得:ax2﹣(2a﹣1)x+a﹣1=x﹣1,化简得:x2﹣2x+1=0,
△=22﹣4=0,故抛物线图象与直线y=x﹣1有且只有一个公共点,
故②正确,符合题意;
③该抛物线对称轴为x=1﹣,顶点的纵坐标为y=,
则y=(1﹣)﹣,即无论a取何值,抛物线的顶点始终在直线y=x﹣上,
所以③正确,符合题意;
④由①知,二次函数y=ax2﹣(2a﹣1)x+a﹣1的图象与x轴的交点坐标为(1,0)、(,0),
故无论a取何值,函数图象都经过同一个点(1,0),故④正确,符合题意.
故选:D.
9.解:y=ax2﹣2ax+b(a>0),
对称轴是直线x=﹣=1,
即二次函数的开口向上,对称轴是直线x=1,
即在对称轴的右侧y随x的增大而增大,
A点关于直线x=1的对称点是D(3,y1),
∵2<3<4,
∴y3>y1>y2,
故选:A.
10.解:∵y=﹣x(x﹣4)(0≤x≤4)记为C1,它与x轴交于两点O,A1,
∴点A1(4,0),
∴OA1=4,
∵OA1=A1A2=A2A3=A3A4,
∴OA1=A1A2=A2A3=A3A4=4,
∵点P(21,m)在这种连续变换的图象上,
∴x=21和x=1时的函数值互为相反数,
∴﹣m=﹣1×(1﹣4)=3,
∴m=﹣3,
故选:C.
二.填空题(共5小题)
11.解:由韦达定理得:
x1+x2=﹣=2,
故答案为2.
12.解:当y=0时,x2﹣3x+2=0,
解得x1=1,x2=2,
所以二次函数y=x2﹣3x+2x的图象与x轴的交点坐标是(1,0),(2,0).
故答案为(1,0)、(2,0).
13.解:①∵抛物线开口向上,对称轴在y轴右侧,与y轴交于负半轴,
∴a>0,﹣>0,c<0,
∴b<0,
∴ab<0,说法①正确;
②二次函数y=ax2+bx+c的图象经过(﹣1,0)(3,0)两点,
∴方程ax2+bx+c=0的根为x1=﹣1,x2=3,说法②正确;
③∵当x=2时,函数y<0,
∴4a+2b+c<0,说法③正确;
④∵抛物线与x轴交于(﹣1,0)、(3,0)两点,
∴抛物线的对称轴为直线x=1,
∵图象开口向上,
∴当x>1时,y随x值的增大而增大,说法④正确;
⑤∵抛物线与x轴交于(﹣1,0)、(3,0)两点,且图象开口向上,
∴当y<0时,﹣1<x<3,说法⑤错误;
⑥∵当x=﹣1时,y=0,
∴a﹣b+c=0,
∴抛物线的对称轴为直线x=1=﹣,
∴b=﹣2a,
∴3a+c=0,
∵c<0,
∴3a+2c<0,说法⑥正确.
故答案为⑤.
14.解:地面,墙面所在直线为x轴,y轴建立平面直角坐标系,
设抛物线解析式:y=a(x﹣1)2+,
把点A(0,5)代入抛物线解析式得:
a=﹣,
∴抛物线解析式:
y=﹣(x﹣1)2+.
当y=0时,x1=﹣1(舍去),x2=3.
∴OB=3(m).
故答案为3.
15.解:如图,过C作CE⊥AB于E.
当△ABC等边三角形时,CE=AC•sin60°=AC=AB,
令y=ax2+bx+1=0,解得x=,
则AB==,
而CE=﹣,
即==×,
∵b2﹣4a>0,
故b2﹣4a=12.
则b2﹣2(2a﹣5)=b2﹣4a+10=22,
故答案是22.
三.解答题(共5小题)
16.解:(1)①设解析式为y=a(x﹣h)2+k,
将(2,1),(5,7),h=3代入,得
解得a=2,k=﹣1,
所以,解析式为y=2(x﹣3)2﹣1,即y=2x2﹣12x+17,
②把y=1代入y=2x2﹣12x+17求得x=2或4,
把y=﹣1代入y=2x2﹣12x+17求得x=3,
∵t≤x0≤t+1,函数图象上点Q(x0,y0)到x轴的距离最小值为1,
∴t=1或t=4,
故答案为t=1或t=4.
(2)设解析式为y=a(x﹣h)2+k,由y=ax2+bx+c(a≠0)知图象过(0,c),
∴c=ah2+k.
∵点P在函数y=x2﹣3x+c的图象上,
∴k=h2﹣3h+c,
∴h2﹣3h+ah2=0,
∵h≠0,
∴,
∵,h随a的增大而减小,
∴当时,h的值最大,h的最大值为2.
17.解:(1)y=x2﹣2x﹣3=(x﹣1)2﹣4,
故答案为y=(x﹣1)2﹣4;
(2)抛物线的顶点坐标为(1,﹣4),当x<1时,y随x的增大而减小.
故答案为(1,﹣4),<1;
(3)列表:
描点,连线画出函数图象如图:
(3)当﹣2<x<2时,函数值y的取值范围是﹣4≤y<5,
故答案为﹣4≤y<5.
18.解:(1)设进价为x元,
则由题意得:(1500×0.9﹣x)×8=(1500﹣100﹣x)×7,
解得:x=1000,
∴改型号自行车进价1000元;
(2)设自行车降价x元,获利为y元,
则:==,
∴对称轴:x=100,
∵,
∴当x=100时,=32000,
答:降价100元时每月利润最大,最大利润为32000元.
19.解:(1)由min{2,2x+2,4﹣2x}=2,得,即0≤x≤1,
故答案为:0≤x≤1;
(2)①∵M{2,x+1,2x}=min{2,x+1,2x},
∴,解得:,
∴x=1;
②证明:由M{a,b,c}=min{a,b,c},可令=a,即b+c=2a;
又∵,
解之得:a+c≤2b,a+b≤2c;
把b+c=2a代入a+c≤2b 可得c≤b;把b+c=2a代入a+b≤2c可得b≤c;
∴b=c;将b=c代入b+c=2a得c=a;
∴a=b=c,
故答案为:a=b=c;
③据②可得,
解之得y=﹣1,x=﹣3,
∴x+y=﹣4,
故答案为:=﹣4;
(3)作出图象,由图可知min{x+1,(x﹣1)2,2﹣x}的最大值为1,
故答案为:1.
20.解:(1)令x=0,则c=﹣4,
将点B(2,0)代入y=ax2+bx+c可得4a+2b﹣4=0,
∴2a+b=2;
(2)当a>0时,
∵A(0,﹣4)和B(2,0),
∴对称轴x=﹣=﹣=1﹣≤0,
∴0<a≤1;
当a<0时,
对称轴x=1﹣≥2,
∴﹣1≤a<0;
综上所述:﹣1≤a≤1且a≠0;
(3)①当m=n时,M(p,m),N(﹣2﹣p,n)关于对称轴对称,
∴对称轴x=1﹣=﹣1,
∴a=;
②将点N(﹣2﹣p,n)代入y=﹣2x﹣3,
∴n=4+2p﹣3=1+2p,
∴N点在y=﹣2x﹣3上,
联立y=﹣2x﹣3与y=ax2+(2﹣2a)x﹣4有两个不同的实数根,
∴ax2+(4﹣2a)x﹣1=0,
∵p+(﹣2﹣p)=,
∴a=1.
x
…
…
y
…
…
x
…
﹣1
0
1
2
3
…
y
…
0
﹣3
﹣4
﹣3
0
…
九年级上册数学月考训练题(一): 这是一份九年级上册数学月考训练题(一),共16页。试卷主要包含了下列方程中,一元二次方程共有个,若实数x满足方程等内容,欢迎下载使用。
九年级上册数学月考训练题(二): 这是一份九年级上册数学月考训练题(二),共10页。试卷主要包含了若关于x的一元二次方程,平移抛物线y=,已知二次函数y=等内容,欢迎下载使用。
数学九年级上册第二十四章 圆综合与测试精品综合训练题: 这是一份数学九年级上册第二十四章 圆综合与测试精品综合训练题,共23页。













