第22章 二次函数小结第2课时 专题一 二次函数的图象与性质-2024-2025学年九年级数学上册教材配套同步课件（人教版）

这是一份第22章 二次函数小结第2课时 专题一 二次函数的图象与性质-2024-2025学年九年级数学上册教材配套同步课件（人教版），共23页。

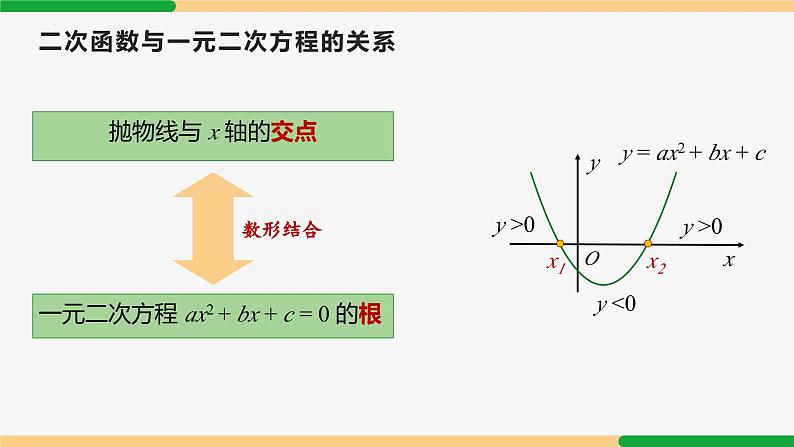
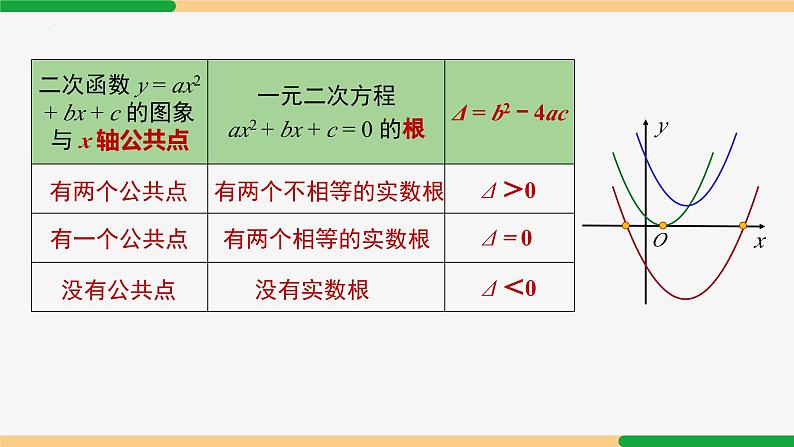
二次函数的图象与性质第22章 小结与复习| 第2课时|专题内容专题四：二次函数与一元二次不等式的关系 专题二：二次函数的增减性问题专题五：二次函数图像与系数 a，b，c 之间关系 专题三：二次函数与一元一次方程的关系专题一：二次函数的平移关系专题一：二次函数的平移关系例1. 若抛物线 y =－7(x + 4)2－1 平移得到 y =－7x2，则可以（ ）A. 先向左平移 4 个单位，再向下平移 1 个单位B. 先向右平移 4 个单位，再向上平移 1 个单位C. 先向左平移 1 个单位，再向下平移 4 个单位D. 先向右平移 1 个单位，再向下平移 4 个单位B专题二：二次函数的增减性问题例2. 已知 (-3，y1)，(-2，y2)， (1，y3) 是抛物线 y = 4x2 上的点，则( )A．y1＜y2＜y3 B．y3＜y1＜y2 C．y3＜y2＜y1 D．y2＜y3＜y1C若开口向上，则距离越大，其纵坐标越大；若开口向下，则距离越大，其纵坐标越小．专题三：二次函数与一元一次方程的关系例3. 二次函数 y = ax2 + bx + c (a ≠ 0) 的图象如图所示，则方程 ax2 + bx + c − 2 = 0 的根的情况是(　　)A．有两个相等的实数根B．有两个不相等的实数根C．没有实数根D．以上都不正确B例4. 如图，二次函数 y = x2 - 3x - 4 与一次函数 y = x - 4 交于 A、B 两点，则 A、B 两点坐标是多少？解：得 x2 - 3x - 4 = x - 4 ∴ x1 = 0， x2 = 4 ∴ A(0，-4)，B(4，0).二次函数与一元二次方程的关系抛物线与 x 轴的交点一元二次方程 ax2 + bx + c = 0 的根数形结合 y = ax2 + bx + cx1x2 y >0 y >0 y <0有两个公共点有两个不相等的实数根Δ ＞0有一个公共点有两个相等的实数根Δ = 0没有公共点没有实数根Δ ＜0专题四：二次函数与一元二次不等式的关系 例5.函数 y = ax2 + bx+ c 的图象如图，那么方程 ax2 + bx + c = 0 的根是______________；不等式 ax2 + bx + c > 0 的解集是______________；不等式 ax2 + bx + c < 0 的解集是____________.x1 = −1，x2 = 3x < −1 或 x > 3−1 < x < 3例6.函数 y = ax2 + bx + c 的图象如图，那么方程 ax2 + bx + c = 2 的根是______________；不等式 ax2 + bx + c > 2 的解集是______________；不等式 ax2 + bx + c < 2 的解集是____________.x1 = −2，x2 = 4x < −2 或 x > 4−2 < x < 4(4, 2)(−2, 2) y = ax² + bx + c a＞0y＜0，x1＜x＜x2；y＞0，x＜x1 或 x＞x2.y＞0，x≠ x0 y＜0，无解.y＞0，所有实数；y＜0，无解. y = ax² + bx + c a<0y＜0，x＜x1 或 x＞x2y＞0，x1＜x＜x2；.y＞0，无解. y＜0，x≠ x0y＞0，无解；y＜0，所有实数.专题五：二次函数图像与系数 a，b，c 之间关系 例7. 已知二次函数 y＝ax2 ＋ bx ＋ c 的图象如图所示，下列结论：①abc＞0；②2a－b＜0；③4a－2b＋c＜0；④(a＋c)2＜b2. 其中正确的个数是 (　　)A．1　　　B．2　　　　C．3　　　D．4①③④ 都正确. 故选 C. C例8.抛物线 y＝ax2＋bx＋c 的对称轴是直线 x = -1，其图象如图所示．下列结论：① abc＜0；② (4a＋c)2＜(2b)2；③若 (x1，y1) 和 (x2，y2) 是抛物线上的两点，则当 | x1＋1|＞| x2＋1| 时，y1＜y2；④抛物线的顶点坐标为(-1，m)，则关于 x 的方程 ax2＋bx＋c ＝m - 1 无实数根．其中正确结论的个数是(　　) A．4　　　B．3　　　C．2　　　D．1①②④ 正确，故选：B. B对于二次函数 y＝ax2 ＋ bx ＋ c (a ≠ 0) ，(1) 二次项系数 a 决定抛物线的开口方向和大小． 当 a＞0时，抛物线向上开口； 当 a＜0时，抛物线向下开口；(2) 一次项系数 b 和二次项系数 a 共同决定对称轴的位置. 当 a 与 b 同号时(即 ab＞0)，对称轴在 y 轴左； 当 a与 b 异号时(即 ab＜0)，对称轴在 y 轴右；(3) 常数项 c 决定抛物线与 y 轴交点位置．二次函数图象与系数的关系课堂练习1. 关于抛物线 y = −x2 + 2x − 3 的判断，下列说法正确的是 (　　)A．抛物线的开口方向向上B．抛物线的对称轴是直线 x = -1C．抛物线对称轴左侧部分从左往右是下降的D．抛物线顶点到 x 轴的距离是 2D2. 已知二次函数 y =－x2＋2bx＋c，当 x＞1 时，y 的值随 x 值的增大而减小，则实数 b 的取值范围是 ( ) A. b≥－1 B. b≤－1 C. b≥1 D. b≤1D3. 抛物线 y = 2x2 − 4x 上三点分别为 (−3，y1)，(0，y2)， (3，y3) ，则 y1，y2，y3 的大小关系为_____________(用“＞”号连接)y1＞y3＞y24. 已知点 (−1，y1)，(1.5，y2)，(2，y3) 在函数 y = ax2 − 2ax + a − 2 (a＞0) 的图象上，则将 y1、y2、y3 按由大到小的顺序排列是 (　　)A．y1＞y2＞y3 B．y1＞y3＞y2C．y2＞y1＞y3 D．y3＞y2＞y1 B5. 二次函数 y = x2 - x - 2 的图象如图所示，则函数值 y＞0 时，x 的取值范围是( )A．x＜-1 B．x＞2C．-1＜x＜2 D．x＜-1 或 x＞2D6. 如图，抛物线 y = ax2 与直线 y = bx + c 的两个交点坐标分别为 A(-2，4)，B(1，1)，则关于 x 的方程 ax2 - bx - c = 0 的解为________________. x1 = -2，x2 = 1 如图，若二次函数 y = ax2 (a≠0) 与直线 y = bx + c(b≠0) 的两个交点坐标 A(-1，1)，B(2，4). 则使得关于 x 的不等式 ax2＜bx + c 成立的 x 的取值范围是_________.-1＜x＜2 B如图，二次函数 y＝ax2＋bx＋c (a≠0) 图象的一部分与 x 轴的一个交点坐标为(1，0)，对称轴为 x = -1，结合图象给出下列结论：① a + b + c = 0； ② a - 2b + c＜0；③关于 x 的一元二次方程 a2 + bx + c = 0 (a≠0) 的两根分别为 -3 和 1；④若点( -4，y1)，(-2，y2)，(3，y3) 均在二次函数图象上，则 y1＜y2＜y3；⑤ a - b＜m(am + b) (m 为任意实数).其中正确结论的个数是(　　) A．1　　　B．2　　　　C．3　　　D．4综上 ①②③ 正确C如图，已知抛物线 y = ax2 + bx + c 经过 A (−1，0)、B (3，0) 两点，与 y 轴交于点 C(0，−3)．(1) 求二次函数的解析式；(2) 点 Q 为抛物线上一点，若 S△QAB = 8，求出此时点 Q 的坐标．(1) 解：设二次函数解析式为 y = a(x + 1)(x − 3)，将点(0，−3)代入，得−3 = a(0 + 1)(0 − 3).解得 a = 1.∴二次函数的解析式为 y = (x + 1)(x − 3) = x2 − 2x − 3.(2) 点 Q 为抛物线上一点，若 S△QAB = 8，求出此时点 Q 的坐标．解：设 Q (x，y)，∴ y = ±4．② 当 y = -4 时，即 x2 − 2x − 3 = −4.解得 x3 = x4 = 1.则 Q 点的坐标为(1，−4).① 当 y = 4 时，即 x2 − 2x − 3 = 4.