数学八年级上册第一章 勾股定理2 一定是直角三角形吗优秀ppt课件

这是一份数学八年级上册第一章 勾股定理2 一定是直角三角形吗优秀ppt课件，共25页。PPT课件主要包含了学习目标，勾股定理的逆定理，特别说明，常见勾股数，勾股数拓展性质等内容，欢迎下载使用。

1.了解直角三角形的判定条件．（重点）2.能够运用勾股数解决简单实际问题． （难点）
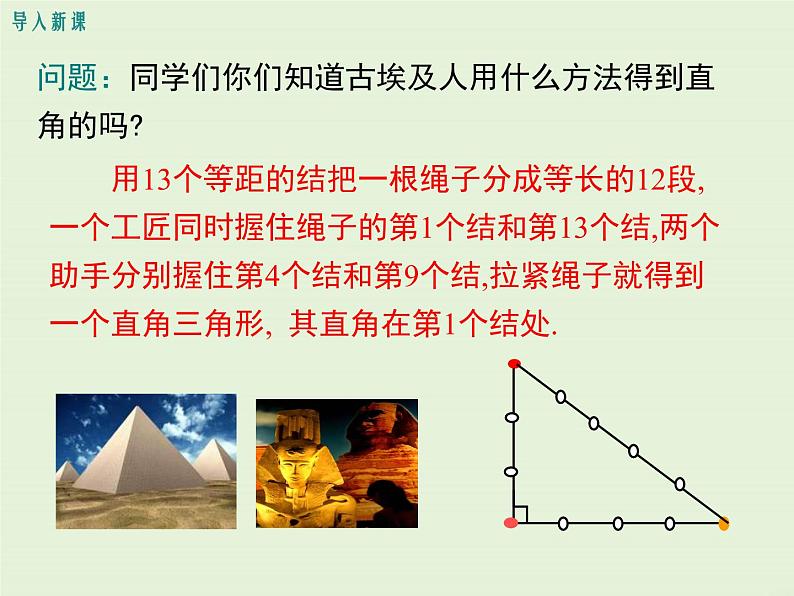
问题：同学们你们知道古埃及人用什么方法得到直角的吗?
用13个等距的结把一根绳子分成等长的12段,一个工匠同时握住绳子的第1个结和第13个结,两个助手分别握住第4个结和第9个结,拉紧绳子就得到一个直角三角形, 其直角在第1个结处.
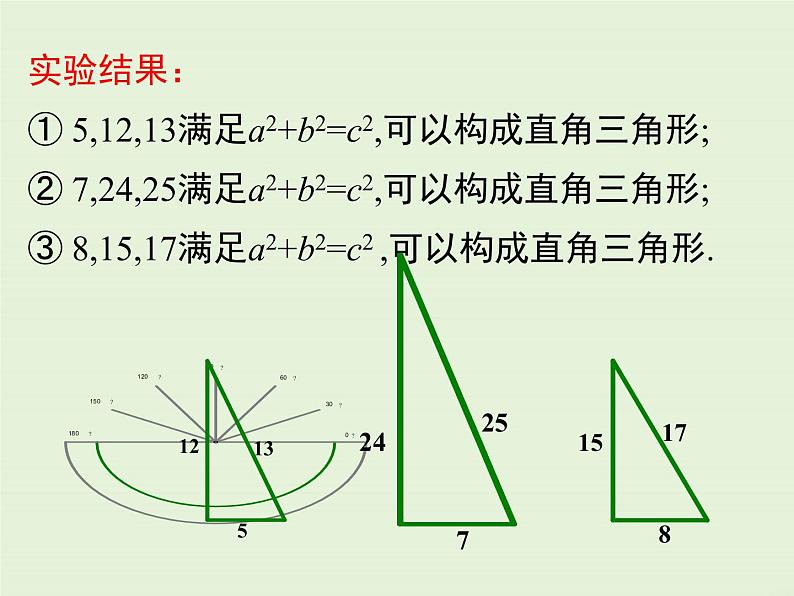
探究：下面有三组数分别是一个三角形的三边长a, b, c: ①5,12,13; ②7,24,25; ③8,15,17.回答下列问题:1.这三组数都满足 a2+b2=c2吗？2.分别以每组数为三边长作出三角形，用量角器量一量，它们都是直角三角形吗？
实验结果： ① 5,12,13满足a2+b2=c2,可以构成直角三角形;② 7,24,25满足a2+b2=c2,可以构成直角三角形;③ 8,15,17满足a2+b2=c2 ,可以构成直角三角形.
思考：从上述问题中，能发现什么结论吗？
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
有同学认为测量结果可能有误差,不同意 这个发现.你觉得这个发现正确吗?你能给 出一个更有说服力的理由吗?
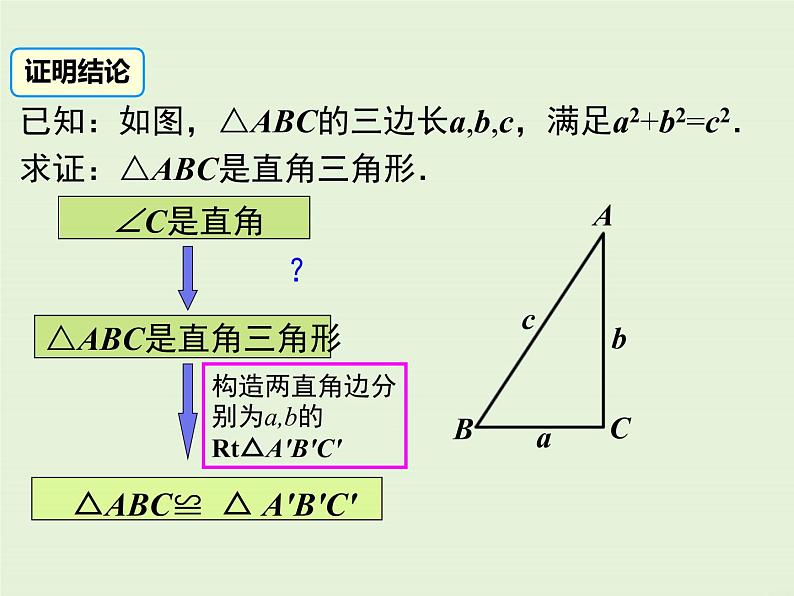
已知：如图，△ABC的三边长a,b,c，满足a2+b2=c2． 求证：△ABC是直角三角形．
构造两直角边分别为a,b的Rt△A′B′C′
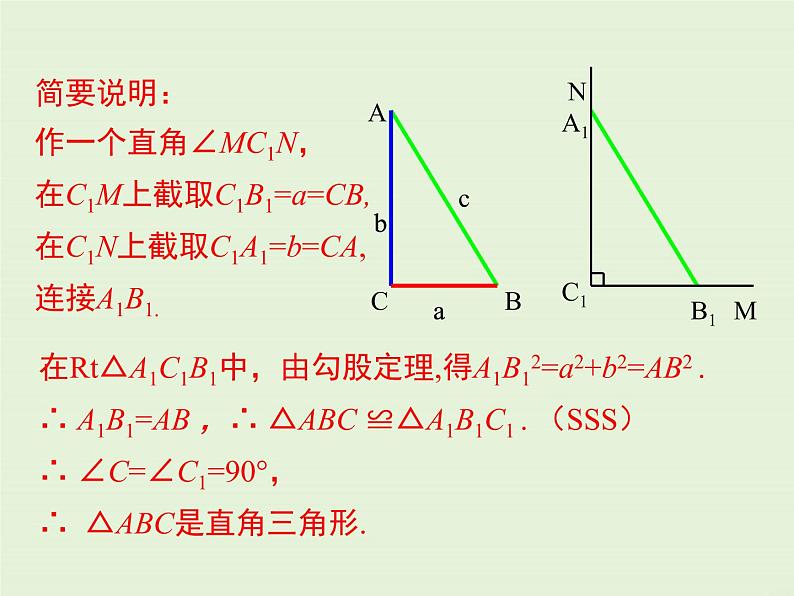
简要说明：作一个直角∠MC1N，在C1M上截取C1B1=a=CB,在C1N上截取C1A1=b=CA,连接A1B1.
在Rt△A1C1B1中，由勾股定理,得A1B12=a2+b2=AB2 .∴ A1B1=AB ，∴ △ABC ≌△A1B1C1 . （SSS）∴ ∠C=∠C1=90°，∴ △ABC是直角三角形.
如果三角形的三边长a 、b 、c满足a2+b2=c2那么这个三角形是直角三角形.
勾股定理的逆定理是直角三角形的判定定理，即已知三角形的三边长，且满足两条较小边的平方和等于最长边的平方，即可判断此三角形为直角三角 ，最长边所对角为直角.
例1：一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图2所示,这个零件符合要求吗?
在△BCD中， 所以△BCD 是直角三角形，∠DBC是直角.因此，这个零件符合要求.
解：在△ABD中， 所以△ABD 是直角三角形，∠A是直角.
例2 下面以a,b,c为边长的三角形是不是直角三角形？如果是,那么哪一个角是直角？
(1) a=15 ， b=8 ，c=17;
解：因为152+82=289，172=289，所以152+82=172，根据勾股定理的逆定理，这个三角形是直角三角形，且∠C是直角.
(2) a=13 ， b=14 ， c=15;
解：因为132+142=365，152=225，所以132+142≠152，不符合勾股定理的逆定理，所以这个三角形不是直角三角形.
(3) a:b: c=3:4:5;
解：设a=3k,b=4k,c=5k,因为(3k)2+(4k)2=25k2,(5k)2=25k2,所以(3k)2+(4k)2=(5k)2,根据勾股定理的逆定理，这个三角形是直角三角形，∠C是直角.
变式1： 已知△ABC，AB=n²-1，BC=2n，AC=n²+1(n为大于1的正整数).试问△ABC是直角三角形吗？若是，哪一条边所对的角是直角？请说明理由
解：∵AB²+BC²=(n²-1)²+(2n)² =n4 -2n²+1+4n² =n4 +2n²+1 =(n²+1)² =AC²，∴△ABC直角三角形，边AC所对的角是直角.
先确定AB、BC、AC、的大小
变式2： 若三角形ABC的三边 a,b,c 满足a2+b2+c2+50=6a+8b+10c. 试判断△ABC的形状.
解：∵ a2+b2+c2+50=6a+8b+10c ∴ a2－6a+9+b2－8b+16+c2－10c+25=0. 即 (a－3)²+ (b－4)²+ (c－5)²=0. ∴ a=3, b=4, c=5 即 a2+b2+c2. ∴△ABC直角三角形.
例3 在正方形ABCD中，F是CD的中点，E为BC上一点，且CE＝ CB，试判断AF与EF的位置关系，并说明理由．
解：AF⊥EF.设正方形的边长为4a, 则EC＝a，BE＝3a，CF＝DF＝2a.在Rt△ABE中，得AE2＝AB2＋BE2＝16a2＋9a2＝25a2.在Rt△CEF中，得EF2＝CE2＋CF2＝a2＋4a2＝5a2.在Rt△ADF中，得AF2＝AD2＋DF2＝16a2＋4a2＝20a2.在△AEF中，AE2＝EF2＋AF2，∴△AEF为直角三角形，且AE为斜边．∴∠AFE＝90°，即AF⊥EF.
如果三角形的三边长a，b，c满足a2+b2=c 那么这个三角形是直角三角形.满足a2+b2=c2的三个正整数，称为勾股数.
3，4，5；5，12，13；6，8，10；7，24，25；8，15，17；9，40，41；10，24，26等等.
一组勾股数，都扩大相同倍数k，得到一组新数，这组数同样是勾股数.
例4：下列各组数是勾股数的是( ) A.6，8，10 B.7，8，9 C.0.3，0.4，0.5 D.52，122，132
方法点拨：根据勾股数的定义，勾股数必须为正整数，先排除小数，再计算最长边的平方是否等于其他两边的平方和即可.
1.如果线段a,b,c能组成直角三角形,则它们的比可以是 ( ) A.3:4:7 B.5:12:13 C.1:2:4 D.1:3:5
将直角三角形的三边长扩大同样的倍数,则得到的三角形 ( )A.是直角三角形 B.可能是锐角三角形C.可能是钝角三角形 D.不可能是直角三角形
4.如果三条线段a，b，c满足a2=c2-b2,这三条线段组成的三角形是直角三角形吗?为什么?
解：是直角三角形.因为a2+b2=c2满足勾股定理的逆定理.
3.以△ABC的三条边为边长向外作正方形, 依次得到的面积是25, 144 , 169, 则这个三角形是______三角形.
5.如图，在正方形ABCD中，AB=4，AE=2，DF=1， 图中有几个直角三角形，你是如何判断的？ 与你的同伴交流.
解:△ABE，△DEF，△FCB均为直角三角形. 由勾股定理知 BE2=22+42=20， EF2=22+12=5， BF2=32+42=25, ∴BE2+EF2=BF2,∴ △BEF是直角三角形.
6.如图，四边形ABCD中，AB⊥AD，已知AD=3cm，AB=4cm，CD=12cm，BC=13cm，求四边形ABCD 的面积.
解：连接BD.在Rt△ABD中,由勾股定理, 得 BD2=AB2+AD2，∴BD=5m，又∵ CD=12cm，BC=13cm∴ BC2=CD2+BD2，∴△BDC是直角三角形.S四边形ABCD=SRt△BCD－SRt△ABD= BD•CD－ AB•AD = (5×12－3×4)=24 m2．
变式：如图，在四边形ABCD中，AC⊥DC，△ADC的面积为30 cm2，DC＝12 cm，AB＝3 cm，BC＝4 cm，求△ABC的面积.
解: ∵ S△ACD=30 cm2，DC＝12 cm.∴ AC=5 cm,又∵∴△ABC是直角三角形, ∠B是直角.∴