人教版九年级上册22.1.3 二次函数y＝a（x－h）2＋k的图象和性质教课课件ppt

这是一份人教版九年级上册22.1.3 二次函数y＝a（x－h）2＋k的图象和性质教课课件ppt，共22页。PPT课件主要包含了yx2，解析列表，yx2+1，yx2-1，描点连线，y-3x2+6，y-3x2-7，－45，1开口方向，2对称轴等内容，欢迎下载使用。

1.会画y=ax2+k，y=a(x-h)2的图象；2.了解y=ax2+k，y=a(x-h)2的图象与y=ax2的关系，能结合图象理解二次函数的性质.
二次函数y=ax2的图象是什么形状呢？什么确定y=ax2的性质？通常怎样画一个函数的图象？
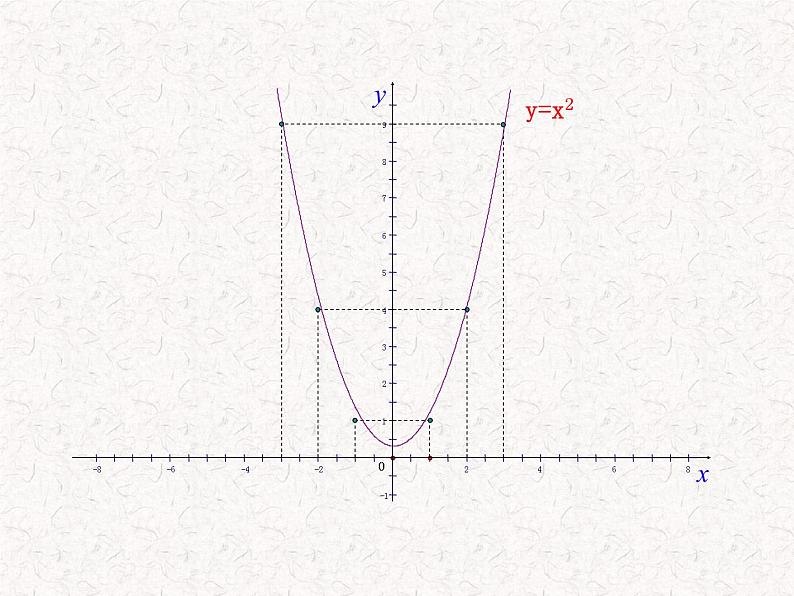
我们来画最简单的二次函数y=x2的图象.
还记得如何用描点法画一个函数的图象吗？
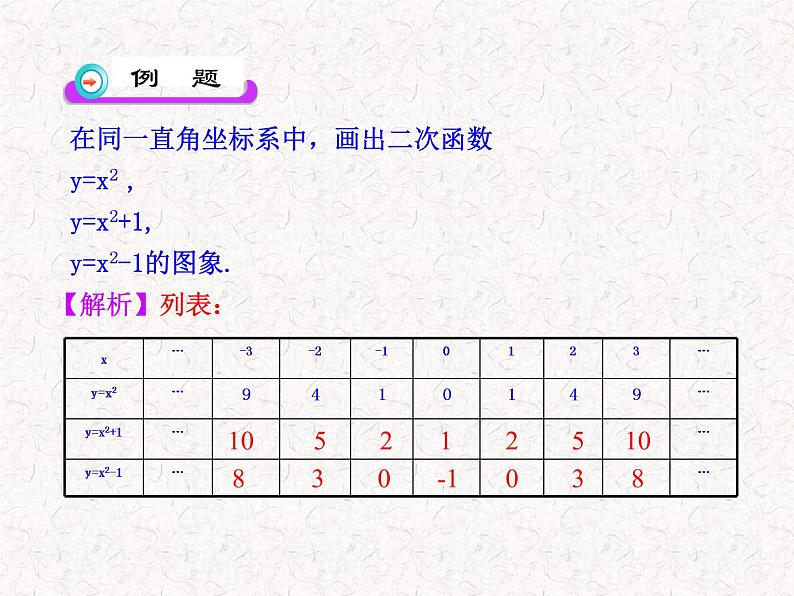
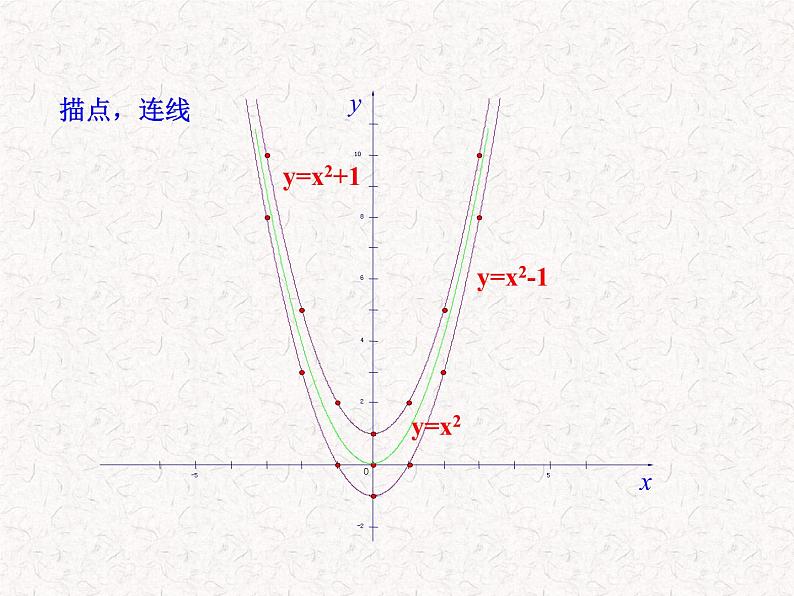
在同一直角坐标系中，画出二次函数y=x2 ,y=x2+1,y=x2-1的图象.
10 5 2 1 2 5 10
8 3 0 -1 0 3 8
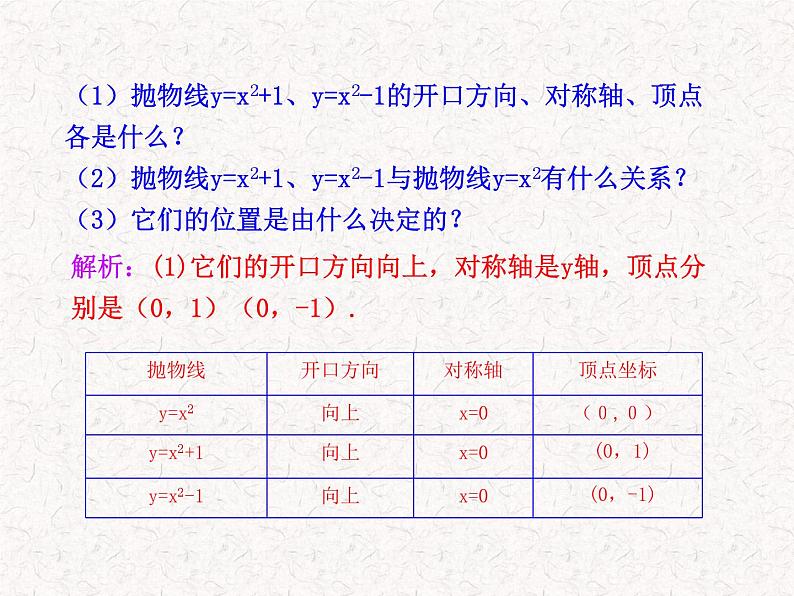
（1）抛物线y=x2+1、y=x2-1的开口方向、对称轴、顶点 各是什么？（2）抛物线y=x2+1、y=x2-1与抛物线y=x2有什么关系？（3）它们的位置是由什么决定的？
解析：(1)它们的开口方向向上，对称轴是y轴，顶点分别是（0，1）（0，-1）.
(2)把抛物线y=x2向上平移1个单位，就得到抛物线y=x2+1；把抛物线y=x2向下平移1个单位，就得到抛物线y=x2-1.(3)它们的位置是由+1、-1决定的.
把抛物线y=2x2向上平移5个单位，会得到哪条抛物线？向下平移3.4个单位呢？
y=2x2+5 y=2x2-3.4
解析：二次项系数小于零时抛物线的开口向下；二次项系数的绝对值越大开口越小，反之越大.
当二次项系数小于零时和二次项系数的绝对值变化时，抛物线将发生怎样的变化？
一般地抛物线y=ax2+k有如下性质：
1.当a>0时，开口向上；当a<0时，开口向下，
2.对称轴是x=0（或y轴），
3.顶点坐标是（0，k），
4.|a|越大开口越小，反之开口越大.
1.把抛物线向上平移6个单位，会得到哪条抛物线？向下平移7个单位呢？
2.在同一直角坐标系中，画出下列二次函数的图象:观察三条抛物线的相互关系，并分别指出它们的开口方向、对称轴及顶点.你能说出抛物线 的开口方向、对称轴及顶点吗？它与抛物线 有什么关系？
画出二次函数 的图象，并考虑它们的开口方向、对称轴和顶点．
可以看出，抛物线 的开口向下，对称轴是经过点（－1，0）且与x轴垂直的直线，我们把它记作x=－1，顶点是（－1，0）；抛物线 的开口向_________，对称轴是________________，顶点是_________________．
抛物线 与抛物线 有什么关系？
可以发现，把抛物线 向左平移1个单位，就得到抛物线 ；把抛物线 向右平移1个单位，就得到抛物线 ．
二次函数y = a﹙x-h﹚2的性质:
当a＞0时，开口向上;当a＜0时，开口向下；
顶点坐标是（h，0）.
1.说出下列二次 函数的开口方向、对称轴及顶点坐标 (1) y=5x2 (2) y=-3x2 +2 (3) y=8x2+6 (4) y= -x2-4
向上，y轴,（0, 0)
向下，y轴,（0, 2)
向上，y轴,（0, 6)
向下，y轴,（0, - 4)
2.说出下列二次函数的开口方向、对称轴及顶点坐标 (1) y=2(x+3)2 (2) y=-3(x-1)2 (3) y=5(x+2)2(4) y=-(x-6)2(5) y=7(x-8)2
向上, x=-3,(-3,0)
向下, x=1,(1,0)
向上, x=-2,(-2,0)
向下, x=6,(6,0)
向上, x=8,(8,0)
3.抛物线y=-3(x+2)2开口向 ，对称轴为 ，顶点坐标为________.4.抛物线y=3x2+0.5 可以看成由抛物线 向 平移 个单位得到的.5.写出一个开口向上，对称轴为x=-2，并且与y轴交于点（0，8）的抛物线解析式____________.
1.（乐山中考）将抛物线y=-x2向左平移2个单位后，得到的抛物线的解析式是（ ）.(A) (B) (C) (D)
【解析】选A.抛物线可以经过适当的平移得到，其平移规律是:“h左加右减, k上加下减”.即自变量加减左右移，函数加减上下移.
2.（哈尔滨中考）在抛物线y＝x2-4上的一个点是（ ）A．（4，4） B．（1，一4）C．（2，0） D．（0，4）
3 .对于任何实数h，抛物线y=(x-h)2与抛物线y=x2的开口 相同.4.将抛物线y= -2x2向左平移一个单位，再向右平移3个单位得抛物线解析式为______________.5.抛物线y=3x2-8 最小值为______.6.抛物线y= -3(x+2)2与x轴，y轴的交点坐标分别为____________________.
(2, 0) (0,12)