初中数学北师大版九年级上册4 探索三角形相似的条件优质导学案

这是一份初中数学北师大版九年级上册4 探索三角形相似的条件优质导学案，共4页。学案主要包含了温故知新，设问导读，自学检测等内容，欢迎下载使用。

自主学习、课前诊断


一、温故知新：


1、相似多边形的定义：____________


2、全等三角形的判定方法：__________________________________


二、设问导读：


阅读课本P89-90完成完成下列问题：


1、根据相似多边形的定义，相似三角形的定义为：_______________________。


如在与中，如果，且


____________________=k． 我们就说与△A′B′C相似，记作_________，k就是它们的相似比．


2.如果两个相似三角形的相似比，这两个三角形_______.


3、想一想、做一做的探索中，两个三角形只有一个角相等________判定两个三角形相似，两角分别相等的两个三角形_____________。


符号语言：











4、例1：证明∆ADE∼∆ABC，运用的方法是:______________，相似三角形的对应边__________从而求出BC。


三、自学检测：


1.判断下列各组中的两个三角形是否相似，并简单说明理由.


(1)在ΔABC中，∠B是直角，∠A=30°；


在ΔA´B´C´中，∠B´是直角，∠C´=60°.


(2)ΔABC与ΔA´B´C´中，∠B=∠B´=75°，∠C=50°，∠A´=55°.

















2、如图，已知：∠B=∠ADE.试说明ΔADE∽ΔABC.
































互动学习、问题解决


一、导入新课


二、交流展示


学用结合、提高能力


1题图


一、巩固训练：


1..如图，DE∥AC,AD=0.7,AB=2.1,DE=3,则AC= .


2、在Rt△ABC可，CD为斜边AB上的高，则下列等式不成立的是（ ）


A.AC2=AD·AB


B.BC2= BD·AB


C.CD2=AD·BD D.AB2=AC·BC





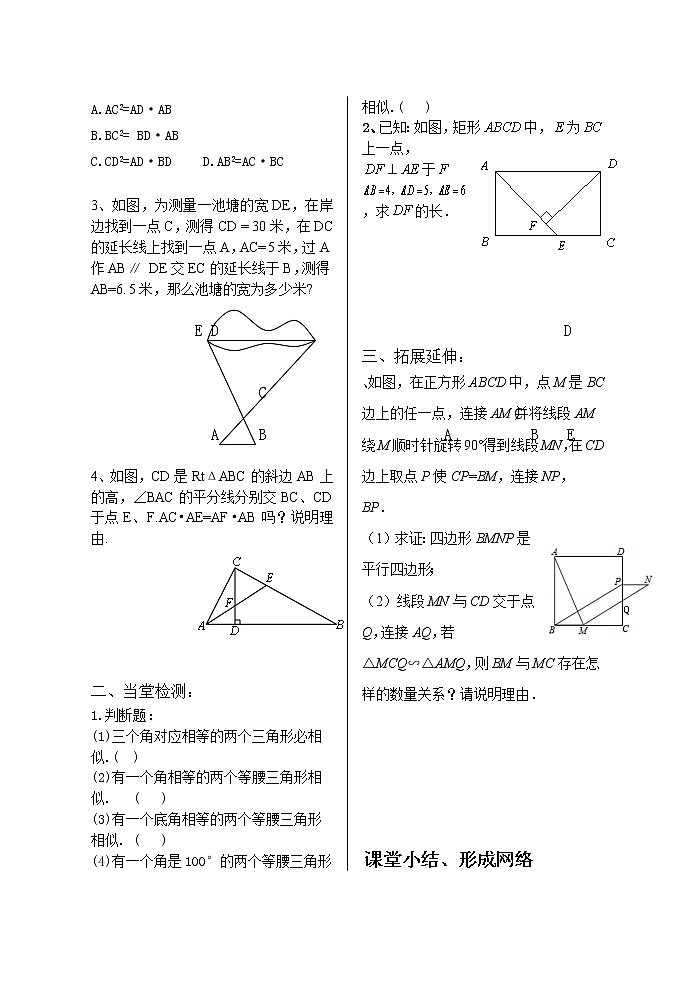
3、如图，为测量一池塘的宽DE，在岸边找到一点C，测得CD = 30米，在DC的延长线上找到一点A，AC=5米，过A作AB ∥ DE交EC的延长线于B，测得AB=6.5米，那么池塘的宽为多少米?





E D D








C


C


A BA BE D





4、如图，CD是RtΔABC的斜边AB上的高，∠BAC的平分线分别交BC、CD于点E、F.AC•AE=AF•AB吗？说明理由.




















二、当堂检测：


1.判断题：


(1)三个角对应相等的两个三角形必相似.( )


(2)有一个角相等的两个等腰三角形相似. ( )


(3)有一个底角相等的两个等腰三角形相似. ( )


(4)有一个角是100°的两个等腰三角形相似.( )


2、已知：如图，矩形中，为上一点，于，求的长．




















三、拓展延伸：


、如图，在正方形ABCD中，点M是BC边上的任一点，连接AM并将线段AM绕M顺时针旋转90°得到线段MN，在CD边上取点P使CP=BM，连接NP，BP．


（1）求证：四边形BMNP是平行四边形；


Q


（2）线段MN与CD交于点Q，连接AQ，若△MCQ∽△AMQ，则BM与MC存在怎样的数量关系？请说明理由．























课堂小结、形成网络


________________________________________________________________________________________________________________________________________








4.4探索三角形相似的条件（1）


三、自我检测


1.（1）∠A=∠A´=30°,∠B=∠B´=90°∴ΔABC∽ΔA´B´C´


（2）∠A=∠A´=55°,∠B=∠B´=75°∴ΔABC∽ΔA´B´C´


2、∵∠B=∠ADE, ∠A=∠A ∴ΔADE∽ΔABC.


一、巩固训练


1. 4.5 2、D


3、∵AB ∥ DE ∴∠B=∠ADE, ∠A=∠A ∴△EDC∽△BAC．∴CD:AC=DE:AB


即:30:5=DE:6.5 ∴DE=39 ∴池塘的宽为39米。





4、∵∠ACB=90°∴∠ACD+∠DCB=90°∵CD⊥AB ∴∠DCB+∠B=90°∴∠ACD=∠B


∵AE平分∠BAC ∴∠CAF=∠EAB 又∵∠ACD=∠B ∴△ABE∽△ACF．


∴AC:AB=AF:AE ∴AC•AE=AF•AB





二、当堂检测：


1. (1)√(2)╳ (3)√ (4)√


2、


三、拓展延伸:


（1）证明：在正方形ABCD中，AB=BC，∠ABC=∠B，


在△ABM和△BCP中，


，


∴△ABM≌△BCP（SAS），


∴AM=BP，∠BAM=∠CBP，


∵∠BAM+∠AMB=90°，


∴∠CBP+∠AMB=90°，


∴AM⊥BP，


∵AM并将线段AM绕M顺时针旋转90°得到线段MN，


∴AM⊥MN，且AM=MN，


∴MN∥BP，


∴四边形BMNP是平行四边形；


（2）解：BM=MC．


理由如下：∵∠BAM+∠AMB=90°，∠AMB+∠CMQ=90°，


∴∠BAM=∠CMQ，


又∵∠B=∠C=90°，


∴△ABM∽△MCQ，


∴=，


∵△MCQ∽△AMQ，


∴△AMQ∽△ABM，


∴=，


∴=，


∴BM=MC．