初中数学浙教版八年级上册第1章 三角形的初步知识综合与测试导学案

这是一份初中数学浙教版八年级上册第1章 三角形的初步知识综合与测试导学案，共11页。学案主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题(每小题3分，共30分)











(第1题)





1．如图，已知MB＝ND，∠MBA＝∠NDC，则下列条件中不能判定△ABM≌△CDN的是(B)


A． ∠M＝∠N


B． AM＝CN


C． AB＝CD


D． AM∥CN


2．若一个三角形的两边长分别是2和4，则该三角形的周长可能是(C)


A． 6 B． 7


C． 11 D． 12


3．如图，在△ABC中，∠BAC＝x，∠B＝2x，∠C＝3x，则∠BAD的度数为(B)


A． 145° B． 150°


C． 155° D． 160°


(第3题)


(第4题)








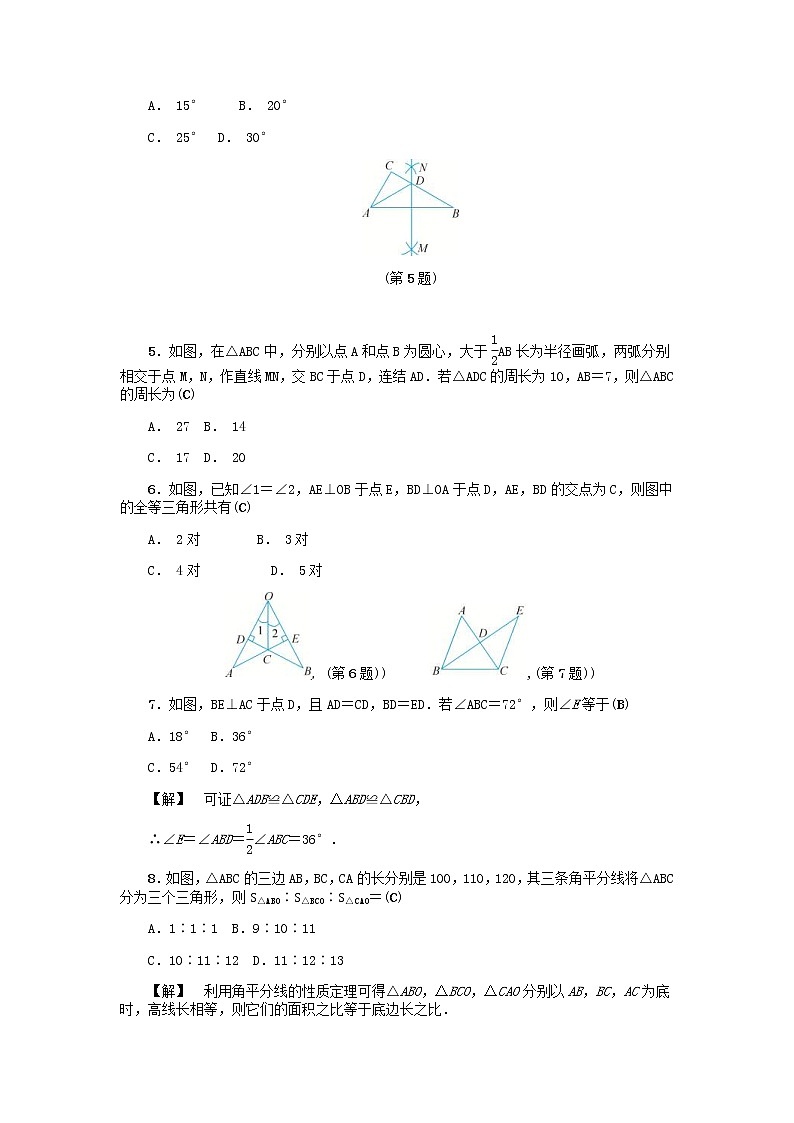
4．如图，把一块含有45°角的直角三角尺的两个顶点放在直尺的对边上．如果∠1＝20°，那么∠2的度数为(C)


A． 15° B． 20°


C． 25° D． 30°





(第5题)





5．如图，在△ABC中，分别以点A和点B为圆心，大于eq \f(1,2)AB长为半径画弧，两弧分别相交于点M，N，作直线MN，交BC于点D，连结AD．若△ADC的周长为10，AB＝7，则△ABC的周长为(C)


A． 27 B． 14


C． 17 D． 20


6．如图，已知∠1＝∠2，AE⊥OB于点E，BD⊥OA于点D，AE，BD的交点为C，则图中的全等三角形共有(C)


A． 2对 B． 3对


C． 4对 D． 5对


, (第6题)) ,(第7题))


7．如图，BE⊥AC于点D，且AD＝CD，BD＝ED．若∠ABC＝72°，则∠E等于(B)


A．18° B．36°


C．54° D．72°


【解】 可证△ADB≌△CDE，△ABD≌△CBD，


∴∠E＝∠ABD＝eq \f(1,2)∠ABC＝36°．


8．如图，△ABC的三边AB，BC，CA的长分别是100，110，120，其三条角平分线将△ABC分为三个三角形，则S△ABO∶S△BCO∶S△CAO＝(C)


A．1∶1∶1 B．9∶10∶11


C．10∶11∶12 D．11∶12∶13


【解】 利用角平分线的性质定理可得△ABO，△BCO，△CAO分别以AB，BC，AC为底时，高线长相等，则它们的面积之比等于底边长之比．


,(第8题)) ,(第9题))


9．如图，AB∥CD, AP，CP分别平分∠BAC和∠ACD，PE⊥AC于点E，且PE＝3 cm，则AB与CD之间的距离为(B)


A． 3 cm B． 6 cm


C． 9 cm D． 无法确定


【解】 过点P作PF⊥AB，垂足为F，延长FP交CD于点G．


∵AB∥CD，∴∠FGD＝∠AFG＝90°，


∴PG⊥CD．


∵AP平分∠BAC，PF⊥AB，PE⊥AC，


∴PF＝PE＝3．


同理，PG＝PE＝3，


∴FG＝PF＋PG＝3＋3＝6，


即AB与CD之间的距离为6 cm．


10．如图，AD是△ABC的一个外角的角平分线，P是AD上异于点A的任意一点，设PB＝m，PC＝n，AB＝c，AC＝b，则m＋n与b＋c的大小关系是(A)


A． m＋n＞b＋c B． m＋n＜b＋c


C． m＋n＝b＋c D． 无法确定


导学号：91354007


,(第10题)) ,(第10题解))


【解】 如解图，在BA的延长线上取一点E，使AE＝AC，连结ED，EP．


∵AD是△ABC的一个外角的角平分线，


∴∠CAD＝∠EAD．


在△ACP和△AEP中，∵eq \b\lc\{(\a\vs4\al\c1(AC＝AE，,∠CAP＝∠EAP，,AP＝AP，))


∴△ACP≌△AEP(SAS)．∴PC＝PE．


在△PBE中，PB＋PE＞AB＋AE，


即PB＋PC>AB＋AC．


∵PB＝m，PC＝n，AB＝c，AC＝b，


∴m＋n＞b＋c．


二、填空题(每小题3分，共30分)


11．有下列命题：①对顶角相等；②同旁内角互补；③全等三角形的对应角相等；④两直线平行，同位角相等．其中是假命题的是__②__(填序号)．





(第12题)





12．如图，AC与BD相交于点O，∠A＝∠D，请添加一个适当的条件：AO＝DO(答案不唯一)，使得△AOB≌△DOC．


13．已知三角形的三边长分别为3，5，x，则化简式子|x－2|＋|x－9|＝__7__．


【解】 提示：2＜x＜8．





(第14题)





14．如图，在△ABC中，已知∠1＝∠2，BE＝CD，AB＝5，AE＝2，则CE＝__3__．


【解】 在△ABE和△ACD中，


∵∠1＝∠2，∠A＝∠A，BE＝CD，


∴△ABE≌△ACD(AAS)，∴AC＝AB＝5．


∵AE＝2，∴CE＝3．


15．如图，在4×5的网格中，每个小正方形的边长都为1，在图中找两个格点D和E，使∠ABE＝∠ACD＝90°，并使AC＝DC，AB＝EB，则四边形BCDE的面积为__3__．


,(第15题)) ,(第15题解))


【解】 如解图，四边形BCDE的面积为8－3－eq \f(3,2)－eq \f(1,2)＝3．





(第16题)





16．如图，四边形ABCD的对角线AC，BD相交于点O，△ABO≌△ADO．有下列结论：①AC⊥BD；②CB＝CD；③△ABC≌△ADC；④AD＝CD．其中正确结论的序号是①②③．


【解】 ∵△ABO≌△ADO，


∴∠AOB＝∠AOD，AB＝AD，∠BAO＝∠DAO．


∵∠AOB＋∠AOD＝180°，


∴∠AOB＝∠AOD＝90°，


∴AC⊥BD，故①正确．


在△ABC和△ADC中，∵eq \b\lc\{(\a\vs4\al\c1(AB＝AD，,∠BAC＝∠DAC，,AC＝AC，))


∴△ABC≌△ADC(SAS)，


∴CB＝CD，故②③正确．


AD与CD不一定相等，故④错误．


综上所述，正确结论的序号是①②③．





(第17题)


17．如图，△ABC三边上的中线AD，BE，CF的交点为G．若S△ABC＝12，则图中阴影部分的面积是__4__．


【解】 ∵△ABC的三条中线AD，BE，CF交于点G，∴S△ABD＝S△ACD，S△AFG＝S△BFG，S△AGE＝S△CGE，S△BDG＝S△CDG，


∴S△ABG＝S△ACG，∴S△BFG＝S△CGE．


同理，S△BFG＝S△BDG，∴图中6个小三角形的面积都相等．∴S阴影＝eq \f(1,3)S△ABC＝4．


18．如图，在△ABC中，AB＝5，AC＝3，AD是△ABC的中线，则AD长的取值范围是1




(第18题)





【解】 延长AD至点E，使ED＝AD，连结BE．


∵AD是△ABC的中线，


∴BD＝CD．


在△EBD和△ACD中，


∵eq \b\lc\{(\a\vs4\al\c1(BD＝CD，,∠BDE＝∠CDA，,ED＝AD，))


∴△EBD≌△ACD(SAS)，∴EB＝AC＝3．


∵AB＝EB

∴5－3<2AD<5＋3，∴1




(第19题)


19．如图，在△ABC中，∠A＝52°，∠ABC与∠ACB的平分线交于点D1，∠ABD1与∠ACD1的平分线交于点D2……依次类推，∠BD5C的度数为__56°__．


【解】 ∵∠A＝52°，


∴∠ABC＋∠ACB＝128°．


∵BD1，CD1分别平分∠ABC和∠ACB，


∴∠D1BC＋∠D1CB＝eq \f(1,2)(∠ABC＋∠ACB)＝64°，∴∠D1＝180°－64°＝116°．


同理，∠D2＝180°－64°－eq \f(1,2)×64°＝84°……


∴∠D5＝180°－64°－eq \f(1,2)×64°－eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))eq \s\up12(2)×64°－eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))eq \s\up12(3)×64°－eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))eq \s\up12(4)×64°＝56°．


20．如图，图①是一块边长为1，周长记为P1的等边三角形纸板，沿图①的底边剪去一块边长为eq \f(1,2)的等边三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的等边三角形纸板(即边长为前一块被剪掉等边三角形纸板边长的eq \f(1,2))后得到图③……记第n(n≥3)块纸板的周长为Pn，则Pn－Pn－1＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))eq \s\up12(n－1)．





(第20题)


【解】 ∵P1＝3，P2＝2eq \f(1,2)，P3＝2eq \f(3,4)，P4＝2eq \f(7,8)，


∴P3－P2＝eq \f(1,4)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))eq \s\up12(2)，P4－P3＝eq \f(1,8)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))eq \s\up12(3)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))eq \s\up12(4－1)……依次类推得Pn－Pn－1＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))eq \s\up12(n－1)．


三、解答题(共40分)


21．(5分)如图，已知∠AOB内有两点M，N，请找出一点P，使得PM＝PN，且点P到OA和OB的距离相等(要求：尺规作图，保留作图痕迹)．


(第21题)


(第21题解)








【解】 作法如下：


(1)连结MN，作MN的垂直平分线l．


(2)作∠AOB的平分线OC，与l相交于点P，则点P即为所求，如解图所示．





(第22题)


22．(5分)如图，∠BAC＝∠DAM，AB＝AN，AD＝AM．求证：∠B＝∠ANM．


【解】 ∵∠BAC＝∠DAM，


∴∠BAC－∠DAC＝∠DAM－∠DAC，即∠BAD＝∠NAM．


在△ABD和△ANM中，∵eq \b\lc\{(\a\vs4\al\c1(AB＝AN，,∠BAD＝∠NAM，,AD＝AM，))


∴△ABD≌△ANM(SAS)，∴∠B＝∠ANM．





(第23题)


23．(6分)如图，在△ABC中，AB＝CB，∠ABC＝90°，D为AB的延长线上一点，点E在BC边上，且BE＝BD，连结AE，DE，CD．


(1)求证：△ABE≌△CBD．


(2)若∠CAE＝27°，∠ACB＝45°，求∠BDC的度数．


【解】 (1)∵∠ABC＝90°，


∴∠CBD＝90°＝∠ABC．


在△ABE和△CBD中，∵eq \b\lc\{(\a\vs4\al\c1(AB＝CB，,∠ABE＝∠CBD，,BE＝BD，))


∴△ABE≌△CBD(SAS)．


(2)∵△ABE≌△CBD，∴∠AEB＝∠CDB．


∵∠AEB为△AEC的一个外角，


∴∠AEB＝∠CAE＋∠ACB＝27°＋45°＝72°，


∴∠BDC＝72°．


24．(6分)如图，已知BD，CE是△ABC的高线，点F在BD上，BF＝AC，点G在CE的延长线上，CG＝AB，连结AF，AG．求证：AG⊥AF．





(第24题)





【解】 设BD与CG相交于点H．


∵BD，CE是△ABC的高线，∴∠BEC＝∠CDB＝90°．


∵∠EHB＝∠DHC，∴∠EBH＝∠DCH．


又∵BF＝CA，AB＝GC，∴△ABF≌△GCA(SAS)，∴∠BAF＝∠G．


∵∠AEG＝90°，∴∠G＋∠GAE＝90°，


∴∠BAF＋∠GAE＝90°，即∠GAF＝90°，


∴AG⊥AF．





(第25题)


25．(8分)如图，已知BE，CF分别是△ABC中AC，AB边上的高线，在BE的延长线上取点P，使PB＝AC，在CF的延长线上取点Q，使CQ＝AB．求证：AQ⊥AP．


【解】 ∵BE，CF分别是△ABC中AC，AB边上的高线，


∴∠AEB＝∠AFC＝90°，


∴∠ABP＋∠EAF＝90°，∠ACQ＋∠EAF＝90°，∴∠ABP＝∠ACQ．


在△ABP和△QCA中，∵PB＝AC，∠ABP＝∠QCA，AB＝QC，


∴△ABP≌△QCA(SAS)，∴∠APB＝∠QAC，


∴∠APB＋∠PAE＝∠QAC＋∠PAE，


即180°－∠AEP＝∠PAQ，


∴∠PAQ＝90°，即AQ⊥AP．


26．(10分)旧知新意：我们知道，三角形的一个外角等于与它不相邻的两个内角的和，那么三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢？


(1)尝试探究：


如图①，∠DBC与∠ECB分别为△ABC的两个外角，试探究∠A与∠DBC＋∠ECB之间的数量关系．


(2)初步运用：


如图②，在△ABC纸片中剪去△CED，得到四边形ABDE．若∠1＝130°，则∠2－∠C＝50°．小明联想到了曾经解决的一个问题：如图③，在△ABC中，BP，CP分别平分外角∠DBC，∠ECB，则∠P与∠A有何数量关系？请利用上面的结论直接写出答案：∠P＝90°－eq \f(1,2)∠A．





(第26题)





(3)拓展提升：


如图④，在四边形ABCD中，BP，CP分别平分外角∠EBC，∠FCB，则∠P与∠A，∠D有何数量关系？导学号：91354008


【解】 (1)∠DBC＋∠ECB＝(180°－∠ABC)＋(180°－∠ACB)＝360°－(∠ABC＋∠ACB)＝360°－(180°－∠A)＝180°＋∠A．


(2)∵∠1＋∠2＝180°＋∠C，


∴130°＋∠2＝180°＋∠C，∴∠2－∠C＝50°．


∵∠DBC＋∠ECB＝180°＋∠A，BP，CP分别平分外角∠DBC，∠ECB，


∴∠PBC＋∠PCB＝eq \f(1,2)(∠DBC＋∠ECB)＝eq \f(1,2)(180°＋∠A)，


∴∠P＝180°－(∠PBC＋∠PCB)＝180°－eq \f(1,2)(180°＋∠A)＝90°－eq \f(1,2)∠A，


即∠P＝90°－eq \f(1,2)∠A．





(第26题解)





(3)如解图，延长BA，CD相交于点Q，则∠P＝90°－eq \f(1,2)∠Q，


∴∠Q＝180°－2∠P，


∴∠BAD＋∠CDA＝180°＋∠Q＝180°＋180°－2∠P＝360°－2∠P．