初中数学北师大版九年级上册2 矩形的性质与判定教学演示课件ppt

这是一份初中数学北师大版九年级上册2 矩形的性质与判定教学演示课件ppt，共24页。PPT课件主要包含了等于斜边的一半，cm2，①②③等内容，欢迎下载使用。

1．有一个角是____的平行四边形叫做矩形．练习1：已知四边形ABCD，若AB∥CD，AD∥BC，且∠D＝90°，则四边形ABCD为____．2．矩形的四个角都是____；矩形的对角线____．
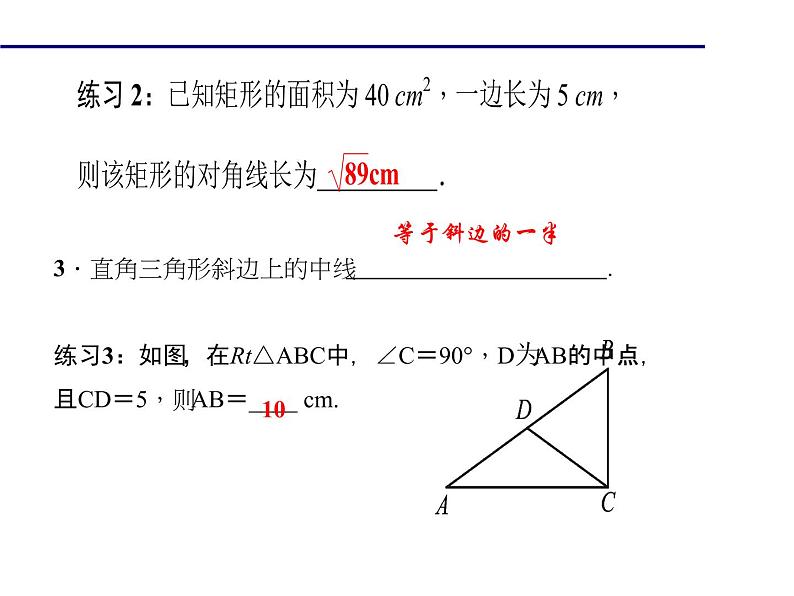
3．直角三角形斜边上的中线 ．练习3：如图，在Rt△ABC中，∠C＝90°，D为AB的中点，且CD＝5，则AB＝____ cm.
1．下列性质中，矩形具有但平行四边形不一定具有的是( )A．对边相等　　　　　　B．对角相等C．对角线相等 D．对边平行2．矩形具有而菱形不具有的性质是( )A．两组对边分别平行 B．对角线相等C．对角线互相平分 D．两组对角分别相等
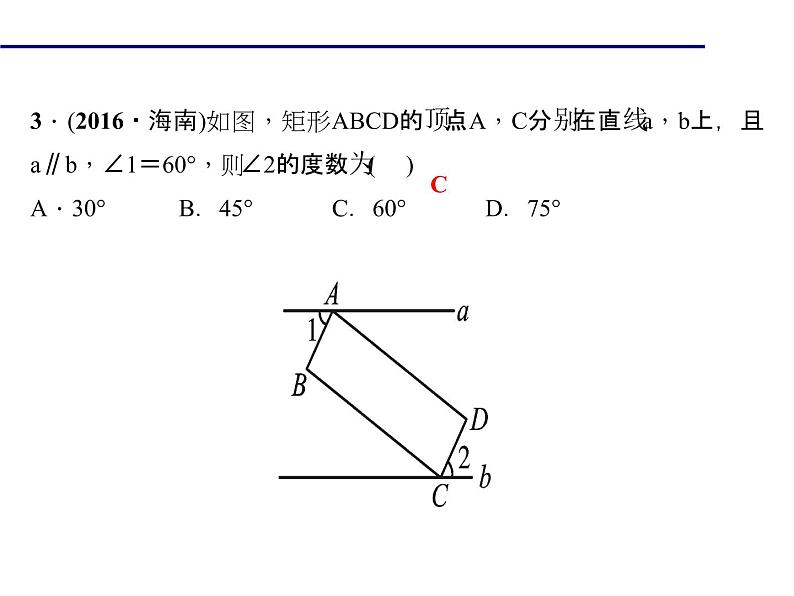
3．(2016·海南)如图，矩形ABCD的顶点A，C分别在直线a，b上，且a∥b，∠1＝60°，则∠2的度数为( )A．30°　　　B．45°　 　　C．60°　 　　D．75°
5．如图，Rt△ABC中，∠C＝90°，AC＝BC＝6，点E是斜边AB上任意一点，作EF⊥AC于点F，EG⊥BC于点G，则矩形CFEG的周长是____．
6．如图，矩形ABCD的对角线相交于点O，CE∥BD，DE∥AC.求证：四边形DOCE是菱形．∵四边形ABCD是矩形，∴DB＝AC，DO＝OB，AO＝OC，∴DO＝OC，∵EC∥BD，DE∥AC，∴四边形DOCE是平行四边形，∴▱DOCE是菱形
7．(2016·南充)如图，对折矩形纸片ABCD，使AB与DC重合得到折痕EF，将纸片展平；再一次折叠，使点D落到EF上点G处，并使折痕经过点A，展平纸片后∠DAG的大小为( )A．30° B．45° C．60° D．75°
8．(易错题)如图，在Rt△ABC中，∠ACB＝90°，点D，E，F分别是AB，BC，CA的中点，若EF＝4 cm，则CD＝____cm.9．如图，“人字形”屋梁中，AB＝AC，点E，F，D分别是AB，AC，BC的中点，若AB＝6 m，∠B＝30°，则支撑“人字形”屋梁的木料DE，AD，DF共有____m.
10．直角三角形斜边上的高与中线分别是5 cm和6 cm，则它的面积是 ．11．如图，点O是矩形ABCD的对角线AC的中点，点M是AD的中点，若AB＝5，AD＝12，则四边形ABOM的周长为____．
12．如图，已知矩形ABCD中，对角线AC，BD相交于点O，AE⊥BD于点E，若∠DAE∶∠BAE＝3∶1，则∠EAC的度数是( )A．18°　　　B．36°　　　C．45°　　　D．72°
15．如图所示，在△ABC中，BD，CE是高，点G，F分别是BC，DE的中点，则下列结论中：①GE＝GD；②GF⊥DE；③GF平分∠DGE；④∠DGE＝60°.其中正确的是 ．(填写序号)
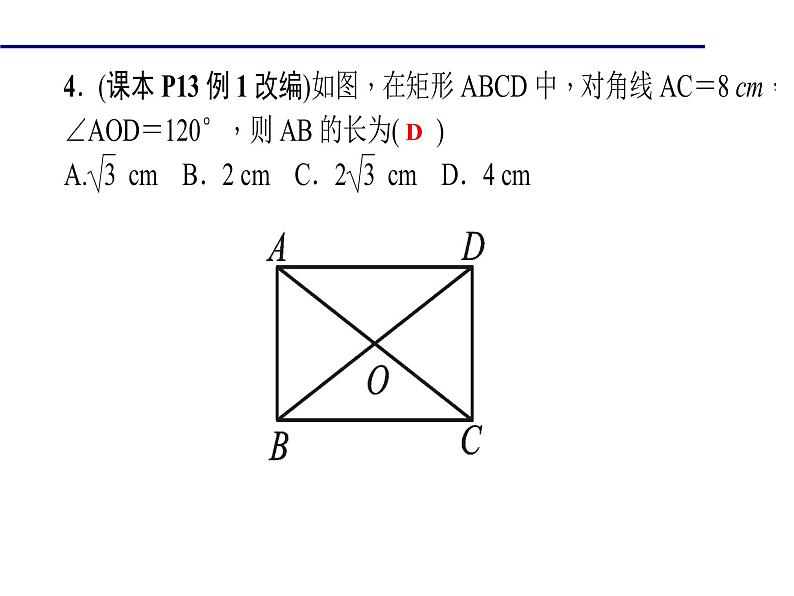
16．(2016·广州)如图，矩形ABCD的对角线AC，BD相交于点O，若AB＝AO，求∠ABD的度数．
17．如图所示，矩形ABCD的对角线AC，BD相交于点O，AE⊥BD，垂足为点E，∠1＝∠2，OB＝6 cm.(1)求∠BOC的度数；(2)求△DOC的周长．(1)∵AE⊥BD, ∴∠AEO＝∠AEB＝90°，又∵AE＝AE，∠1＝∠2，∴△AEO≌△AEB.∴AB＝AO.又∵OA＝OB, ∴△AOB为等边三角形，∴∠AOB＝60°，∴∠BOC＝120°
(2)由矩形的性质可得△OCD≌△OAB，∴OC＝OA＝OB＝6 cm. ∴△DOC的周长为18 cm
18．(阿凡题：1071403)(2017·邵阳模拟)准备一张矩形纸片，按下图操作：将△ABE沿BE翻折，使点A落在对角线BD上的M点，将△CDF沿DF翻折，使点C落在对角线BD上的N点．(1)求证：四边形BFDE是平行四边形；(2)若四边形BFDE是菱形，AB＝2，求菱形BFDE的面积．