





所属成套资源:2024-2025学年北师大(2024)版数学七年级下册 课件
北师大版(2024)七年级下册(2024)第五章 图形的轴对称2 简单的轴对称图形教课内容ppt课件
展开
这是一份北师大版(2024)七年级下册(2024)第五章 图形的轴对称2 简单的轴对称图形教课内容ppt课件,共33页。PPT课件主要包含了学习目标,新课导入,新知探究,提出问题,归纳总结,典型例题,针对练习,判断下列说法的正误,课堂小结,等腰三角形的性质等内容,欢迎下载使用。
1.理解等腰三角形和等边三角形的轴对称性及其相关性质。【重点】2.会应用等腰三角形和等边三角形的性质解决实际问题。【难点】
等腰三角形是生活中常见的图形。
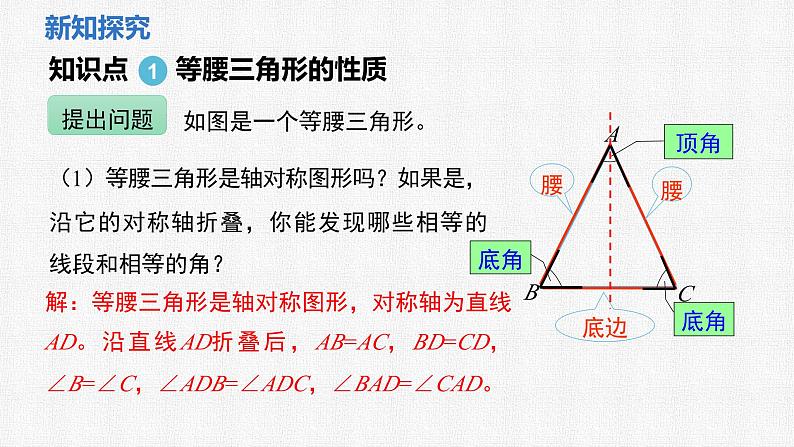
如图是一个等腰三角形。
知识点 等腰三角形的性质
(1)等腰三角形是轴对称图形吗?如果是,沿它的对称轴折叠,你能发现哪些相等的线段和相等的角?
解:等腰三角形是轴对称图形,对称轴为直线AD。沿直线AD折叠后,AB=AC,BD=CD,∠B=∠C,∠ADB=∠ADC,∠BAD=∠CAD。
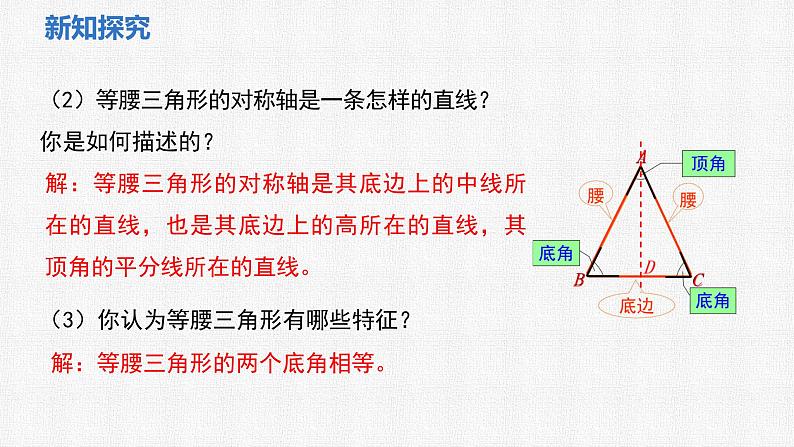
(2)等腰三角形的对称轴是一条怎样的直线? 你是如何描述的?
解:等腰三角形的对称轴是其底边上的中线所在的直线,也是其底边上的高所在的直线,其顶角的平分线所在的直线。
(3)你认为等腰三角形有哪些特征?
解:等腰三角形的两个底角相等。
1.等腰三角形是轴对称图形。2.等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线是等腰三角形的对称轴。3.等腰三角形的两个底角相等。
如图是一个等边三角形。
(2) 你能发现它的哪些特征?
解:等边三角形有 3 条对称轴。
解:①等边三角形三个内角都相等,且均为60°;
②等边三角形是轴对称图形,它有三条对称轴,对称轴是每条边上的中线、高线或角的平分线所在的直线;
③等边三角形每条边上的中线、高线和角平分线互相重合。
(1) 等边三角形有几条对称轴?
例1 等腰三角形的一个内角是 50°,则这个三角形的底角的大小是 ( ) A.65° 或 50° B.80° 或 40° C.65° 或 80° D.50° 或 80°
【解析】当50°的角是底角时,三角形的底角就是50°;当50°的角是顶角时,两底角相等,根据三角形的内角和定理,易得底角是65°。所以三角形的底角可能是50°或65°。故选A。
例2 如图,在△ABC中,AB = AC,点D在AC上,且BD = BC = AD,求∠A和∠C的度数。
解:因为AB=AC,BD=BC=AD,所以∠ABC=∠C=∠BDC,∠A=∠ABD。设∠A=x°,即∠A=∠ABD=x°。因为∠A+∠ABD+∠ADB=180°,∠BDC+∠ADB=180°,所以∠BDC=2x°,所以∠ABC=∠C=∠BDC=2x°,所以x+2x+2x=180,解得x=36,所以∠A=36°,∠C=72°。
(1)等腰直角三角形的每一个锐角的度数是 ;(2)如果等腰三角形的底角等于40°,那么它的顶角的度数是 ;(3)如果等腰三角形有一个内角等于80°,那么这个三角形的最小内角等于 ;(4)△ABC中,AB = AC,∠A = 36°,则∠B = °,∠C = _ _°;(5)△ABC中,AB = AC,∠B = 36°,则∠A = °,∠C = °。
1. 等腰三角形的顶角一定是锐角。2. 等腰三角形的底角可能是锐角或者直角、钝角。3. 钝角三角形不可能是等腰三角形。 4. 等腰三角形的顶角平分线一定垂直于底边。5. 等腰三角形的角平分线、中线和高互相重合。6. 等腰三角形底边上的中线一定平分顶角。
等腰三角形的两个底角相等
等腰三角形顶角的平分线、底边上的中线和底边上的高重合(三线合一)
1.等腰三角形的两边长分别为 4 厘米和 9 厘米,则这个三角形的周长为 ( )A. 22厘米B. 17 厘米C. 13厘米D. 17 厘米或 22 厘米
2.如图,已知AB=AC=BD,那么∠1与∠2之间满足的关系是( )A. ∠1=∠2 B. ∠1+3∠2=180°C. 2∠1+∠2=180°D. 3∠1﹣∠2=180°
3.如图,BD是等边三角形ABC的边AC上的高,以点D为圆心,DB长为半径作弧交BC的延长线于点E,则∠DEC= 。
4.等腰三角形中,一腰上的中线把三角形的周长分为6cm和15cm的两部分,则该三角形的腰长为 。
5.如图,AB=AC,点P在△ABC的内部,满足PB=PC。试说明:AP⊥BC。
解:在△ABP和△ACP中,因为AB=AC,PB=PC,AP=AP,所以△ABP≌△ACP(SSS),所以∠BAP=∠CAP,则根据等腰三角形三线合一定理,得AP⊥BC。
北师大版-数学-七年级下册
第2课时 线段垂直平分线的性质及作法
1.理解线段垂直平分线的性质。【重点】2.能运用线段垂直平分线的性质解决实际问题。【难点】3.会用尺规作线段的垂直平分线,了解作图的道理。
1.什么是轴对称图形?
解:如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫作轴对称图形,这条直线叫作对称轴。
2.轴对称的性质是什么?
解:在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等。
在纸上画一条线段,你能不用任何工具找到这条线段的对称轴吗?
1.线段本身所在的直线是它的一条对称轴。
2.对折,使点A,B重合,折痕OC与AB相交于点C,折痕OC也是它的一条对称轴。
知识点 线段垂直平分线的定义
线段是轴对称图形,垂直并且平分线段的直线是它的一条对称轴。垂直平分线的定义:垂直于一条线段,并且平分这条线段的直线,叫作这条线段的垂直平分线(简称中垂线)。
如图,直线l是线段AB的垂直平分线,点C是l上的任意一点。在线段AB上画出以直线l为对称轴的一组对应点D和D’,连接CD和CD’。
(1)你认为线段CD和CD’之间有什么关系?说说你的理由。
解:CD=CD’。因为点D和点D’关于直线l对称,所以OD=OD’,∠COD=∠COD’=90°。又因为OC=OC,所以△COD≌△COD’(SAS),所以CD=CD’。
知识点 线段垂直平分线的性质
(2)特别地,当点D与点A重合时,点D’位于什么位置?此时,线段CD和CD’之间还有(1)中的关系吗?
解:当点D与点A重合时,点D’与点B重合,此时CD和CD’依然相等,即AC=BC。
垂直平分线的性质:线段垂直平分线上的点到这两条线段两个端点的距离相等。
因为点C在线段AB的垂直平分线上,所以AC=BC。
例1 如图,DE是AC的垂直平分线,AB=12厘米,BC=10厘米,则△BCD的周长为 ( )A.22厘米 B.16厘米C.26厘米 D.25厘米
解析:根据线段垂直平分线的性质,得CD=AD,故△BCD的周长为DC+BD+BC=AD+BD+BC=AB+BC=12+10=22(厘米)。
1.如图,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
2.如图,AB是△ABC的一条边,DE是AB的垂直平分线,垂足为E,并交BC于点D,已知AB=8cm,BD=6cm,那么EA= cm,DA= cm。
A.6 B.5 C.4 D.3
知识点 线段垂直平分线的作法
例2 如图,已知线段AB,请用尺规作线段AB的垂直平分线。
直线CD就是线段AB的垂直平分线。
如图,某地由于居民增多,要在公路l旁增加一个公共汽车站,A,B是路边两个新建小区,这个公共汽车站C建在什么位置,能使两个小区到车站的路程一样长?(要求:尺规作图,保留作图痕迹,不写作法)
解:如图所示,点O即为所求。解析:连接AB,作AB的垂直平分线交直线l于O,交AB于E。因为EO是线段AB的垂直平分线,所以点O到点A,B的距离相等。所以这个公共汽车站C应建在O点处,才能使到两个小区的路程一样长。
线段垂直平分线上的点到这条线段两个端点的距离相等
见垂直平分线,得线段相等
1.如图,在△ABC中,AB=AE,且AD⊥BC,EF垂直平分AC,交 AC于点F,交BC于点E,若△ABC的周长为16,AC=6,则DC为( )
A.5 B.8 C.9 D.10
2.如图,∠BAC=140°,若DM和EN分别垂直平分AB和AC,则∠DAE等于( )
A.100° B.90° C.80° D.70°
3.如图,AB垂直平分CD,AC=6,BD=4,则四边形ADBC的周长是_____。
5.如图,已知AD是△ABC的高线,AD的垂直平分线分别交AB,AC于点E,F。
解:(1)因为EF是AD的垂直平分线,所以EF⊥AD,因为AD是△ABC的高线,所以BC⊥AD,所以EF∥BC,所以∠AEF=∠B=40°。
(1)若∠B=40°,求∠AEF的度数;
相关课件
这是一份初中数学北师大版(2024)七年级下册(2024)2 简单的轴对称图形教学演示ppt课件,共18页。PPT课件主要包含了学习目标,新课导入,你发现了什么图形,新知探究,解CDCD’,几何语言,判一判,课堂小结,角平分线,尺规作图等内容,欢迎下载使用。
这是一份初中数学北师大版(2024)七年级下册1 同底数幂的乘法教学ppt课件,共17页。PPT课件主要包含了学习目标,新课导入,新知探究,乘方的意义,乘法的结合律,探究1,尝试•交流,am·an,·a·a··a,a·a··a等内容,欢迎下载使用。
这是一份初中数学北师大版(2024)七年级下册(2024)2 简单的轴对称图形课文内容ppt课件,共24页。PPT课件主要包含了三线合一,等边对等角,有三条对称轴等内容,欢迎下载使用。









