数学2 简单的轴对称图形教课内容ppt课件

这是一份数学2 简单的轴对称图形教课内容ppt课件，共21页。
1.了解角是轴对称图形。2.理解并掌握角平分线的性质定理。3.能利用尺规作一个角的角平分线。
问题 观察下列常见的物品，你能想到数学中的哪个图形？
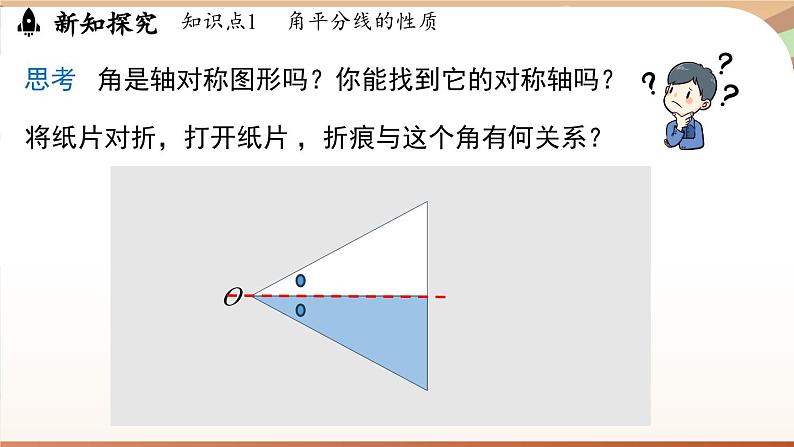
思考 角是轴对称图形吗？你能找到它的对称轴吗？
将纸片对折，打开纸片 ，折痕与这个角有何关系？
知识点1 角平分线的性质
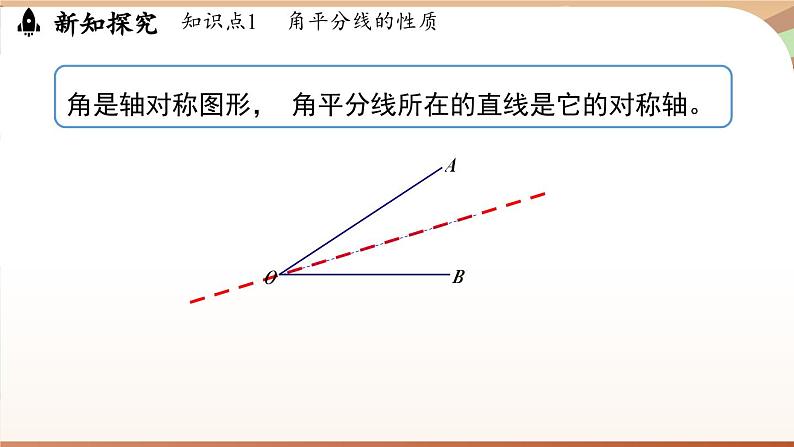
角是轴对称图形， 角平分线所在的直线是它的对称轴。
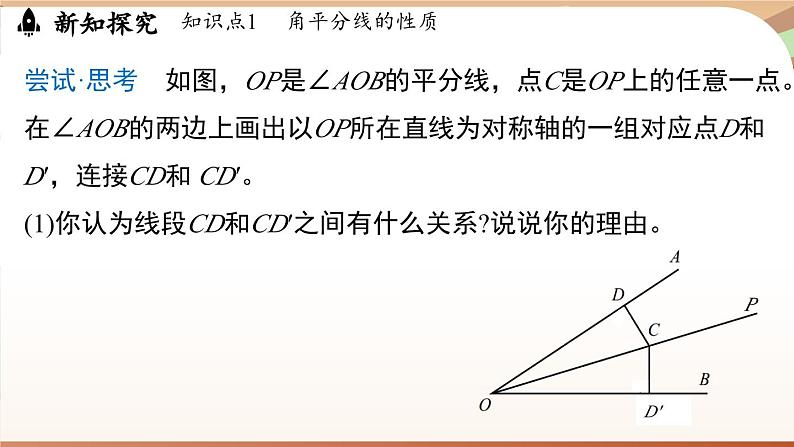
尝试·思考 如图，OP是∠AOB的平分线，点C是OP上的任意一点。在∠AOB的两边上画出以OP所在直线为对称轴的一组对应点D和D′，连接CD和 CD′。(1)你认为线段CD和CD′之间有什么关系?说说你的理由。
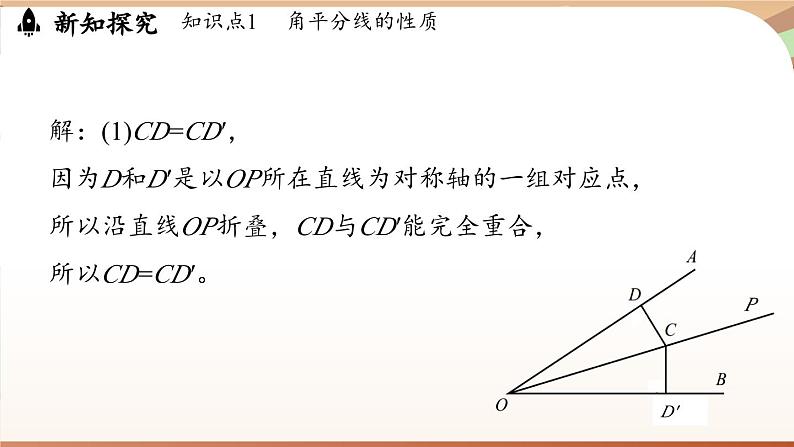
解：(1)CD=CD′，因为D和D′是以OP所在直线为对称轴的一组对应点，所以沿直线OP折叠，CD与CD′能完全重合，所以CD=CD′。
(2)特别地，当CD⊥OA时（如图），CD′与OB有怎样的位置关系?为什么?此时，线段CD和CD′之间还有(1)中的关系吗?
(2)CD′⊥OB，由对称可知∠CDO=∠CD′O=90°。此时线段CD与CD′之间还有(1)中的关系。角平分线上的点到这个角的两边的距离相等。
由此你能得到什么结论?
角平分线的性质定理：角的平分线上的点到这个角的两边的距离相等。
符号语言：因为OC 平分∠AOB，PD⊥OA，PE⊥OB，所以PD = PE。
例1 如图，在△ABC中，∠ACB=90°，AD 平分∠BAC交BC于点D，若BC=10，点D到AB的距离为4，则BD的长为( )A.6 B.8 C.5 D.4
解析:如图所示，过点D作DE⊥AB于点E，则DE=4。因为AD平分∠BAC，∠ACB=90°，DE⊥AB。所以 DC=DE =4，所以BD=BC-DC=10-4=6。
如图，已知∠AOB，如何作出它的平分线?假设∠AOB的平分线已作出，请回答下列问题：（1）这条射线有什么特征?（2）如何确定这条射线上除端点之外的一个点?
知识点2 用尺规作角的平分线
线上的点到这个角的两边的距离相等。需要确定的点是角的对称轴上的点，因此应当从角两边进行“对称”的操作。
你能解释这样做的道理吗？如何证明？
例2 观察图中尺规作图痕迹，下列说法错误的是（　　）A．OE是∠AOB的平分线 B．OC=ODC．点C、D到OE的距离不相等 D．∠AOE=∠BOE
解：根据尺规作图的画法可知：OE是∠AOB的角平分线。A．OE是∠AOB的平分线，正确；B．OC=OD，正确；C．点C、D到OE的距离相等，不正确；D．∠AOE=∠BOE，正确。
回顾·反思 研究等腰三角形、线段、角的过程，你运用了哪些方法?积累了哪些经验?
研究等腰三角形、线段、角的过程主要运用了动手操作、画图、尺规作图、小组合作交流等方法。积累了观察与猜想、逻辑推理与证明、分类讨论归纳总结、应用与拓展、反思与提升等活动经验。
1.如图，OC平分∠AOB，点P在OC上，PD⊥OB，PD=2，则点P到OA的距离是( )A.4 B.3 C.2 D.1解析:如图，过P作PE⊥AO于点E，因为OC平分∠AOB，点P在OC上，PD⊥OB，所以PE=PD=2D。所以点P到OA的距离是2。
2.如图，BD是Rt△ABC的一条角平分线，DE⊥AB，垂足为E。你认为DE与DC相等吗?为什么?
解:DE=DC。因为BD是Rt△ABC的角平分线，DE⊥AB，DC⊥BC，所以DE=DC。
3.任意画一个角，用尺规将它四等分。
先画∠AOB的角平分线OC再画∠AOC和∠COB的角平分线分别是OD、OE。
4.在△ABC中，∠C=90°，AD是∠BAC的平分线，DE⊥AB于点E，点F在AC上， CF=EB。试说明： BD=DF。