数学七年级下册（2024）第六章 变量之间的关系3 用关系式表示变量之间的关系图片课件ppt

这是一份数学七年级下册（2024）第六章 变量之间的关系3 用关系式表示变量之间的关系图片课件ppt，共16页。PPT课件主要包含了学习目标，新课导入，新知探究，解y3x，含自变量的代数式，自变量x，因变量y，因变量，系数为1，解能确定等内容，欢迎下载使用。
1.理解两个变量之间的关系可以用关系式表示，能在一个关系式中指出自变量和因变量。2.能够在具体的情境中列出表示变量之间关系的关系式。【重难点】
能确定一个三角形的面积的量有哪些？
三角形的底边长和对应的高。
(1)在这个变化过程中，自变量、因变量各是什么？当底边长减小时，三角形的面积是如何变化的？
知识点：用关系式表示变量之间的关系
如图，△ABC的底边BC上的高是6cm。当三角形的顶点C沿底边所在直线向点B运动时，三角形的面积发生了变化。
解：自变量是三角形的底边长，因变量是三角形的面积。 减小。
(2)如果三角形的底边长为x(单位：cm)，那么三角形的面积y(单位：cm2)如何表示？
(3)当底边长从12cm变化到3cm时，三角形的面积从 cm2变化到 cm2。
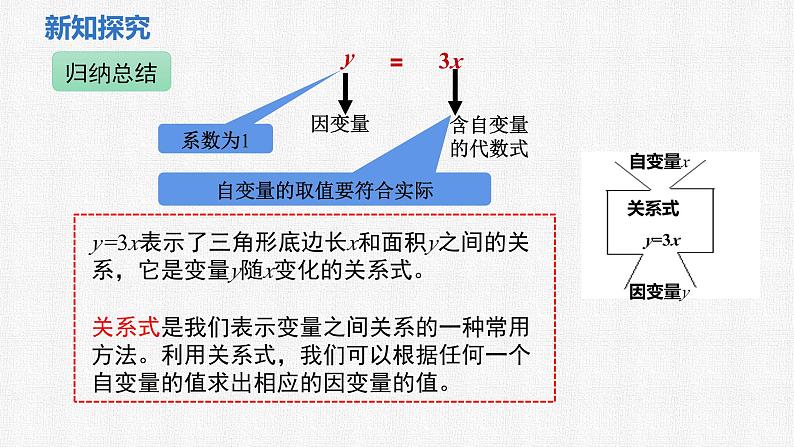
y=3x表示了三角形底边长x和面积y之间的关系，它是变量y随x变化的关系式。关系式是我们表示变量之间关系的一种常用方法。利用关系式，我们可以根据任何一个自变量的值求出相应的因变量的值。
关系式 y=3x
自变量的取值要符合实际
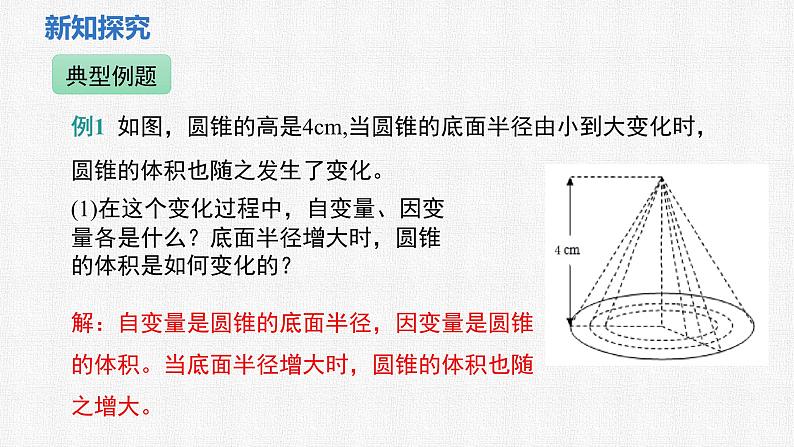
例1 如图，圆锥的高是4cm,当圆锥的底面半径由小到大变化时，圆锥的体积也随之发生了变化。
解：自变量是圆锥的底面半径，因变量是圆锥的体积。当底面半径增大时，圆锥的体积也随之增大。
(1)在这个变化过程中，自变量、因变量各是什么？底面半径增大时，圆锥的体积是如何变化的？
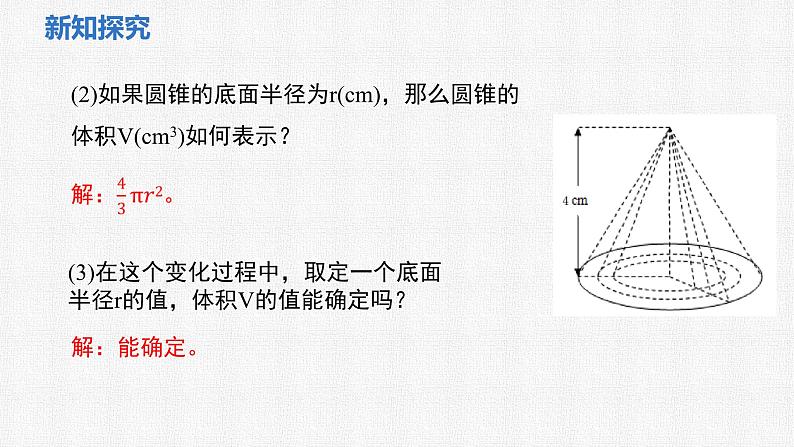
(2)如果圆锥的底面半径为r(cm)，那么圆锥的体积V(cm3)如何表示？
(3)在这个变化过程中，取定一个底面半径r的值，体积V的值能确定吗？
优点：简单明了，能准确反映整个变化过程中自变量与因变量的相互关系。缺点：求对应值时有时要经过比较复杂的计算，而且实际问题中，有的变量之间的关系不一定能用关系式表示出来。
用关系式表示变量之间的关系：
例2 你知道什么是“低碳生活”吗？ “低碳生活”是指人们生活中尽量减少所耗能量，从而降低碳(特别是二氧化碳)的排放量的一种生活方式。
一些常见的二氧化碳排放量计算公式如下表所示：
（1）用字母表示家居用电的二氧化碳排放量的公式_ ___，其中的字母表示_ _。
（2）在上述关系式中，用电量每增加1kW·h，二氧化碳排放量增加_ _。当用电量从1kW·h增加到100kW·h时，二氧化碳排放量从_ 增加到_ __。
用电量（x）和二氧化碳排放量（y）
（3）小明家本月用电大约110kW·h、天然气20m³、自来水5t、耗油75L，请你计算一下小明家这几项的二氧化碳排放量总和。
解：110×0.785+20×0.19+5×0.91+75×2.7=86.35+3.8+4.55+202.5=297.2（kg）。答：小明家这几项的二氧化碳排放量总和是297.2kg。
1.变量x与y之间的关系式是y=x2-3，当自变量x=2时，因变量y的值是( )
A.－2 B.－1 C.1 D.2
2.如图是一个简单的数值运算程序，当输入x的值为-1时，则输出的y的值为___。
3.在关系式s=40t中，当t=1.5时，s=_ _。
求变量之间的关系式的“三途径”：1.根据表格中所列的数据，归纳总结两个变量之间的关系式；2.利用公式写出两个变量之间的关系式，比如各类几何图形的周长、面积、体积公式等；3.结合实际问题写出两个变量之间的关系式，比如“销量×(售价－进价)=利润”等。
1.如图，长方形铁板的长为a，在左侧截掉一个最大的正方形。若剩余部分的周长为b，则a与b之间的关系可以表示为( 　　)
A．b＝2a B．b＝2a+2C．b＝4a D．b＝4a﹣4
2.如图，是若干个粗细均匀的铁环最大限度的拉伸组成的链条，已知每个铁环长4厘米，铁环粗0.5厘米，铁环间处于最大限度的拉伸状态。设x个铁环长为y厘米，则y与x之间的关系式为　 　。
3.用100m长的篱笆在地上围成一个矩形，当矩形的宽由小到大变化时，矩形的面积也随之发生变化。 (1)在这个变化过程中，自变量、因变量各是什么？
(3)当矩形的宽由1m变化到25m时，矩形面积由y1(m2)变化到y2(m2)，求y1和y2的值。
解：在这个变化过程中，自变量是矩形的宽，因变量是矩形的面积。
解：当x＝1时，y1＝－12＋50×1＝49;当x＝25时，y2＝－252＋50×25＝625。
(2)设矩形的宽为x(m)，求矩形的面积y(m2)与x的关系式；