初中青岛版（2024）6.2 平行四边形的判定备课课件ppt

这是一份初中青岛版（2024）6.2 平行四边形的判定备课课件ppt，共19页。PPT课件主要包含了第六章平行四边形，青岛版八年级数学下册，第一课时，学习目标，观察与思考，提出问题，画图探究，推理论证，证明连结AC，∵AD∥BC等内容，欢迎下载使用。
6.2 平行四边形的判定
探究、理解并掌握用边来判定平行四边形的方法
会综合运用平行四边形的判定与性质解决问题
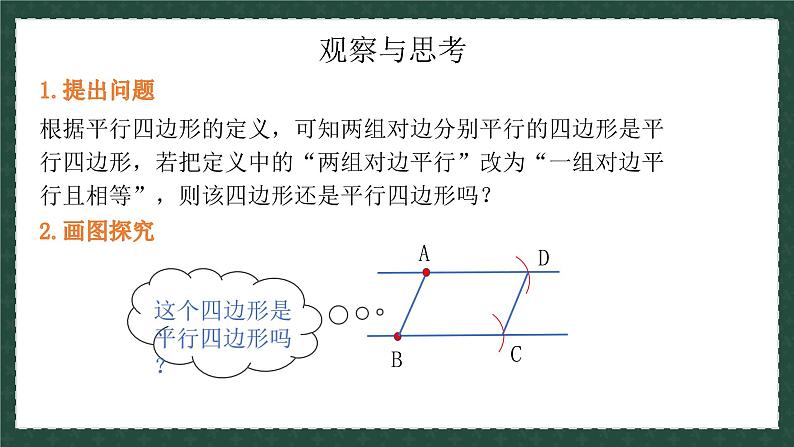
根据平行四边形的定义，可知两组对边分别平行的四边形是平行四边形，若把定义中的“两组对边平行”改为“一组对边平行且相等”，则该四边形还是平行四边形吗？
已知：如图，在四边形ABCD中，AD∥BC，且AD＝BC　求证：四边形ABCD是平行四边形。
∴四边形ABCD是平行四边形
∵AD=BC,AC=CA
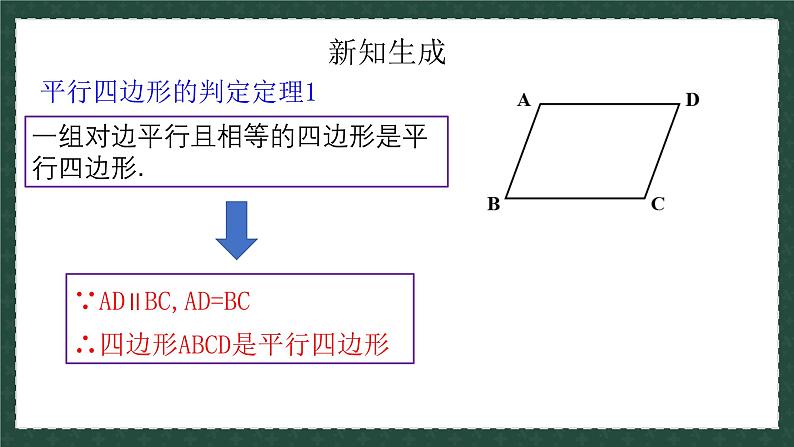
一组对边平行且相等的四边形是平行四边形.
平行四边形的判定定理1
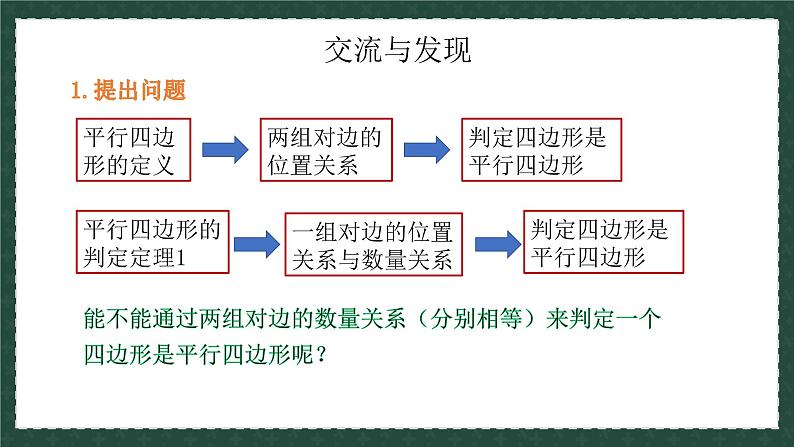
能不能通过两组对边的数量关系（分别相等）来判定一个四边形是平行四边形呢？
2.大家仿照刚才的探究方法进行自主探究.
学习指导：（1）在自学过程中，试着解决以下问题 ①如何画出满足条件的四边形？ ②如何证明画出的四边形是平行四边形？ ③通过探究得出什么结论？（2）时间约3分钟,3分钟后由学生进行展示
∵AB=CD,AD=BC，AC=AC∴△ABC≌△ADC
两组对边相等的四边形是平行四边形.
平行四边形的判定定理2
思考：平行四边形的判定定理2与平行四边形的性质定理1有什么关系？
例1：如图，E,F,G,H分别是平行四边形ABCD的边AD,AB,BC,CD上的点，且AE=CG,BF=DH.求证：四边形EFGH是平行四边形。
证明：∵四边形ABCD是平行四边形∴∠A=∠C,AB=CD
∵BF=DH∴AF=CH
∵AE=CG∴△AFE≌△CHG∴EF=GH
∴四边形EFGH是平行四边形
1.已知：如图，E,F分别是平行四边形ABCD的边AD,BC的中点.利用判定定理1和2证明四边形BEDF是平行四边形.
2.如图:在四边形ABCD中,∠ADB=∠CBD，∠ABD=∠CDB.利用三种方法证明四边形ABCD是平行四边形.
方法一∵∠ADB=∠CBD∴AD∥BC∵∠ABD=∠CDB∴AB∥CD∴四边形ABCD是平行四边形.
方法二∵∠ADB=∠CBD∴AD∥BC∵∠ABD=∠CDB,BD=BD∴△ABD≌△CBD∴AD=BC∴四边形ABCD是平行四边形.
方法三∵∠ABD=∠CDB,∠ADB=∠CBDBD=BD∴△ABD≌△CBD∴AD=BC，AB=CD∴四边形ABCD是平行四边形.
3.已知：如图，在平行四边形ABCD中，AE、CF分别是∠DAB、∠BCD的平分线．求证：四边形AFCE是平行四边形．
4.如图，在平行四边形ABCD中，点E，F是对角线AC上的两点，且AF=CE.求证：四边形BEDF是平行四边形.
∵四边形ABCD是平行四边形∴AB∥CD∴∠DCE=∠BAF∵AB=CD,AF=CE∴△ABF≌△DCE∴BF=DE同理:BE=DF∴四边形BEDF是平行四边形.
3.如图，在平行四边形ABCD中，点E、F分别在AB、CD上，AE=CF. 四边形DEBF是平行四边形吗？为什么？
四边形DEBF是平行四边形
1.下列不能判断四边形ABCD是平行四边形的是（ ）
A.两组对边平行的四边形是平行四边形B.一组对边平行且相等的四边形是平行四边形C.两组对边相等的四边形是平行四边形D.一组对边相等，另一组对边平行的四边形是平行四边形