





所属成套资源:苏科版数学九年级上学期课件PPT整套
数学九年级上册2.3 确定圆的条件优秀课件ppt
展开
这是一份数学九年级上册2.3 确定圆的条件优秀课件ppt,共34页。PPT课件主要包含了位置关系,有且只有,外接圆,△ABC,垂直平分线,三个顶点,A锐角三角形,B直角三角形,C钝角三角形,D等腰三角形等内容,欢迎下载使用。
1.会过不在同一直线上的三个点作一个圆;2.了解三角形的外接圆,三角形的外心,圆的内接三角形的概念.
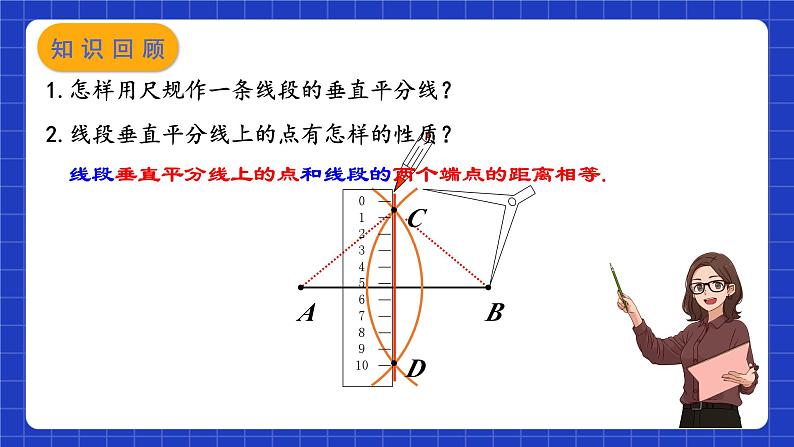
1.怎样用尺规作一条线段的垂直平分线?
2.线段垂直平分线上的点有怎样的性质?
线段垂直平分线上的点和线段的两个端点的距离相等.
哥哥应该带哪一块玻璃碎片去商店配制?
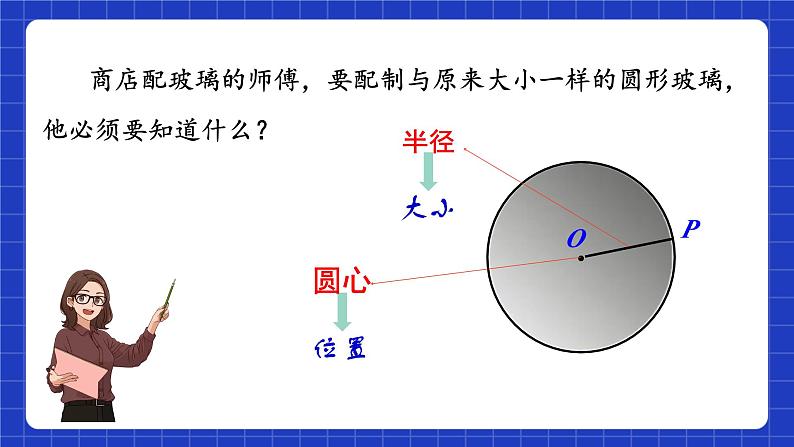
商店配玻璃的师傅,要配制与原来大小一样的圆形玻璃,他必须要知道什么?
在碎片上任意取一个点能确定这个圆吗?
经过一个已知点能作无数个圆
在碎片上任意取两个点能确定这个圆吗?
经过两个已知点能作无数个圆
在碎片上任意取三个点能确定这个圆吗?
如何过不在同一直线的三个点作一个圆呢?
假设经过A、B、C三点的⊙O存在.
(1)圆心O到A、B、C三点距离______(填“相等”或”不相等”),所以圆心O在线段AB、AC 、BC的_____________上.
(2)连结AB、AC,过O点分别作直线MN⊥AB, EF⊥AC,则MN是AB的___________;EF是AC的______________,交点O到B、C的距离______.
已知:不在同一直线上的三点A、B、C.求作:⊙O使它经过点A、B、C.
作法:1. 连结AB,作线段AB的垂直平分线MN;2. 连接AC,作线段AC的垂直平分线EF,交MN于点O;3. 以O为圆心,OB为半径作圆.所以⊙O就是所求作的圆.
经过不在同一直线的三个点能确定一个圆.
经过在同一直线的三个点能作圆吗?为什么?
在同一直线上的三点不能作圆
不在同一条直线上的三点确定一个圆.
三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的________, ________是⊙O的内接三角形,____是△ABC的外心.
外心是△ABC三条边的_____________的交点, 它到三角形的__________的距离相等.
现在你知道哥哥应该带哪一块玻璃碎片去商店配制了吗?
商店配玻璃的师傅如何根据这块碎片确定原来圆的大小呢?
方法:1. 在圆弧上任取三点A、B、C;2. 作线段AB、BC的垂直平分线,其交点O即为圆心;3. 以点O为圆心,OA长为半径作圆,⊙O即为所求.
(1)经过三点一定可以作圆.( )(2)三角形的外心就是这个三角形两边垂直平分线的交点.( )(3)三角形的外心到三边的距离相等.( )(4)等腰三角形的外心一定在这个三角形内.( )
例1 画出以下三角形的外接圆,并指出三角形外心所在的位置.
(1)比较这三个三角形外心的位置,你有何发现?
锐角三角形的外心在三角形的内部;直角三角形的外心在三角形的一条边(斜边上),并且这个点是斜边的中点;钝角三角形的外心在三角形的外部.
(2)图②中,若AB=3,BC=4,则它的外接圆半径是多少?
例2 某地区有A、B、C三所学校,如图所示,今要盖一个图书馆提供给三个学校的学生的使用,为了公平起见,图书馆的位置应该盖在哪里?才能使三个学校到图书馆的距离相等.
解:如图所示:(1)在圆弧上任取三点A、B、C;(2)作线段AC、 BC的垂直平分线,其交点O即为圆心.
2.已知AB=4cm,作半径为 3cm 的圆,使它经过A、 B两点,这样的圆能作多少个?
解:这样的圆能画2个.如图:①作AB的垂直平分线l,再以点A为圆心,3cm为半径作圆交l于O1和O2;②分别以O1和O2为圆心,以3cm为半径作圆,则⊙O1和⊙O2为所求.
解:这样的圆能画1个.如图:作AB的垂直平分线l,交AB于O点,然后以O为圆心,以2cm为半径作圆,则⊙O即为所求.
变式:已知AB=4cm,作半径为 2cm 的圆,使它经过A、 B两点,这样的圆能作多少个?
3.如图,在四边形ABCD中,∠A=∠C=90,(1)经过点A、B、D三点作⊙O;(2)⊙O是否经过点C?请说明理由.
解:(1)如图,⊙O就是所要求作的圆.(2)点C在⊙O上.理由如下: 连结OC,∵⊙O为△BDA的外接圆,而∠BAD=90°,∴BD为⊙O的直径.∵点O为BD的中点,∠BCD=90°,∴OC为斜边BD上的中线,∴OC=OB=OD,∴点C在⊙O上.
不在同一直线上的三个点确定一个圆
三角形的外心到三角形的三个顶点的距离相等.
经过三角形的三个顶点的圆叫做三角形的外接圆
外接圆的圆心叫三角形的外心
1. 下列说法中,正确的是( )A.过两点一定可以作一个且只可以作一个圆B.过三点一定可以作一个且只可以作一个圆C.过不在同一直线上的三点一定可以作一个且只可能作一个圆D.过不在同一直线上的四点一定可以作一个且只可能作一个圆
2. 下列命题中,假命题的个数为( )①三角形只有一个外接圆;②钝角三角形的外心在三角形外部;③等边三角形的外心也是三角形的三条中线、高、角平分线的交点④直角三角形的外心是斜边的中点.A.0 B.1 C.2 D.3
3. 给定下列条件可以确定一个圆的是( )A.已知圆心 B.已知半径的长C.已知直径的长 D.不在同一条直线上的三个点
4.三角形的外心是三角形中( )A.三条高的交点 B.三条中线的交点C.三条角平分线的交点 D.三边垂直平分线的交点
5.三角形的外心具有的性质是( )A.到三边的距离相等 B.到三个顶点的距离相等C.外心在三角形外 D.外心在三角形内
6.若一个三角形的外心在它的外部,则该三角形一定是( )
8.直角三角形的两边长分别为16、12,则此三角形的外接圆的半径为 10或8 .
9.如图,点 A、B、C均在6×6的正方形网格的格点上,过A、B、C三点的圆除经过A、B、C三点外,还能经过的格点个数为 5 .
10.图中工具的CD边所在直线恰好垂直平分AB边,怎样用这个工具找出一个圆的圆心.
11.如图,点O是△ABD的外心,∠OBC=30°,连接DO并延长,交AB于点C,连接OA,∠AOC=36°,求∠DOB的度数.
解:∵点O是△ABD的外心,∴OA=OB.∴∠OAC=∠OBC=30°.又∵∠AOC=36°,∴∠OCB=∠AOC+∠OAC=36°+30°=66°.∴∠DOB=∠OCB+∠OBC=66°+30°=96°
12. 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,EF是AC的垂直平分线,交AD于点O.若AB=4,OF=1,求△ABC的外接圆的面积.
相关课件
这是一份初中数学苏科版九年级上册2.3 确定圆的条件课文课件ppt,共16页。PPT课件主要包含了三角形的外接圆,圆的内接三角形,试一试,交流与小结,练习拓展等内容,欢迎下载使用。
这是一份初中数学苏科版九年级上册2.3 确定圆的条件评优课ppt课件,共33页。PPT课件主要包含了垂直平分线,不能圆心不能确定,位置关系,有且只有,外接圆,△ABC,三个顶点,●O1,●O2,过一点可以作无数个圆等内容,欢迎下载使用。
这是一份苏科版九年级上册2.3 确定圆的条件获奖课件ppt,共22页。PPT课件主要包含了3确定圆的条件,操作与思考,确定是圆的条件,三点确定一个圆,内接三角形,习题23等内容,欢迎下载使用。










