初中数学新北师大版七年级上册3问题解决策略：归纳教学课件2024秋

这是一份初中数学新北师大版七年级上册3问题解决策略：归纳教学课件2024秋，共17页。
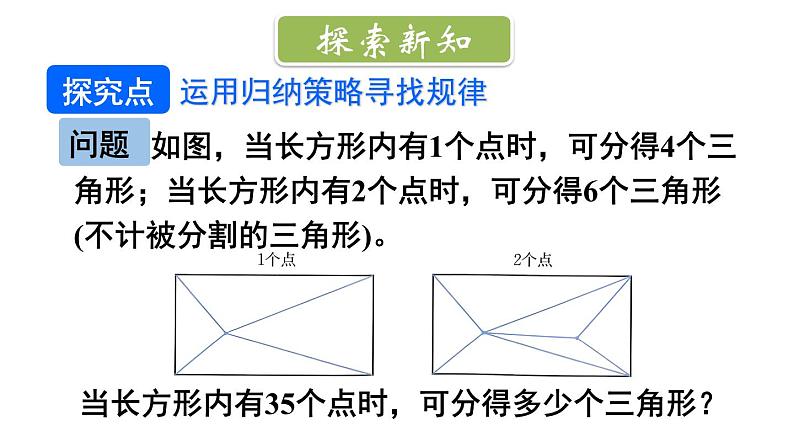
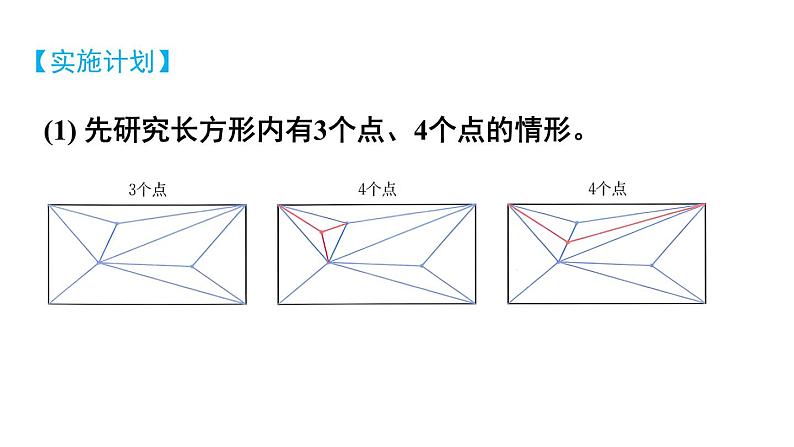
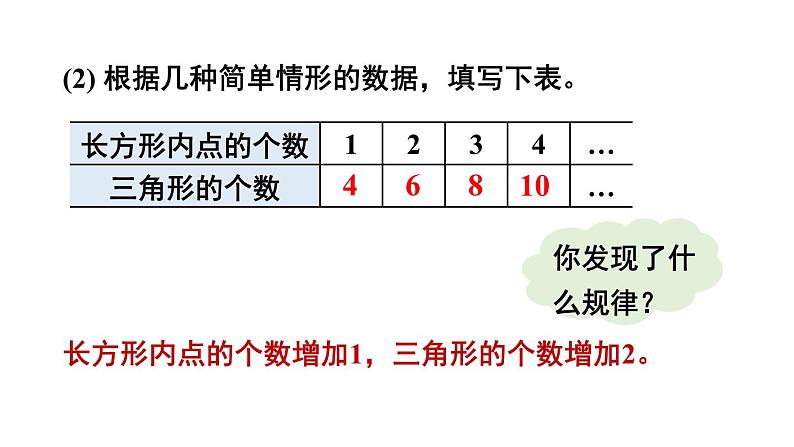
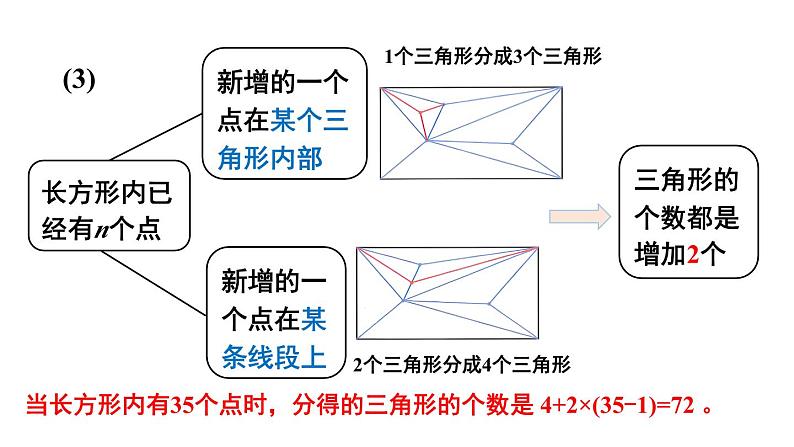
问题解决策略：归纳北师大版·七年级上册状元成才路情境引入探索新知当长方形内有35个点时，可分得多少个三角形？【理解问题】(1) 先动手试试，感受分割得到三角形的过程。(2) 已知条件是什么？目标是什么？已知条件：长方形内有35个点，将这些点按照 前面的方法连接，形成多个三角形。目标：求出分得的三角形的总个数。【拟定计划】(1) 直接研究“长方形内有35个点”的情形， 你遇到了什么困难？(2) 哪些情形容易研究？从中你能发现什么规律？(3) 你发现的规律正确吗？你能给出合理的解释吗？点太多，不方便将三角形全部画出来。点的个数较少时容易研究。【实施计划】(1) 先研究长方形内有3个点、4个点的情形。(2) 根据几种简单情形的数据，填写下表。46810长方形内点的个数增加1，三角形的个数增加2。(3)长方形内已经有n个点1个三角形分成3个三角形2个三角形分成4个三角形三角形的个数都是增加2个当长方形内有35个点时，分得的三角形的个数是 4+2×(35-1)=72 。【回顾反思】(1) 如果长方形内有100个点呢？一般地，如果长方形内有n个点呢？4+2×(100-1)=2024+2×(n-1)=2n+2(2) 你还能提出并解决什么问题？(3) 从简单的情形开始思考有什么好处？通过简单情形归纳一般性结论，你有哪些经验?在简单情形中寻找规律例1.32024的个位数字是多少？31=332=933=2734=8135=24336=72937=218738=6561……3n (n为正整数)的个位数字按3，9，7，1四个数字循环出现。2024÷4=506，32014的个位数字是 1。2. 如图，将一根绳子折成三段，然后按如图所示方式剪开。剪1刀，绳子变为4段；剪2刀，绳子变为7段。(1) 剪12刀，绳子变成多少段？(2) 有可能正好剪得101段吗？1刀 4 段2刀 7 段3刀 10 段4刀 13 段…….…….n 刀 (3n+1) 段2. 如图，将一根绳子折成三段，然后按如图所示方式剪开。剪1刀，绳子变为4段；剪2刀，绳子变为7段。(1) 剪12刀，绳子变成多少段？(2) 有可能正好剪得101段吗？(1) 剪12刀，绳子变成3×12+1=37 (段)(2) 不可能。(1) 第10行的10个数的和是多少？(2) 你还能找到其他规律吗？试一试！解：(1) 103 =1000【教材P103~104 第3题】1.由1，3，5，7，9，11，13，15，17，19，…组成的三角形数阵如下图所示。(2)第n行的第1个数：n2-n+1第n行的第n个数：n2+n-12.某类简单化合物中前6种化合物的分子结构模型如下图所示，其中灰球代表碳原子，白球代表氢原子。按照这一规律，第60种化合物的分子结构模型中有多少个氢原子？4+2×(60-1)=122(个)【教材P103 第4题】课堂总结1.为了解决问题，我们是从什么情形入手的?2.从简单情形中找出某种规律后，是否就说明找到了一般性规律?还需要注意什么?3.要想归纳出一般性结论，我们一般要经过哪些步骤?