



所属成套资源:【新课标专题训练】北师大版数学九年级下册同步课件+考点专题训练
北师大版(2024)九年级下册6 直线与圆的位置关系完美版ppt课件
展开
这是一份北师大版(2024)九年级下册6 直线与圆的位置关系完美版ppt课件,共28页。PPT课件主要包含了知识要点,跟踪练习,数形结合,位置关系,数量关系,公共点个数,典型例题,还有其他解答方法吗,相切或相交,有dr等内容,欢迎下载使用。
1.经历探索直线和圆位置关系的过程.2.理解直线与圆有相交、相切、相离三种位置关系.(重点)3.了解切线的概念,探索切线与过切点的直径之间的关系.(难点)
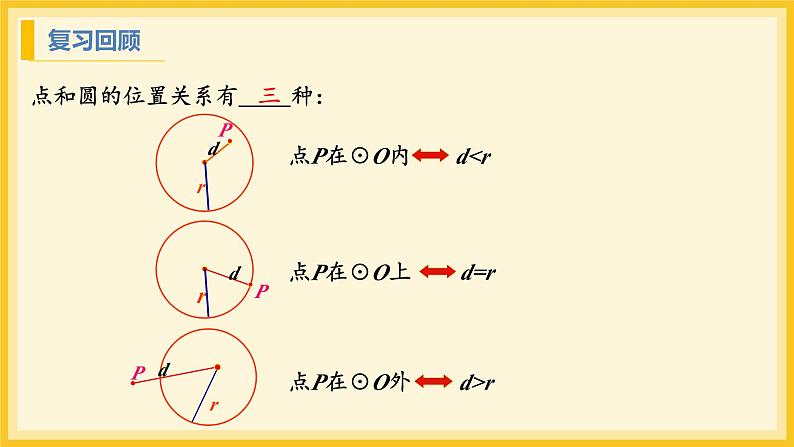
点和圆的位置关系有 种:
如图,如果我们把太阳看作一个圆,把地平线看作一条直线,太阳升起的过程中,太阳和地平线会有几种位置关系?
观察三幅太阳升起的照片,地平线与太阳的位置关系是怎样的?
探究一:直线和圆的位置关系
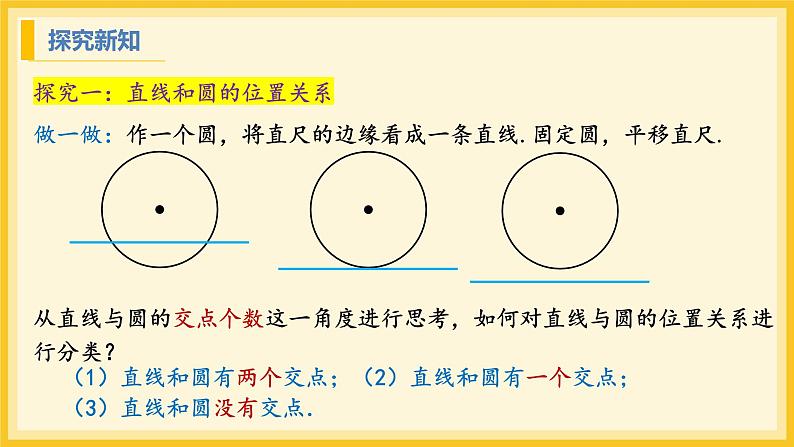
做一做:作一个圆,将直尺的边缘看成一条直线.固定圆,平移直尺.
从直线与圆的交点个数这一角度进行思考,如何对直线与圆的位置关系进行分类?
(1)直线和圆有两个交点;(2)直线和圆有一个交点;(3)直线和圆没有交点.
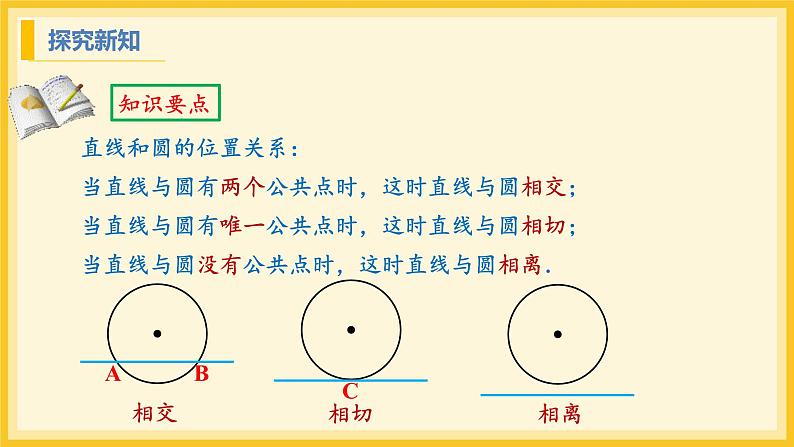
直线和圆的位置关系:当直线与圆有两个公共点时,这时直线与圆相交;当直线与圆有唯一公共点时,这时直线与圆相切;当直线与圆没有公共点时,这时直线与圆相离.
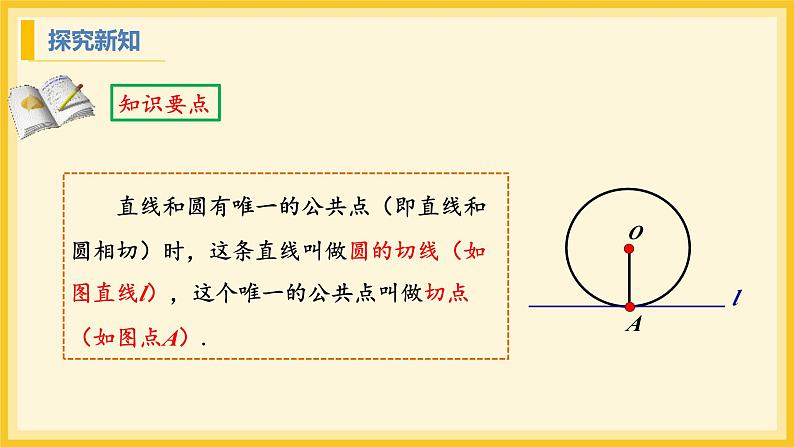
直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的切线(如图直线l),这个唯一的公共点叫做切点(如图点A).
判断下列说法是否正确:直线与圆最多有两个公共点.( )若直线与圆相交,则直线上的点都在圆上. ( )若A是☉O上一点,则直线AB与☉O相切. ( )④若C为☉O外一点,则过点C的直线与☉O相交或相离.( ) ⑤直线a 和☉O有公共点,则直线a与☉O相交.( )
用圆心O到直线的距离d与圆的半径r的关系来揭示圆和直线的位置关系.
探究二:圆的切线的性质
三个图形都是轴对称图形,对称轴经过圆心且与直l线垂直.
直径AB垂直于直线CD.
理由是:∵右图是轴对称图形,AB所在直线是对称轴,∴沿直线AB对折图形时,AC与AD重合,∴∠BAC=∠BAD=90°.∴AB⊥CD
几何语言:∵直线l是⊙O 的切线,A是切点,∴直线l ⊥OA.
切线性质定理: 圆的切线垂直于过切点的半径.
提示:(1)要使AB与⊙C相切,则过点C作AB的垂线,垂足为D,求出CD的长即可;(2)根据直线与圆的位置关系进行判断.
1.已知⊙O的直径等于12cm,圆心O到直线l的距离为5cm,则直线l与⊙O的交点个数为( ) A.0 B.1 C.2 D.无法确定
3. 已知⊙O半径R=3,O点到l的距离为d,且d是方程x2-5x+6=0的一个根,则l与⊙O的位置关系是 .
解:过C作CD⊥AB,垂足为D.
∴当半径长为2.4cm时,AB与圆C相切.
(2)以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?① r=2cm;② r=2.4cm; ③ r=3cm.
解:由(1)可知圆心C到AB的距离d=2.4cm.
所以 ①当r=2cm时,
②当r=2.4cm时,有d=r.
③当r=3cm时,有d 5 C. r = 5 D. r ≥ 5
3. ⊙O的最大弦长为8,若圆心O到直线l的距离为d=5,则直线l与⊙O .
(2)解:由(1)可知OA=OC=AC, ∴△OAC为等边三角形, ∴∠AOB=60°, ∴在Rt△OAB中, ∠B=90°-60°=30°.
教材习题3.7.
相关课件
这是一份初中数学北师大版九年级下册第三章 圆6 直线与圆的位置关系备课ppt课件,共30页。PPT课件主要包含了位置关系,公共点个数,填一填,知识要点,判一判,直线和圆相交,直线和圆相切,直线和圆相离,数形结合,数量关系等内容,欢迎下载使用。
这是一份北师大版九年级下册1 圆授课课件ppt,共19页。PPT课件主要包含了情境导课,新知探究,直线和圆相切,直线和圆相交,d>r,d<r,归纳新知,练习巩固,小结与作业等内容,欢迎下载使用。
这是一份初中数学北师大版九年级下册1 圆课堂教学课件ppt,共29页。PPT课件主要包含了知识回顾,归纳总结,随堂演练等内容,欢迎下载使用。











