初中6 直线与圆的位置关系说课课件ppt

这是一份初中6 直线与圆的位置关系说课课件ppt，文件包含36直线和圆的位置关系第2课时pptx、北师大版数学九年级下册第三章第6节练练基础题docx、北师大版中学数学九年级下册第三章圆36直线和圆的位置关系第2课时教学详案docx等3份课件配套教学资源，其中PPT共26页， 欢迎下载使用。

1.理解并掌握切线的判定定理,能够熟练运用切线的性质和判定解决有关的证明和计算.（重点） 2.了解三角形的内切圆的有关概念及性质并能灵活应用.（重点）
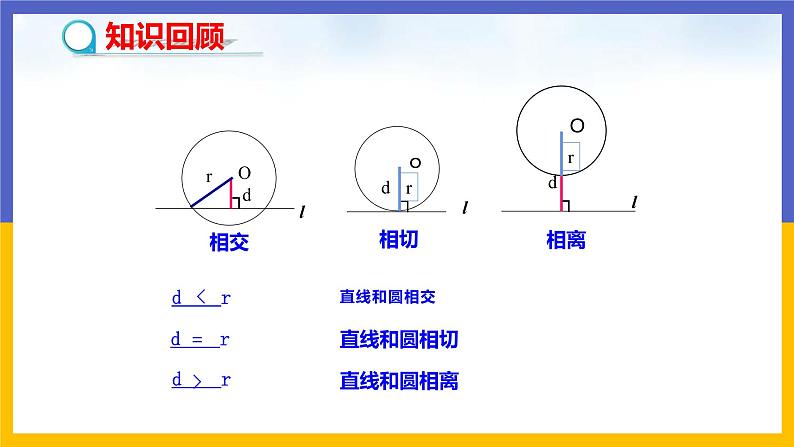
你能写出一个命题来表述这个事实吗?
探究1 如图,AB是⊙O的直径,直线l经过点A,l与AB的夹角为∠α,当l绕点A顺时针旋转时, 圆心O到直线l的距离d如何变化？
过半径外端且垂直于半径的直线是圆的切线.
∵AB是⊙O的直径,直线CD经过A点,且CD⊥AB,∴ CD是⊙O的切线.
这个定理实际上就是d=r 直线和圆相切的另一种说法.
例1.如图,AB是⊙O的直径, ∠ABT=45°,AT=BA．求证:AT是⊙O的切线.
证明：AT经过直径的一端，因此只要证AT垂直于AB即可，而由已知条件可知AT=AB，所以∠ABT＝∠ATB，又由∠ABT＝45°，所以∠ATB=45°.由三角形内角和定理可证∠TAB=90°，即AT⊥AB，故AT是⊙O的切线．
1.如图,已知直线AB 经过⊙O上的点C, 并且AO=OB,CA=CB,那么直线 AB是⊙O的切线吗?
解：连接OC，C为半径的外端，因此只要证OC垂直于AB即可，而由已知条件AO=OB，所以∠A＝∠B，又由AC＝BC，所以OC⊥AB．∴直线AB是⊙O的切线.
2．如图,已知：OA=OB＝５,AB＝８，以O为圆心，以3为半径的圆与直线AB相切吗？为什么？
解：过O作OC⊥AB ，因此只要证OC=3即可,而由已知条件可知AO=OB=5，AB=8，所以AC＝BC=4，据勾股定理得OC=3.∴ ⊙O与直线AB相切.
探究2 如图，在△ABC中，作一个圆使它与这个三角形的三边都相切.
（1）作∠ABC,∠ACB的平分线BM和CN，交点为I.（2）过点I作ID⊥BC，垂足为D.（3）以I为圆心，ID为半径作⊙I， ⊙I就是所求的圆.
∵BE和CF只有一个交点I,并且点I到△ABC三边的距离相等,
因此和△ABC三边都相切的圆可以作出一个,并且只能作一个.
定义：与三角形三边都相切的圆叫做三角形的内切圆. 内切圆的圆心叫做三角形的内心，是三角形三条角平分线的交点.
这样的圆可以作出几个呢?为什么?
分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明它们内心的位置情况.
判断题：1.三角形的内心到三角形各个顶点的距离相等（ ）2.三角形的外心到三角形各边的距离相等 （ ）3.等边三角形的内心和外心重合（ ）4.三角形的内心一定在三角形的内部（ ）
例2.如图，在△ABC中，点O是内心， （1）若∠ABC=50°，∠ACB=70°，则∠BOC的度数是 .
（2）若∠A=80°，则∠BOC= . （3）若∠BOC=110°，则∠A= .
1.已知:如图,⊙O是Rt△ABC的内切圆,∠C是直角, AC=3,BC=4.求⊙O的半径r .
解：由Rt△ABC的三边长与其内切圆半径间的关系得
2.如图，某乡镇在进入镇区的道路交叉口的三角地处建造了一座镇标雕塑，以树立起文明古镇的形象.已知雕塑中心M到道路三边AC，BC，AB的距离相等，AC⊥BC，BC=30米，AC=40米.求镇标雕塑中心M离道路三边的距离有多远？
本节课学习了以下内容：
1．探索切线的判定条件．2．作三角形的内切圆．3．了解三角形的内切圆、三角形的内心的概念．
1.如图，点P为△ABC的内心，延长AP交△ABC的外接圆于D，在AC延长线上有一点E，满足AD2＝AB·AE，求证：DE是⊙O的切线.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
证明：连接DC，DO，并延长DO交⊙O于F，连接AF.∵AD2＝AB·AE，∠BAD＝∠DAE，∴△BAD∽△DAE，∴∠ADB＝∠E.　又∵∠ADB＝∠ACB，∴∠ACB＝∠E，BC∥DE，∴∠CDE＝∠BCD＝∠BAD＝∠DAC，又∵∠CAF＝∠CDF，∴∠FDE＝∠CDE+∠CDF＝∠DAC+∠CAF＝∠DAF＝90°，故DE是⊙O的切线.
2.如图，在矩形ABCD中，点O在对角线AC上，以OA的长为半径的圆O与AD，AC分别交于点E，F，且∠ACB=∠DCE．(1)判断直线CE与⊙O的位置关系，并证明你的结论.(2)若tan∠ACB= ，BC=2，求⊙O的半径.
【解析】（1）直线CE与⊙O相切. ∵四边形ABCD是矩形， ∴BC∥AD，∠ACB=∠DAC ， 又 ∵∠ACB=∠DCE，∴∠DAC=∠DCE,连接OE，则∠DAC=∠AEO=∠DCE，∵∠DCE+∠DEC=90°，∴∠AE0+∠DEC=90°，∴∠OEC=90 °， ∴直线CE与⊙O相切.
又∵∠ACB=∠DCE ∴tan∠DCE= ，
设⊙O的半径为r，则在Rt△COE中，
∴DE=DC•tan∠DCE=1，
3.如图,AB是半圆的直径,O为圆心，AD，BD是半圆的弦，且∠PDA=∠PBD.（1）判断直线PD是否为⊙O的切线，并说明理由.（2）如果∠BDE=60°， ，求PA的长.
【解析】（1）PD是⊙O的切线.连接OD,∵OB=OD,∴∠ODB=∠PBD.又∵∠PDA=∠PBD.∴∠ODB=∠PDA.又∵AB是半圆的直径，∴∠ADB=90°.即∠ODB+∠ODA=90°. ∴∠ODA+∠PDA=90°,即OD⊥PD.∴PD是⊙O的切线.
（2）∵∠BDE=60°,∠ODE=90°,∠ADB=90°,∴∠ODB=30°,∠ODA=60°.∵OA=OD,∴△AOD是等边三角形.∴∠POD=60°.∴∠P=∠PDA=30°.在Rt△PDO中，设OD=x,∴
∴x1=1,x2=-1（不合题意，舍去）∴PA=1.
方法归纳证明直线是否是圆的切线有两种辅助线的作法：（1）过圆心作已知直线的垂线，判定距离等于半径；（2）连接圆心与圆上的点，证垂直.