

九年级下册27.2.1 相似三角形的判定授课ppt课件
展开
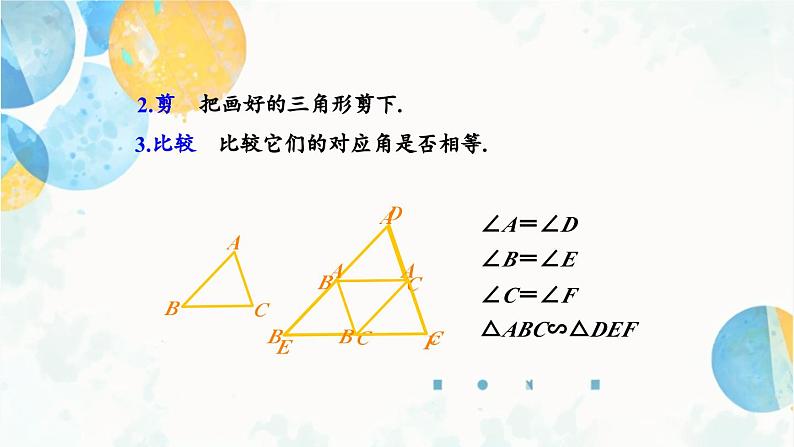
这是一份九年级下册27.2.1 相似三角形的判定授课ppt课件,共20页。PPT课件主要包含了△ABC∽△ADE,任意画一个△ABC,把画好的三角形剪下,∠A=∠D,∠B=∠E,∠C=∠F,△ABC∽△DEF,由此可知,PQ∥EF,∴△DPQ∽△DEF等内容,欢迎下载使用。
1. 掌握利用三边来判定两个三角形相似的方法,并能进行相关计算. 2. 会根据边和角的关系来判定两个三角形相似,并进行相关计算.
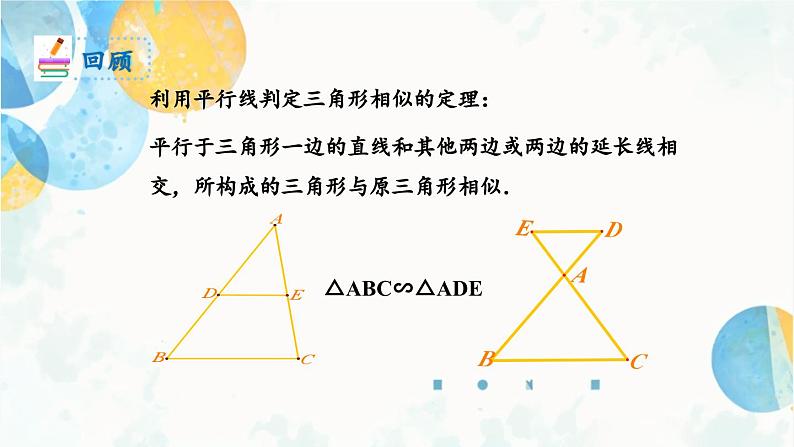
平行于三角形一边的直线和其他两边或两边的延长线相交,所构成的三角形与原三角形相似.
利用平行线判定三角形相似的定理:
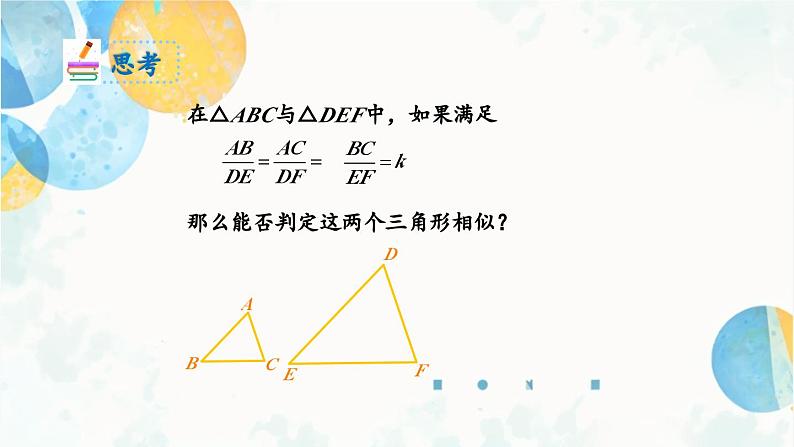
在△ABC与△DEF中,如果满足 那么能否判定这两个三角形相似?
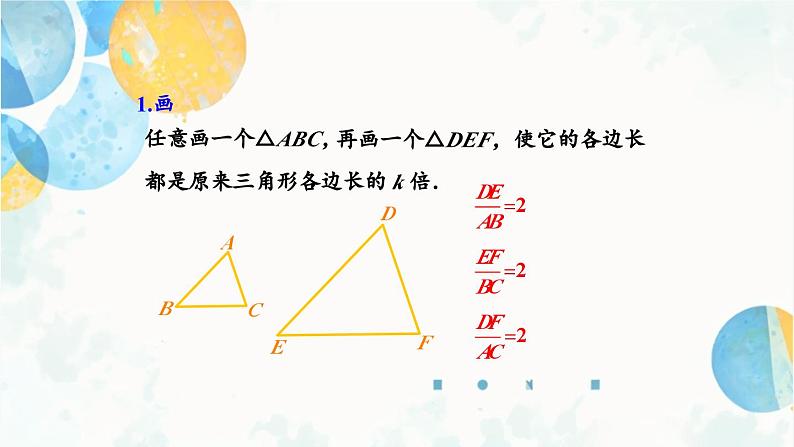
再画一个△DEF,使它的各边长
都是原来三角形各边长的 k 倍.
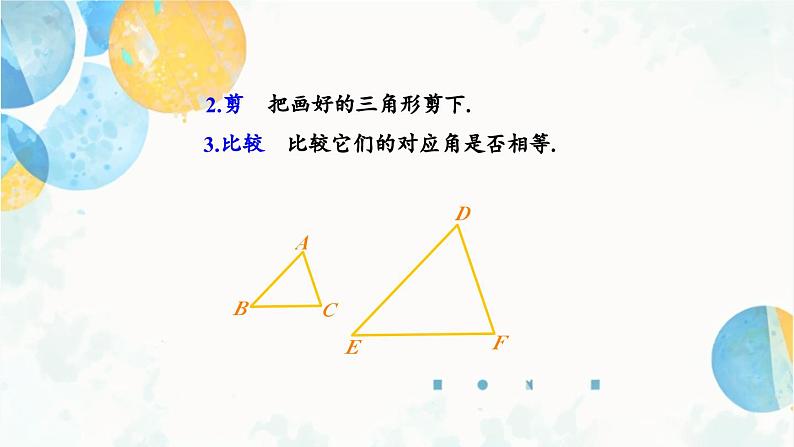
比较它们的对应角是否相等.
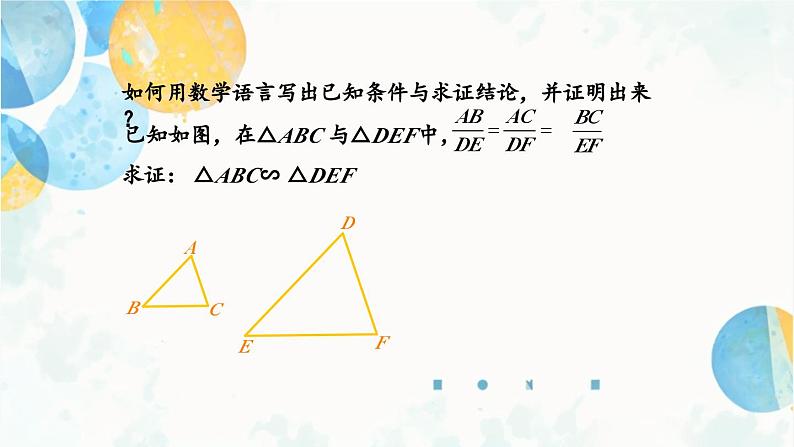
如何用数学语言写出已知条件与求证结论,并证明出来?
已知如图,在△ABC 与△DEF中,
求证: △ABC∽ △DEF
怎样能否在△DEF上作出这样一个△ DPQ呢?怎么作?
证明:在线段DE(或它的延长线)上截取DP=AB,过点P作PQ∥EF,交DF于点Q.根据前面的定理,可得△DPQ∽ △DEF.
∴△DPQ≌△ABC,
∴△ABC∽△DEF.
利用三边判定三角形相似的定理:
三边成比例的两个三角形相似.
求证: △ABC∽ △DEF.
利用两边和夹角判定两个三角形相似的定理:
两边成比例且夹角相等的两个三角形相似.
已知如图,在△ABC与△DEF中, ,
如果把∠A= ∠D,换成∠B =∠E,那么这两个三角形还相似吗?
两边对应成比例且其中一边的对角对应相等的两个三角形不一定相似.
△ABC与△DEF不相似.
1.如图,△ABC中,点 D,E,F 分别是 AB,BC,CA 的中点,求证:△ABC∽△EFD.
∴ △ABC∽△EFD.
证明:∵△ABC中,点D, E, F分别是AB, BC, CA的中点
∴DE= AC ,DF= BC,EF= AB
2.根据下列条件,判断 △ABC 和 △A′B′C′ 是否相似,并说明理由:∠A = 120°,AB = 7 cm,AC = 14 cm,
∠A′ = 120°,A′B′ = 3 cm ,A′C′ = 6 cm.
又 ∠A′ = ∠A,∴ △ABC ∽ △A′B′C′.
相关课件
这是一份初中数学人教版九年级下册27.2.1 相似三角形的判定评优课ppt课件,共20页。PPT课件主要包含了三边+三角,温故知新,三角形相似判定定理1,三角形相似判定定理2,推导格式,新知探究,解相似理由如下,典例精讲,典例练习,解∵ED⊥AB等内容,欢迎下载使用。
这是一份人教版九年级下册27.2.1 相似三角形的判定教学课件ppt,共28页。PPT课件主要包含了温故知新,三角形相似判定定理3,探究新知一,推导格式,知识归纳一,典型例题一,当堂训练一,探究新知二,知识归纳二,典型例题二等内容,欢迎下载使用。
这是一份数学九年级下册27.2.1 相似三角形的判定教学ppt课件,共28页。PPT课件主要包含了第二十七章相似,导入新课,三角形相似判定定理1,三角形相似判定定理2,探究新知一,推导格式,知识归纳一,典型例题一,答案是21,当堂训练一等内容,欢迎下载使用。









