










浙教版(2024)八年级下册4.3 中心对称完美版教学ppt课件
展开《4.3中心对称》是“浙教版八年级数学(下)”第四章第三节的内容.本节课的主要内容是中心对称图形的概念和性质.要求学生了解平行四边形是中心对称图形,了解中心对称图形的性质.要求学生会作与已知图形关于已知点中心对称的图形,能够掌握坐标系中关于原点对称的点的特征.“中心对称图形”是“平移、翻折、旋转”三种基本几何变换中旋转的一种特殊情况,是用运动观点和思想研究图形位置变化或图形性质的数学问题,在教材中有着重要的地位.
1.了解中心对称的概念.2.了解平行四边形是中心对称图形.3.了解中心对称图形的性质.4.会作与已知图形关于已知点中心对称的图形.5.掌握坐标系中关于原点对称的点的特征.
你能在图案中找出一点,使图案绕该点旋转180°后仍和原图案重合吗?
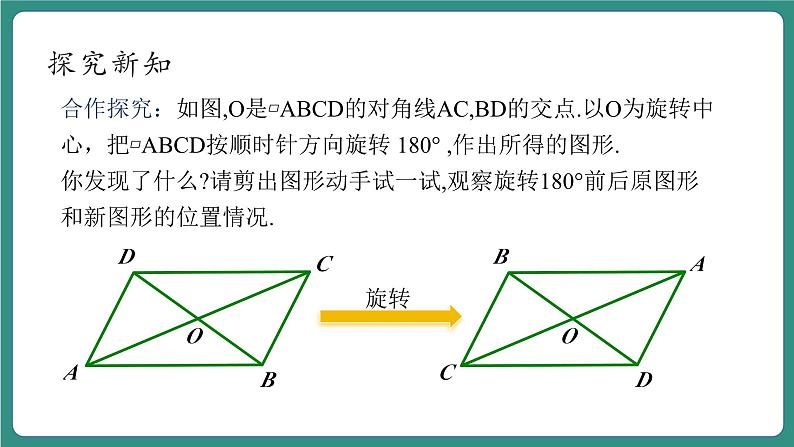
合作探究:如图,O是▱ABCD的对角线AC,BD的交点.以O为旋转中心,把▱ABCD按顺时针方向旋转 180° ,作出所得的图形.你发现了什么?请剪出图形动手试一试,观察旋转180°前后原图形和新图形的位置情况.
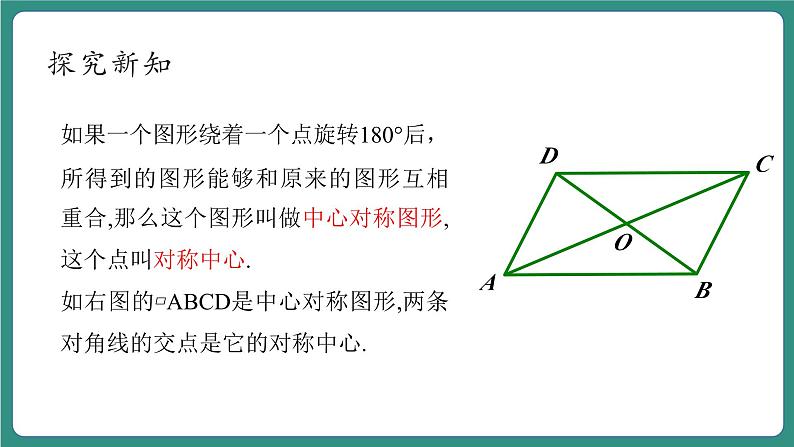
如果一个图形绕着一个点旋转180°后,所得到的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形,这个点叫对称中心.如右图的▱ABCD是中心对称图形,两条对角线的交点是它的对称中心.
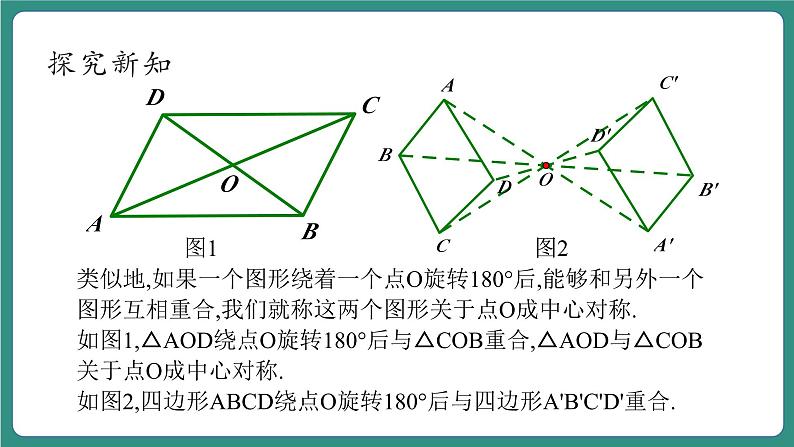
类似地,如果一个图形绕着一个点O旋转180°后,能够和另外一个图形互相重合,我们就称这两个图形关于点O成中心对称.如图1,△AOD绕点O旋转180°后与△COB重合,△AOD与△COB关于点O成中心对称.如图2,四边形ABCD绕点O旋转180°后与四边形A'B'C'D'重合.
做一做:下列哪些图形是中心对称图形?
(1)(3)(4)是中心对称图形
在▱ABCD中,已知OE=OF,找出图形中A、B、E关于点O的对称点,并说出理由.
以点E和点F为例:∵ OE=OF,又∵点E、O、F同在一条直线上,∴将点E绕着点O旋转180°后必与点F重合.∴点E与点F是关于点O的对称点同理可得A、B关于点O的对称点分别是C、D.
反过来考虑.已知点E,F关于O对称,也就是将点E绕着点O旋转180°后,要与点F重合,则点E、O、F必须同在一直线上,且OE=OF,即点O平分线段EF.
思考:你能概括出中心对称图形的性质吗?
对称中心平分连结两个对称点的线段
例1 如图,已知△ABC 和点0,作△ A'B'C' ,使△A'B'C'与△ABC关于点O成中心对称.
解:(1)连结AO并延长到A',使A'O=AO,则点A'即点A关于点O成中心对称的对称点.
(2)同理,作出点B,C的对称点B',C'.
(3)连结A'B' ,B'C' ,C'A'.△A'B'C'即为所求作的三角形.
例2 求证:在直角坐标系中,点A(x,y)与点B(-x,-y)关于原点成中心对称.
证明:如图,连结AO, BO,作AC⊥x轴,BD⊥x轴,C,D分别为垂足.∵|x|=|-x|,|y|=|-y|,∴CO= DO,AC= BD,∴Rt△AOC≌Rt△BOD.
分析:由中心对称的定义知,要证明A,B两点关于原点O对称,只需证明A,O,B三点共线,且AO=BO即可.
续:∴AO= BO,∠AOC=∠BOD.∴∠BOD+∠AOD=∠AOC+∠AOD= 180° ,即A,O,B在一条直线上,当将点A绕点0旋转180°时,点A与点B 重合. 所以点A,B关于原点成中心对称(我们也称为点A,B关于原点对称).
1.没有哪一门学科能像数学这样,利用如此多的符号图形展现一系列完备且完美的世界.下面是由4个数学式子绘制成的完美曲线,其中是中心对称图形的是( )
2.如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是( )A.点A与点A'是一对对称点B.BO=B'OC.∠AOB=∠A'OB'D.∠ACB=∠C'A'B'
3.在平面直角坐标系中,点A(-1,2)关于原点O对称的点A1的坐标是( )A.(1,2) B.(-1,-2) C.(1,-2) D.(1,0)
4.如图所示,已知线段AB和点P,求作平行四边形ABCD,使点P是它的对称中心.(不写作法,保留作图痕迹)
1.如图是厨余垃圾、可回收物、有害垃圾和其他垃圾的标识,是中心对称图形的是( )
2.下列图形中,是中心对称图形的是( )A.等腰三角形B.直角三角形C.等边三角形D.平行四边形
3.在平面直角坐标系中,点A(5,m+1)与点B(-5,-3)关于原点对称,则m的值为( )A.-4 B.4 C.2 D.-5
如图,将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,过点A作AF∥BE,交DE的延长线于点F,试问:∠B与∠F相等吗?为什么?
解: ∠B与∠F相等,理由如下:∵将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,∴∠B=∠DEC,∵AF∥BE,∴∠F=∠DEC,∴∠B=∠F.
1.什么是中心对称图形?
如果一个图形绕着一个点旋转180°后,所得到的图形能够和原来的图形互相重合,那么这个图形叫做中心对称图形
2.中心对称图形的性质是什么?
3.在直角坐标系中,点(x,y) 关于原点成中心对称的点的坐标是什么?
1.下列说法:①伸缩门的制作运用了四边形的不稳定性;②夹在两条平行线间的垂线段相等;③成中心对称的两个图形不一定是全等形;④一组对角相等的四边形是平行四边形,其中正确的有几个? ( )A.1个B.2个C.3个D.4个
2.在玩俄罗斯方块游戏时,底部已有的图形如图所示,接下来出现如下哪个形状时,通过旋转变换后能与已有图形拼成一个中心对称图形?( )
3.在平面直角坐标系中,已知点A(2a-b,-8)与点B(-2,a+3b)关于原点对称,则a、b的值为( )A.-2,-2 B.-2,2 C.2,-2 D.2,2
如图所示,四边形ABCD中,AD∥BC,点F在CD上且DF=CF,连结AF并延长交BC的延长线于E点,请证明△ADF与△ECF关于点F成中心对称.
证明:∵AD∥BC,∴∠DAF=∠CEF,又∵∠AFD=∠EFC,DF=CF,∴△ADF≌△ECF(AAS),∴AF=EF,∴△ADF与△ECF关于点F成中心对称.
数学八年级下册5.3 正方形完美版教学ppt课件: 这是一份数学八年级下册5.3 正方形完美版教学ppt课件,共30页。PPT课件主要包含了教学目标,复习导入,探究新知,课堂练习,课堂总结,作业布置,矩形的性质有什么,菱形的性质有什么,知识技能类作业,必做题等内容,欢迎下载使用。
初中数学浙教版(2024)八年级下册5.2 菱形精品教学课件ppt: 这是一份初中数学浙教版(2024)八年级下册5.2 菱形精品教学课件ppt,共30页。PPT课件主要包含了教学目标,复习导入,探究新知,课堂练习,课堂总结,作业布置,菱形的概念是什么,知识技能类作业,必做题,选做题等内容,欢迎下载使用。
初中浙教版(2024)第五章 特殊平行四边形5.2 菱形精品教学ppt课件: 这是一份初中浙教版(2024)第五章 特殊平行四边形5.2 菱形精品教学ppt课件,共30页。PPT课件主要包含了教学目标,复习导入,探究新知,课堂练习,课堂总结,作业布置,知识技能类作业,必做题,选做题,综合实践类作业等内容,欢迎下载使用。














