








所属成套资源:【新课标大单元】浙教版初数八年级下册课件+教案+大单元整体教学设计
初中数学浙教版(2024)八年级下册第五章 特殊平行四边形5.1 矩形精品教学课件ppt
展开这是一份初中数学浙教版(2024)八年级下册第五章 特殊平行四边形5.1 矩形精品教学课件ppt,共30页。PPT课件主要包含了教学目标,复习导入,探究新知,课堂练习,课堂总结,作业布置,矩形的概念是什么,知识技能类作业,必做题,选做题等内容,欢迎下载使用。
《5.1.2矩形》是“浙教版八年级数学(下)”第五章第一节第二课时的内容.本节课的主要内容是矩形的判定定理.要求学生经历矩形的判定定理的发现过程,要求学生掌握矩形的判定定理“有三个角是直角的四边形是矩形”和“对角线相等的平行四边形是矩形”,能够利用矩形的判定定理解决简单几何问题.矩形的判定定理在教材中起着承上启下的重要作用,它的学习有利于巩固和拓展学生的几何知识,可以为后续学习其它特殊四边形奠定良好的基础,是初中几何教学的重点之一.
1.经历矩形的判定定理的发现过程.2.掌握矩形的判定定理“有三个角是直角的四边形是矩形”.3.掌握矩形的判定定理“对角线相等的平行四边形是矩形”.4.感受数学证明的严谨性,提高学习数学的兴趣和信心.5.培养逻辑推理能力和发展思维能力.
有一个角是直角的平行四边形叫做矩形.
定理1:矩形的四个角都是直角.定理2:矩形的对角线相等.
矩形的性质定理是什么?
如何判断一个平行四边形是矩形?
思考:如果一个四边形,它有三个角是直角,那它是矩形吗?你能写出你的证明过程吗?
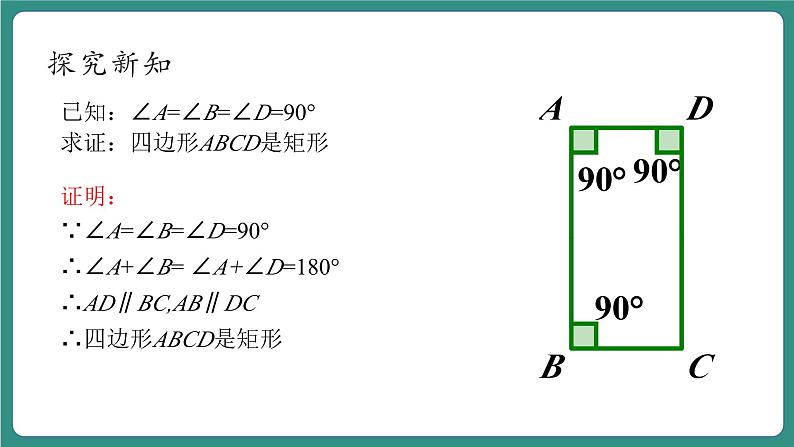
已知:∠A=∠B=∠D=90°求证:四边形ABCD是矩形
证明:∵∠A=∠B=∠D=90°∴∠A+∠B= ∠A+∠D=180°∴AD∥BC,AB∥DC∴四边形ABCD是矩形
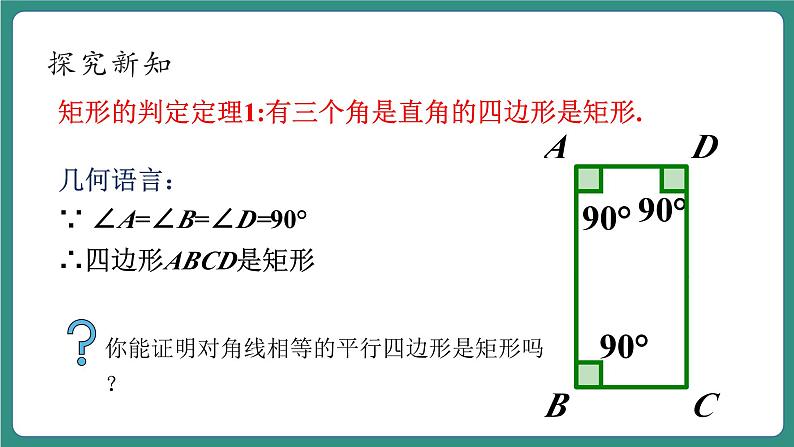
矩形的判定定理1:有三个角是直角的四边形是矩形.
几何语言:∵ ∠A=∠B=∠D=90°∴四边形ABCD是矩形
你能证明对角线相等的平行四边形是矩形吗?
已知:在▱ABCD中,AC= BD.求证: ▱ABCD是矩形
矩形的判定定理2:对角线相等的平行四边形是矩形.
几何语言:在▱ABCD中,∵ AC=BD∴ ▱ABCD是矩形
例2 如图, 一张四边形纸板ABCD的两条对角线互相垂直.若要从这张纸板中剪出一个矩形,并使它的四个顶点分别落在四边形ABCD的四条边上,可怎样剪?
解:分别取 AB, BC,CD,DA的中点E,F,G,H,依次连结EF,FG,GH,HE.沿四边形EFGH的各条边剪,就能剪出符合要求的矩形.下面给出证明.
续:∵EF是△ABC的一条中位线,∴EF//AC (三角形的中位线平行于第三边).∵AC⊥BD,∴EF⊥BD.∵EH是△ABD的一条中位线,∴EH// BD,∴EF⊥EH,即∠HEF= Rt∠.同理,∠EHG=Rt∠,∠HGF=Rt∠.∴四边形EFGH是矩形(有三个角是直角的四边形是矩形).
1.如图,要使▱ABCD成为矩形,需要添加的条件是( )A.∠A+∠B=180°B.∠B+∠C=180°C.∠A=∠B D.∠B=∠D
2.要检验一个四边形的桌面是不是矩形,可行的测量方案是( )A.测量两条对角线是否相等B.度量两个角是不是90°C.测量两条对角线的交点到四个顶点的距离是否相等D.测量两组对边是否分别相等
3.四边形ABCD的对角线AC,BD,下面给出的三个条件中,选取两个,能使四边形ABCD是矩形,①AC,BD互相平分;②AC⊥BD;③AC=BD,则正确的选法是( )①② B. ①③C. ②③ D. 以上都可以
1.如图,在四边形ABCD中,AD∥BC,AC交BD于点O,再添加什么条件可以判定四边形ABCD为矩形( )A.AB∥CD,AB=AD B.OA=OC,BC=CDC.AB=CD,AC=BD D.AD=BC,AC=BD
2.已知O为四边形ABCD对角线的交点,下列条件能使四边形ABCD成为矩形的是( )A.OA=OC,OB=OD B.AC=BDC.AC⊥BD D.∠ABC=∠BCD=∠CDA=90°
3.矩形的三个顶点坐标分别是(-2,-3),(1,-3),(-2,-4),那么第四个顶点坐标是( )A. (1,-4) B. (-8,-4)C. (1,-3) D. (3,-4)
如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.(1)求证:四边形ABCD是矩形;(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
证明:(1) ∵AO=OC,BO=OD,∴四边形ABCD是平行四边形,∵∠AOB=∠DAO+∠ADO=2∠OAD,∴∠DAO=∠ADO,∴AO=DO,∴AC=BD,∴四边形ABCD是矩形.
如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.(2)若∠AOB∶∠ODC=4∶3,求∠ADO的度数.
解:(2) ∵四边形ABCD是矩形,∴AB∥CD,∴∠ABO=∠CDO,∵∠AOB:∠ODC=4:3,∴∠AOB:∠ABO=4:3,∴∠BAO:∠AOB:∠ABO=3:4:3,∴∠ABO=54°,∵∠BAD=90°,∴∠ADO=90°-54°=36°.
矩形的判定定理2:对角线相等的平行四边形是矩形.几何语言:在▱ABCD中,∵ AC=BD∴ ▱ABCD是矩形
矩形的判定定理1:有三个角是直角的四边形是矩形.几何语言:∵ ∠DAB=∠ABC=∠BCD=90°∴四边形ABCD是矩形
2.如图,在矩形ABCD中,AB=10,P是CD边上一点,M、N、E分别是PA、PB、AB的中点,有以下四种情况,在哪一种情况下四边形PMEN不可能为矩形( )A.AD=3 B.AD=4 C.AD=5 D.AD=6
3.如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连结MN,则线段MN的长的最小值为 .
如图, ▱ABCD中,AC,BD交于点O,P是▱ABCD外一点,且∠APC=∠BPD=90°,求证: ▱ABCD是矩形.
相关课件
这是一份数学八年级下册5.3 正方形完美版教学ppt课件,共30页。PPT课件主要包含了教学目标,复习导入,探究新知,课堂练习,课堂总结,作业布置,矩形的性质有什么,菱形的性质有什么,知识技能类作业,必做题等内容,欢迎下载使用。
这是一份初中数学浙教版(2024)八年级下册第五章 特殊平行四边形5.3 正方形优秀教学课件ppt,共30页。PPT课件主要包含了教学目标,复习导入,探究新知,课堂练习,课堂总结,作业布置,两组对边分别相等,有一组邻边相等,对角线互相垂直,有一个角是直角等内容,欢迎下载使用。
这是一份初中数学浙教版(2024)八年级下册5.2 菱形精品教学课件ppt,共30页。PPT课件主要包含了教学目标,复习导入,探究新知,课堂练习,课堂总结,作业布置,菱形的概念是什么,知识技能类作业,必做题,选做题等内容,欢迎下载使用。














