

高中数学人教A版 (2019)必修 第一册2.2 基本不等式第1课时教案
展开第1课时 基本不等式
一、教学目标
1.能从实际情境中抽象归纳出算术平均数和几何平均数的概念;发现基本不等式;
2.探索基本不等式的证明过程,学生会用比较法、综合法、分析法证明基本不等式;
3.会正确地运用基本不等式解决简单的求最大值和最小值问题;
4.通过对基本不等式从感性到直观,再到理论的认识过程,体会从特殊到一般、数形结合的数学思想方法,培养数学的理性精神.
二、教学重难点
重点:掌握基本不等式的定义,几何解释.
难点:会用基本不等式求简单的最值问题.
三、教学过程
创设情境
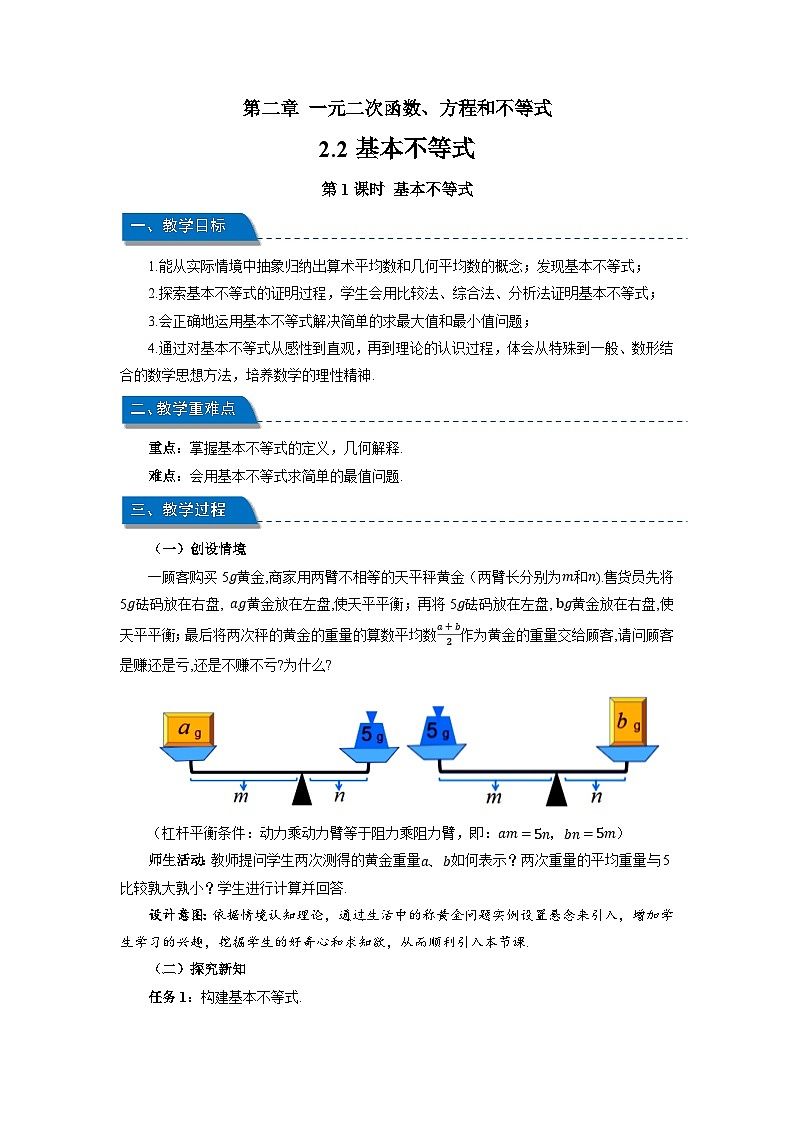
一顾客购买5g黄金,商家用两臂不相等的天平秤黄金(两臂长分别为m和n).售货员先将5g砝码放在右盘, ag黄金放在左盘,使天平平衡;再将5g砝码放在左盘, bg黄金放在右盘,使天平平衡;最后将两次秤的黄金的重量的算数平均数a+b2作为黄金的重量交给顾客,请问顾客是赚还是亏,还是不赚不亏?为什么?
(杠杆平衡条件:动力乘动力臂等于阻力乘阻力臂,即:am=5n,bn=5m)
师生活动:教师提问学生两次测得的黄金重量a、b如何表示?两次重量的平均重量与5比较孰大孰小?学生进行计算并回答.
设计意图:依据情境认知理论,通过生活中的称黄金问题实例设置悬念来引入,增加学生学习的兴趣,挖掘学生的好奇心和求知欲,从而顺利引入本节课.
(二)探究新知
任务1:构建基本不等式.
思考:阅读教材,完成下列问题
(1)什么是基本不等式,它是如何得到的?
(2)在基本不等式中,a、b的取值范围是多少?
(3)什么是算数平均数?什么是几何平均数?大小关系如何?
(4)根据以上问题,可以得到基本不等式的含义是什么?
答:(1)在重要不等式a2+b2≥2ab的基础上,如果a>0,b>0,用a代替a,用b代替b,则得到ab≤a+b2,当且仅当a=b时取等号.
(2)a>0,b>0.
(3)算数平均数:a+b2,几何平均数:ab;a+b2≥ab
(4)两个正数的算术平均数不小于几何平均数,即a+b2≥ab.
师生活动:教师提出问题,组织学生阅读材料独立思考,引导学生总结分析.教师可随机点名提问,其他学生进行补充、评价,教师可适当总结补充,并引导学生进一步理解基本不等式的构建过程.
设计意图:检查学生的变换能力,使学生了解基本不等式的形式,理解其不等号和等号成立的条件.
任务2:证明基本不等式.
思考:上面通过考察a2+b2≥2ab的特殊形式得到了基本不等式,能否直接利用不等式的性质直接推导基本不等式呢?(课件展示比较法、分析法和综合法.)
此处只展示分析法证明:
答:要证ab≤a+b2 = 1 \* GB3 ①
只要证2ab≤a+b②
要证 = 2 \∗ GB3 ②,只要证2ab−a−b≤0 = 3 \* GB3 ③
要证 = 3 \* GB3 ③,只要证−(a−b)2≤0 = 4 \* GB3 ④
要证 = 4 \* GB3 ④,只要证(a−b)2≥0 = 5 \* GB3 ⑤
显然, = 5 \* GB3 ⑤成立,当且仅当a=b时取等号,只要把上面的过程倒过来,就可以直接推出基本不等式了.
师生活动:教师引导学生体会分析法是一种“执果索因”的证明方法,即从要证明的结论出发,逐步寻求使他成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理)为止.
设计意图:根据不等式的性质,利用分析法证明基本不等式,同时引导学生认识分析法的证明过程和证明格式,为学生高中阶段的推理与证明提供更丰富的策略方法.
思考:以上方法均是从代数角度证明不等式成立,能否从几何角度进一步解释基本不等式?
任务3:基本不等式的几何解释.
探究:如图AB是圆的直径,点C是AB上一点,AC=a,BC=b,过点C做垂直于AB的弦DE,连接AD,BD.
思考:(1)线段OD,CD长为多少?
(2)如何利用这个图形得到基本不等式的几何解释?
要求:先独立思考,再合作交流.
答:(1)由图可知,OD=a+b2,又因为△ADC~△DBC,所以利用相似比可得CD=ab.
(2)根据直角三角形三边关系可知,OD>CD,当且仅当点O与点C重合时,OD=CD,综上,所以a+b2≥ab,当且仅当a=b时,等号成立.
师生活动:学生思考后回答,教师引导学生总结:从条件和基本不等式发现圆的半径长等于a+b2,CD=ab.所以基本不等式可以利用“圆中直径不小于任意一条弦”或者说“圆中半径不小于任意一条半弦”,当且仅当弦过圆心时,二者相等.
设计意图:引导学生对图形进一步分析,发现几何平均数和算术平均数的大小关系,让学生体会不仅能以数形,寻找数量关系的几何解释,还可以通过对图形的观察分析以形识数,进而完善前面的代数结论,提升逻辑推理、直观想象素养.
(三)应用举例
例1:已知x>0,求x+1x的最小值.
解:因为x>0,所以x+1x≥2x×1x=2,
当且仅当x=1x,即x2=1,x=1时,等号成立.因此所求的最小值是2.
追问1:在上述解答过程中,是否必须说明“当且仅当x=1x,x2=1,x=1时,等号成立”?
师生活动:学生讨论后回答.
教师总结:这是为了说明“2”是x=1x的一个取值.
追问2:当y0<2,x+1x≥y0,成立吗?这时能说y0是x+1xx>0的最小值吗?
师生活动:学生思考后回答.
教师总结:不能,因为x+1x的最小值,就是要求出一个y0=x0+1x0,∀x>0,x+1x≥y0,恒成立,如果y0<2找不到对应的x可以取到y0.
追问3:通过本例的解答,满足什么条件能够利用基本不等式求最小值呢?
师生活动:学生讨论后回答.根据学生实际情况,适当的引导总结:一正二定三相等.
变形:已知x<0,则x+1x有没有最值?最值是多少?
解:根据基本不等式的应用条件,原多项式可变形为x+1x=−−x+1−x,
因为x<0,所以−x>0,
所以有−x+1−x≥2−x×1−x=2,
所以−−x+1−x≤−2,
当且仅当−x=1−x,x=−1时取等号,
所以x+1x有最大值−2.
设计意图:引导学生根据所求代数式的形式,判断能否应用基本不等式解决问题,再次强调基本不等式求最值的适用范围是:一正二定三相等,同时强调代数式的最值必须是代数式能取到的值,为学生求解代数式的最值问题提供示范.
例2:已知x、y都是正数,求证:
(1)如果积xy等于定值P,那么当x=y时,和x+y有最小值2P
(2)如果x+y和等于定值S,那么当x=y时,积xy有最大值14S2
解:因为x、y都是正数,所以x+y2≥xy
当积xy等于定值P时,x+y2≥P
当且仅当x=y时,上式等号成立.于是当x=y时,和x+y有最小值2P
当x+y等于定值S时,xy≤x+y2=S2,所以xy≤14S2,
当且仅当x=y时,上式等号成立. 于是当x=y时,积xy有最大值14S2.
追问:根据上述例题可以得到什么结论?
师生活动:学生思考后回答.
教师总结:积定和最小,和定积最大.
例3:若0
所以y=x(2−x)≤x+2−x22=1,
当且仅当x=2−x时等号成立,
所以y=x(2−x)有最大值−1.
设计意图:进一步巩固求最大值的原则——和定积最大.
例4:若x>3,求函数y=x+9x−3的最值.
解:因为x>3,所以x−3>0,
所以y=x+9x−3=x−3+9x−3+3≥2x−39x−3+3=2×3+3=9,
当且仅当x−3=9x−3,即x=6时等号成立,
所以函数的最小值为9.
设计意图:让学生明确利用基本不等式求最小值要求两个正数的乘积为定值,如果不满足,不能直接使用基本不等式,可以进行配凑.
情境探究:解决开篇情境问题,请问顾客是亏还是赚?还是不亏不赚?为什么?
解:根据所学的基本不等式的知识可知,两次称重的平均重量a+b2为a、b的算术平均数,而实际重量ab为a、b的几何平均数,根据基本不等式的含义,可知a+b2≥ab, 即a+b2=125nm+5mn≥12×25nm×5mn=12×2×5=5=ab,当且仅当m=n时取等号,因为m≠n,所以a+b2>5,所以顾客赚了.
设计意图:利用刚学习的基本不等式来求解引入中的情境问题,体会整体替换的思想,灵活应用,培养学生的解题能力.
(四)课堂练习
1.若a+b=2,则3a+19⋅3b的最小值是( )
A. 1 B. 2 C. 2 3 D. 243
解:∵a+b=2,∴3a+19⋅3b≥2 3a⋅3b−2=2 3a+b−2=2×1=2,当且仅当a=0,b=2时取得“=”,所以3a+19⋅3b的最小值是2.故选B.
2.下列函数最小值为4的是( )
A. y=x+4x(x<0)B. y=x+1x−2(x>2)
C. y=x2+10 x2+6D. y=x+9x−2
解:当x=−1时,y=x+4x=−5,故排除A.
对于B,当x>2时,x−2>0,则y=x+1x−2=x−2+1x−2+2⩾2+2=4,
当且仅当x=3时,取等号,故B正确;
令y=x2+10 x2+6=4,解得x不存在,故排除C.
对于D ,当x=−1时,y=x+9x−2=−12,显然D错误.
故选B.
3.当x>1时,不等式x+1x−1≥a恒成立,则实数a的取值范围是( )
A. (−∞,3]B. [3,+∞)C. [72,+∞)D. (−∞,72]
解:令y=x+1x−1(x>1),则x−1>0,
所以y=x−1+1x−1+1⩾2 x−1·1x−1+1=2+1=3,
当且仅当x=2时,等号成立,
由题意知a≤ymin,
所以a≤3,即a的取值范围是(−∞,3].
故选:A.
4.已知函数f(x)=3−x−2x,则当x<0时,f(x)有( )
A. 最大值3+2 2B. 最小值3+2 2C. 最大值3−2 2D. 最小值3−2 2
解:由题意当x<0时,−x>0,
故f(x)=3+[(−x)+(−2x)]⩾3+2 2,等号成立当且仅当x=− 2;
又因为当x→−∞时,fx→+∞,故fx无最大值.
故选:B.
5.已知x>15,则5x+45x−1的最小值为( )
A. 4B. 5C. 6D. 7
解:因为x>15,所以5x−1>0,
所以5x+45x−1=5x−1+45x−1+1≥2 5x−1⋅45x−1+1=5,
当且仅当5x−1=45x−1,即x=35时,等号成立.
故选:B
设计意图:通过课堂练习,让学生反复巩固所学知识,能够灵活运用.
(五)归纳总结
(1)回顾本节课的内容,你都学到了什么?
研究代数性质的一般流程
设计意图:通过小结让学生进一步熟悉巩固本节课所学的知识.
必修 第一册2.2 基本不等式第2课时教学设计及反思: 这是一份必修 第一册<a href="/sx/tb_c4000263_t8/?tag_id=27" target="_blank">2.2 基本不等式第2课时教学设计及反思</a>,共8页。教案主要包含了教学目标,教学重难点,教学过程等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册2.2 基本不等式教案及反思: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4000263_t8/?tag_id=27" target="_blank">2.2 基本不等式教案及反思</a>,共8页。教案主要包含了四方面等内容,欢迎下载使用。
人教A版 (2019)必修 第一册2.2 基本不等式教案及反思: 这是一份人教A版 (2019)必修 第一册2.2 基本不等式教案及反思,共6页。教案主要包含了知识与技能,过程与方法,情感、态度与价值观,教学重点,教学难点,设计意图等内容,欢迎下载使用。













