数学必修 第一册2.2 基本不等式教学设计

基本不等式教学设计

一．学情分析

1.学生已经掌握了不等式以及一些不等关系的相关知识，特别是必修一p39页探究题，学生对于重要不等式已经有了初步了解；

2.对于基本不等式的学习,学生的认知困难主要在两个方面: (1)什么是基本不等式？学生对新概念的理解和接受是比较困难的;

(2)如何用数形结合的思路理解基本不等式？应该重视学生的独立思考和计算，重视课堂问题的讲解设计,引导学生掌握。

二．教材分析

在前面的学习中,同学们已经基本掌握了一些常见不等式及不等式证明方法,本节内容一定程度上是前面学习的运用,也是后面系统学习不等式证明的基础。基本不等式在证明不等式的过程中是一个很重要的桥梁,放缩法证明不等式会经常用到基本不等式。另一方面, 基本不等式作为求极值的的一种方法,经常运用于实际问题,而且是高考常考的知识点,通过基本不等式,常常可以将一些较为复杂的求极值的问题化为简单问题,在化归方法中起着重要的承接作用。

通过对这一节内容的学习,学生可以较为真切的体会到数形结合法的神奇之处,也加强了数学联系生活这一重要的数学观。在学习过程中,要用心体会数学思想方法,为以后抽象数学思想方法做好铺垫。

三．教学目标

1.掌握基本不等式的形式以及推导过程，会用基本不等式解决简单问题。

2,基本不等式的推导与证明过程，提升逻辑推理的思维能力。

3.基本不等式的简单应用，理解积定与和定问题。

四．教学重难点

1、重点：应用数形结合的思想理解基本不等式。

2、难点：基本不等式的推导及证明过程。

五．教学方法

情境教学、讲授法

六．教学过程

(一)创设情景，导入新课

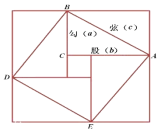
如图是在北京召开的第24届国际数学家大会的会标，会标是根据中国古代数学家赵爽的弦图设计的。三国时期吴国的数学家赵爽为《周髀算经》一书作序时，创制了一幅“勾股圆方图”，以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成。“赵爽弦图”证法的基本思想：图形经过割补后，面积不变，这就是中国古代数学中重要的面积“出入相补”原理.是我国古代数学的特色之一.
你能在这个图中找出一些相等的关系或不等关系吗？

(设计意图：通过情境导入课题，能使学生很快有新内容的学习的抵制状态，进入回忆的兴奋状态，提高学生的学习兴趣。)

(二)新课讲授

1、重要不等式

一般地，对于任意实数a, b我们有 

 a2+b2≥2ab
  当且仅当a=b时，等号成立

2、基本不等式
特别地, 若a>0, b>0, 则用√a,√b分别代替a,b,可得：
                       

当且仅当a=b时，等号成立
上述不等式称为基本不等式，其中(a+b)/2叫做正数a、b的算术平均数,√ab叫做a、b的几何平均数

3、基本不等式的证明

证明方法：作差法、综合法、分析法等

作差法：   证明：a>0, b>0   a+b/2−√ab = (√a−√b)2/2

当且仅当a=b时，等号成立

（设计意图：通过复习上一节课重要不等式的内容，利用提问法和引导法学生进行问题的探究，并进行进一步的讨论，进一步证明，理解基本不等式的定义）

(三)基本不等式的几何意义

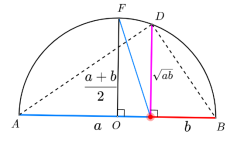如图, AB是圆O的直径，过AB上点P作垂直于AB的弦PE垂足为点D，设AD=a，BD=b，连AP，BP，
则PQ= ，
半径PO=.
几何意义：圆的半径不小于圆内半弦长
（设计意图：通过对基本不等式几何意义的进一步讲解，让学生进一步理解基本不等式）

（四）例题讲解

(1)已知x>0，求x+1/x的最小值；
(2)已知0<x<10，求x(10−x)的最大值.

解(1): x>0，则有x+1/x≥2，当且仅当x=1/x=1时取最大值。

(2)：答案25

方法总结

运用基本不等式求最值必备的三个条件：一正、二定、三相等
一正：指代a、b均为正数；
二定：指ab，a+b两者中其中一个为定值；
三相等：表示当且仅当a=b时，取等号；

（五）巩固练习

1、已知x, y都是正数，求证：
(1)x/y+y/x≥2         (2)2xy/x+y≤√xy
2、已知x, y都是正数，求证：
(1)如果积xy等于定值P，求和x+y的最小值；
(2)如果各x+y等于定值S，求积xy的最大值.
总结（和定积大、积定和小）
（1）如果x+y是定值S, 那么x=y时，积xy有 最大值1/4S2.
（2）如果xy是定值P, 那么x=y时，和x+y有最小值2√P.

七.归纳小结

1.基本不等式的形式及定义。

2,基本不等式的几何意义：圆的半径不小于圆内半弦长

3. 运用基本不等式求最值必备的三个条件：一正、二定、三相等

4.积定与和定问题。

八.作业布置

完成课后练习题第一二题。