
初中数学人教版(2024)九年级下册27.3 位似精品同步达标检测题
展开这是一份初中数学人教版(2024)九年级下册27.3 位似精品同步达标检测题,文件包含人教版数学九年级下册同步讲义练习第27章第03讲位似原卷版docx、人教版数学九年级下册同步讲义练习第27章第03讲位似解析版docx等2份试卷配套教学资源,其中试卷共50页, 欢迎下载使用。
知识点01 位似图形的概念
位似图形的概念:
如果两个图形不仅是相似图形,而且对应顶点的连线 相交于一点 ,对应边 互相平行 或在同一直线上,那么这样的两个图形叫做位似图形,这个点叫做 位似中心 。
题型考点:①位似图形的概念理解。②位似关系的判断;③确定位似中心
【即学即练1】
1.下列命题不正确的是( )
A.两个位似图形一定相似
B.位似图形的对应边若不在同一条直线上,那么一定平行
C.两个位似图形的位似比就是相似比
D.两个相似图形一定是位似图形
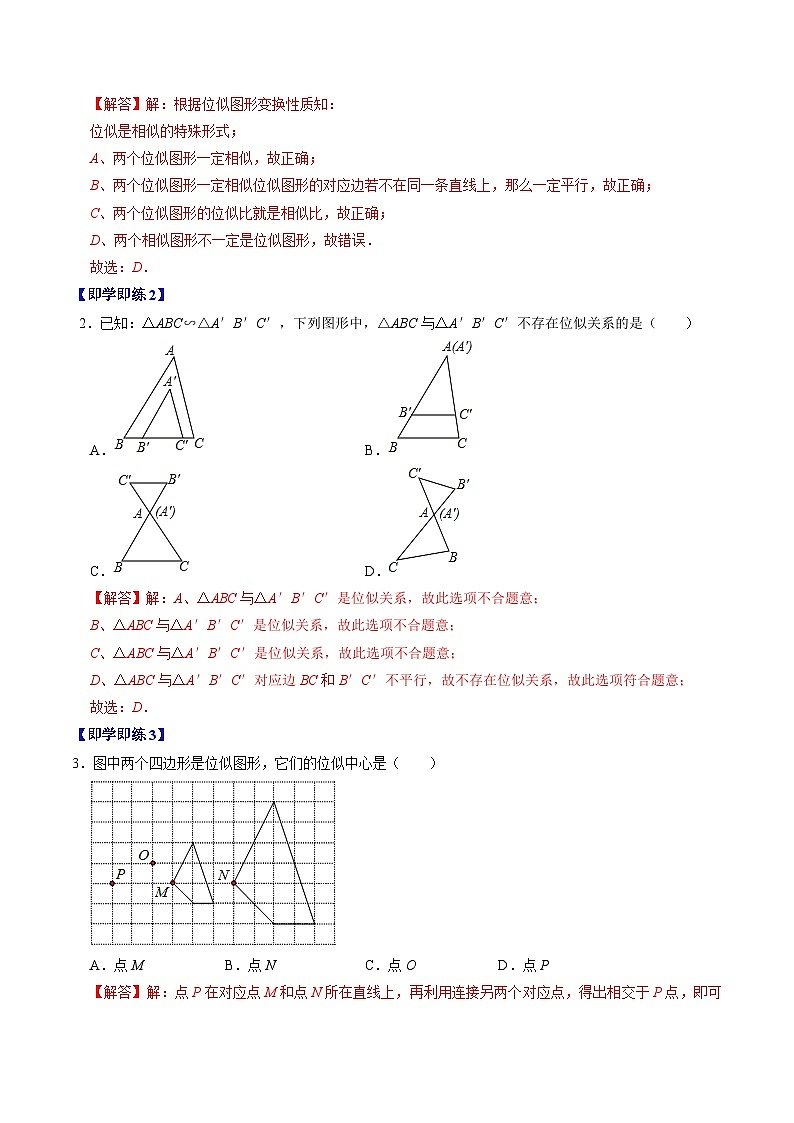
【解答】解:根据位似图形变换性质知:
位似是相似的特殊形式;
A、两个位似图形一定相似,故正确;
B、两个位似图形一定相似位似图形的对应边若不在同一条直线上,那么一定平行,故正确;
C、两个位似图形的位似比就是相似比,故正确;
D、两个相似图形不一定是位似图形,故错误.
故选:D.
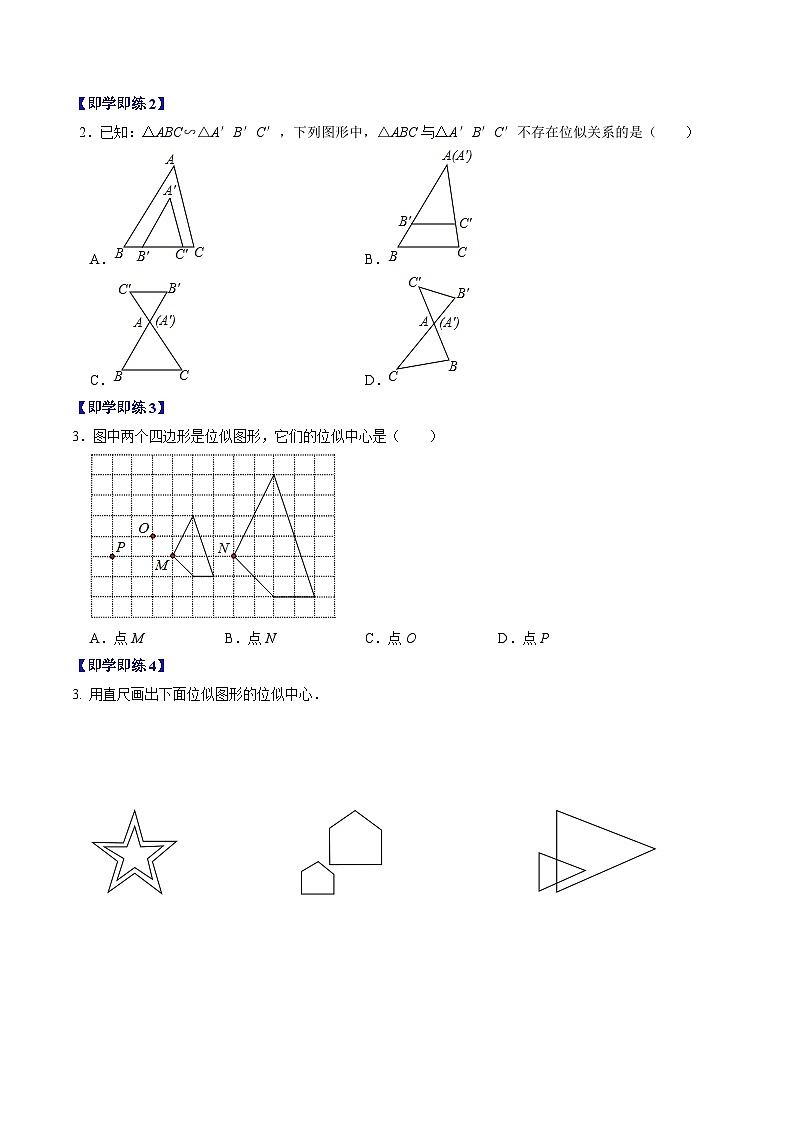
【即学即练2】
2.已知:△ABC∽△A′B′C′,下列图形中,△ABC与△A′B′C′不存在位似关系的是( )
A.B.
C.D.
【解答】解:A、△ABC与△A′B′C′是位似关系,故此选项不合题意;
B、△ABC与△A′B′C′是位似关系,故此选项不合题意;
C、△ABC与△A′B′C′是位似关系,故此选项不合题意;
D、△ABC与△A′B′C′对应边BC和B′C′不平行,故不存在位似关系,故此选项符合题意;
故选:D.
【即学即练3】
3.图中两个四边形是位似图形,它们的位似中心是( )
A.点MB.点NC.点OD.点P
【解答】解:点P在对应点M和点N所在直线上,再利用连接另两个对应点,得出相交于P点,即可得出P为两图形位似中心,
故选:D.
【即学即练4】
4.用直尺画出下面位似图形的位似中心.
【解答】解:如图,点O、P、Q分别为位似图形的位似中心.
知识点02 位似图形的性质
位似图形的性质:
①位似图形的特殊的 相似 图形,它具有 相似 图形的所有性质。
②位似图形的对应点连线交于一点,即 位似中心 。对应边 相互平行 或 在同一直线 上。
③位似图形任意一组对应点到位似中心的距离的比值等于 相似比 。
题型考点:①利用位似图形的性质求值。
【即学即练1】
5.如图,△ABC与△DEF位似,点O是位似中心,若OE=3OB,S△ABC=4,则S△DEF=( )
A.9B.12C.16D.36
【解答】解:∵△ABC与△DEF位似,
∴BC∥EF,
∴△OBC∽△OEF,
∴==,
∴=()2=,
∵S△ABC=4,
∴S△DEF=36,
故选:D.
【即学即练2】
6.如图,△ABC与△DEF位似,位似中心为点O,若OA:AD=1:2,△ABC的周长为3,则△DEF的周长为( )
A.6B.9C.12D.27
【解答】解:∵△ABC与△DEF位似,点O为位似中心.OA:AD=1:2,
∴△ABC∽△DEF,AC:DF=OA:OD=1:3,
∴△ABC的周长:△DEF的周长=1:3,
∴△DEF的周长为3×3=9.
故选:B.
【即学即练3】
7.如图,已知△ABC与△DEF位似,位似中心为点O,且OC:OF=3:2,则△ABC的周长与△DEF周长之比为( )
A.3:2B.3:5C.9:4D.9:5
【解答】解:∵△ABC与△DEF位似,位似中心为点O,
∴△ABC∽△DEF,
∴△ABC的周长与△DEF周长之比=3:2.
故选:A.
【即学即练4】
8.如图,△A′B′C和△ABC是位似三角形,位似中心为点O,OA'=2AA',则△A′B′C和△ABC的相似比为( )
A.1:4B.1:3C.4:9D.2:3
【解答】解:∵OA'=2AA',
∴OA:OA'=2:3,
∵△A′B′C和△ABC是位似三角形,
∴AC∥A′C′,
∴△AOC∽△A′OC′,
∴==,
故选:D.
知识点03 用坐标表示位似
用坐标表示位似:
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k。
即若A(x,y),以原点为位似中心,相似比为k的对应点的坐标为 。
题型考点:①求对应点的坐标。②求位似中心的坐标。
【即学即练1】
9.如图,在平面直角坐标系中的第一象限内,△ABC的顶点坐标分别是A(1,2),B(1,1),C(3,1),以原点O为位似中心,作出△ABC的位似图形△DEF.若△DEF与△ABC的相似比为2:1.则点F的坐标为( )
A.(2,4)B.(2,2)C.(6,2)D.(7,2)
【解答】解:∵△ABC与△DEF位似.△DEF与△ABC的相似比为2:1,
∴△ABC与△DEF位似比为1:2,
∵点C的坐标为(3,1),
∴点F的坐标为(3×2,1×2),即(6,2),
故选:C.
【即学即练2】
10.如图,在平面直角坐标系中,已知点A(3,4),B(6,2),以原点O为位似中心,相似比为2,把△OAB放大,则点A的对应点A'的坐标是( )
A.(6,8)B.(4,4)或(﹣4,﹣4)
C.(﹣6,﹣8)D.(6,8)或(﹣6,﹣8)
【解答】解:∵以原点O为位似中心,相似比为2,把△OAB放大,点A的坐标为(3,4),
∴点A的对应点A'的坐标为(3×2,4×2)或(3×(﹣2),4×(﹣2)),即(6,8)或(﹣6,﹣8),
故选:D.
【即学即练3】
11.如图所示,在平面直角坐标系中,已知点O(0,0),A(8,0),B(0,6),以某点为位似中心,作出△AOB的位似图形△CED,则位似中心的坐标为( )
A.(0,0)B.(1,1)C.(2,2)D.(0,6)
【解答】解:延长OE、AC交于点P,
∵△AOB和△CED是位似图形,
∴点P为位似中心,
由图可知,点P的坐标为(2,2),
故选:C.
【即学即练4】
12.如图,在平面直角坐标系中,△AOB与△COD是以点O为位似中心的位似图形,若A(3,0),B(2,﹣1),C(6,0),则点B的对应点D的坐标为( )
A.(4,﹣2)B.(6,﹣3)C.(4,2)D.(6,3)
【解答】解:∵△AOB与△COD是以点O为位似中心的位似图形,相似比为1:2,
∴点B的坐标为(2×2,﹣1×2),即(4,﹣2),
故选:A.
知识点04 位似作图
位似作图:
利用位似,可以将一个图形 放大 或 缩小 ,画位似图形的一般步骤为:
①确定 位似中心 和 图形关键点 。分别作他们所在的直线。
②根据 位似比 ,确定能代表所作的位似图形的关键点。
③顺次连接上述各点,得到放大或缩小的图形。
题型考点:①进行位似作图。
【即学即练1】
13.如图所示,在平面直角坐标系中,有两点A(4,2),B(3,0),以原点为位似中心,A′B′与AB的相似比为,得到线段A′B′.正确的画法是( )
A.B.
C.D.
【解答】解:画出图形,如图所示:
故选:D.
【即学即练2】
14.如图,△ABC三个顶点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).在平面直角坐标系中,以原点O为位似中心,将△ABC放大为原来的2倍得到的图形画出来.
【解答】解:如图,△A'B'C'与△A''B''C''均满足题意.
【即学即练3】
15.在平面直角坐标系内,△ABC的位置如图所示.
(1)画出与△ABC关于y轴对称的△A1B1C1.
(2)以原点O为位似中心,在第四象限内作出△ABC的位似图形△A2B2C2,且△A2B2C2与△ABC的相似比为2:1.
【解答】解:(1)如图,△A1B1C1即为所作.
(2)如图,△A2B2C2即为所作.
【即学即练4】
16.在正方形网格中,每个小正方形的边长为1,△ABC在平面直角坐标系中的位置如图所示.
(1)以原点O为位似中心,在网格中y轴右侧作出△ABC的位似图形△A1B1C1,使△ABC与△A1B1C1的相似比为1:2;
(2)作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C即为所求.
题型01 利用位似的性质求值
【典例1】
如图,△ABC和△DEF是以点O为位似中心的位似图形.若OA:AD=2:3,则△ABC与△DEF的周长比是( )
A.2:3B.4:9C.2:5D.4:25
【解答】解:∵△ABC和△DEF是以点O为位似中心的位似图形.
∴△ABC和△DEF的位似比为OA:OD,
∵OA:AD=2:3,
∴OA:OD=2:5,
∴△ABC与△DEF的周长比是2:5.
故选:C.
【典例2】
如图,△ABC与△DEF关于点O位似,且相似比为3:4,则AB与DE的比为( )
A.3:4B.2:7C.9:16D.4:3
【解答】解:∵△ABC与△DEF关于点O位似,
∴△ABC∽△DEF,
∵△ABC与△DEF的相似比为3:4,
∴AB与DE的比为3:4,
故选:A.
【典例3】
如图,已知△ABC与△DEF位似,位似中心为O,且△ABC与△DEF的周长之比是4:3,则AO:DO的值为( )
A.4:7B.4:3C.3:4D.16:9
【解答】解:∵△ABC与△DEF位似,
∴△ABC∽△DEF,AB∥DE,
∵△ABC与△DEF的周长之比是4:3,
∴AB:DE=4:3,
∵AB∥DE,
∴△AOB∽△DOE,
∴AO:DO=AB:DE=4:3,
故选:B.
【典例4】
如图,四边形ABCD和A'B'C'D'是以点O为位似中心的位似图形,若OB:OB'=1:2,则四边形ABCD与A'B'C'D'的周长比是( )
A.1:2B.1:4C.1:D.1:3
【解答】解:∵四边形ABCD和四边形A'B'C'D'是以点O为位似中心的位似图形,OB:OB'=1:2,
∴四边形ABCD和四边形A'B'C'D'的相似比为1:2,
∴四边形ABCD与四边形A'B'C'D'的周长比为1:2.
故选:A.
【典例5】
如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(﹣2,0),D(3,0),且AC=,则线段DF的长度为( )
A.B.C.D.
【解答】解:∵△ABC与△DEF是以坐标原点O为位似中心的位似图形,A(﹣2,0),D(3,0),
∴△ABC∽△DEF,且相似比为2:3,
∴=,
∵AC=2,
∴DF=3,
故选:B.
题型02 坐标表示位似
【典例1】
如图,在直角坐标系中,△ABC与△ODE是位似图形,已知点A(2,1),则位似中心的坐标是( )
A.(1,5)B.(4,2)C.(1,4)D.(5,2)
【解答】解:连接DB,OA并延长,交于点M,点M即为位似中心,如图,
∴M点坐标为(4,2),
故答案为:B.
【典例2】
如图,将视力表中的两个“E”放在平面直角坐标系中,两个“E”字是位似图形,位似中心点O,①号“E”与②号“E”的相似比为2:1.点P与Q为一组对应点,若点Q坐标为(﹣2,3),则点P的坐标为( )
A.B.(﹣6,4)C.D.(﹣4,6)
【解答】解:∵①号“E”与②号“E”的相似比为2:1,点Q坐标为(﹣2,3)
∴点P的坐标为(﹣2×2,3×2),即(﹣4,6),
故选:D.
【典例3】
如图,若△ABC与△A1B1C1是位似图形,则位似中心的坐标为( )
A.(0,0)B.(0,1)C.(﹣1,0)D.(0,﹣1)
【解答】解:如图所示:位似中心的坐标为(0,﹣1).
故选:D.
【典例4】
在平面直角坐标系中,已知点A(﹣4,2),B(﹣6,﹣4),以原点O为位似中心,相似比为2,把△ABO放大,则点B的对应点B'的坐标是( )
A.(﹣3,﹣2)B.(﹣3,﹣2)或(3,2)
C.(﹣12,﹣8)D.(﹣12,﹣8)或(12,8)
【解答】解:∵以原点O为位似中心,相似比为2,把△ABO放大,B(﹣6,﹣4),
点B'的对应点A'的坐标为(﹣6×2,﹣4×2)或(﹣6×(﹣2),﹣4×(﹣2)),即点B'的坐标为(﹣12,﹣8)或(12,8),
故选:D.
【典例5】
如图,在平面直角坐标系中,△AOB的顶点A的坐标为(﹣2,4).若以原点O为位似中心,相似比为,把△AOB缩小,则点A的对应点A′的坐标是( )
A.B.或
C.(﹣8,16)D.(﹣8,16)或(8,﹣16)
【解答】解:∵以原点O为位似中心,相似比为,把△AOB缩小,点A的坐标为(﹣2,4),
∴点A的对应点A′的坐标为(﹣2×,4×)或(﹣2×(﹣),4×(﹣)),即(﹣,1)或(,﹣1),
故选:B.
题型03 位似规律题
【典例1】
如图,在平面直角坐标系中,点A的坐标为(2,1),点B的坐标为(1,2),以点O为位似中心,在点O的异侧作△OAB的位似图形△OA1B1,使△OAB与△OA1B1的相似比为1:2;再以点O为位似中心,在点O的异侧作△OA1B1的位似图形△OA2B2,使△OA1B1与△OA2B2的相似比为1:2⋯⋯以此类推,则点B2023的坐标为 (﹣22023,﹣22024) .
【解答】解:根据题意,点B的坐标为(1,2),在点O的异侧作△OAB的位似图形△OA1B1,使△OAB与△OA1B1的相似比为1:2,
则B1(﹣2,﹣4),
再以点O为位似中心,在点O的异侧作△OA1B1的位似图形△OA2B2,使△OA1B1与△OA2B2的相似比为1:2,
则B2(4,8),
……
所以,点,
故点B2023的坐标为(﹣22023,﹣22024).
故答案为:(﹣22023,﹣22024).
【典例2】
如图,在平面直角坐标系中,矩形AOCB的两边OA,OC分别在x轴和y轴上,且OA=2.OC=1,则矩形AOCB的对称中心的坐标是 (﹣1,) ;在第二象限内,将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,再将矩形A1OC1B1以原点O为位似中心放大倍,得到矩形A2OC2B2,…,按此规律,则矩形A4OC4B4的对称中心的坐标是 (﹣,) .
【解答】解:∵OA=2.OC=1,
∴B(﹣2,1),
∴矩形AOCB的对称中心的坐标为(﹣1,),
∵将矩形AOCB以原点O为位似中心放大为原来的倍,得到矩形A1OC1B1,
∴B1(﹣3,),
同理可得B2(﹣,),B3(﹣,),B4(﹣,),
∴矩形A4OC4B4的对称中心的坐标是 (﹣,).
故答案为 (﹣1,),(﹣,).
题型04 位似作图
【典例1】
如图,点P(﹣6,6)和△ABC在平面直角坐标系中,点A的坐标是(4,4).
(1)画出△ABC关于y轴对称的图形△A'B'C';
(2)以点P为位似中心作△DEF,使△DEF与△A'B'C'位似,且这两个三角形在点P的同侧,相似比为2,并写出点A'的对应点D的坐标.
【解答】解:(1)如图,△A'B'C'即为所求.
(2)如图,△DEF即为所求.
点D的坐标为(﹣2,2).
【典例2】
如图,△ABC在平面直角坐标系内三顶点的坐标分别为A(﹣1,2),B(﹣3,3),C(﹣3,1).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)以B为位似中心,在B的下方画出△A2BC2,使△A2BC2与△ABC位似且相似比为2:1;
(3)直接写出点A2和点C2的坐标.
【解答】解:(1)如图1所示,△A1B1C1即为所求;
(2)如图所示,△A2BC2即为所求;
(3)依据图2可知,A2(1,1),C2(﹣3,﹣1).
【典例3】
如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(2,1),B(1,﹣2).
(1)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA1B1,使它与△OAB的位似比为2:1;
(2)画出将△OAB向左平移2个单位,再向上平移1个单位后得到的△O2A2B2;
(3)判断△OA1B1和△O2A2B2是位似图形吗?若是,请在图中标出位似中心点M,并写出点M的坐标.
【解答】解:(1)如图,△OA1B1即为所作图形;
(2)如图,△O2A2B2即为所作图形;
(3)△OA1B1和△OA2B2是位似图形,点M为所求位似中心,点M的坐标为(﹣4,2).
【典例4】
如图,已知O是坐标原点,A、B的坐标分别为(3,1)、(2,﹣1).
(1)画出△OAB绕点O顺时针旋转180°后得到的图形.
(2)在y轴的左侧以O为位似中心作△OAB的位似三角形OCD,使新图与原图的相似比为2:1,并分别写出A、B的对应点C、D的坐标.
【解答】解:(1)如图所示,△OA′B′即为所求;
(2)如图所示△OCD即为所求,D(﹣4,2),C(﹣6,﹣2).
1.若两个直角三角形都有一个30°的内角,则这两个直角三角形一定( )
A.全等B.相似C.位似D.无法确定
【解答】解:如果两个直角三角形都有一个30°的内角,那么这两个三角形有两角对应相等,
所以这两个三角形相似,
因为没有给出对应边的关系,所以两个三角形不一定全等,
故选:B.
2.如图,在正方形网格中,以点O为位似中心,△ABC的位似图形可以是( )
A.△DEFB.△DHFC.△GEHD.△GDH
【解答】解:∵△ABC与△GEH是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,
∴△ABC与△GEH是位似图形,
故选:C.
3.如图所示△DEF是△ABC位似图形的几种画法,其中正确的个数是( )
A.4B.3C.2D.1
【解答】解:第一个图形中的位似中心为A点,第二个图形中的位似中心为AD与BC的交点,第三个图形中的位似中心为O点,第四个图形中的位似中心为O点.
故选:A.
4.如图,以点O为位似中心,将△OAB放大后得到△OCD,OA=3,AC=5,则=( )
A.B.C.D.
【解答】解:∵以点O为位似中心,将△OAB放大后得到△OCD,
∴△OAB∽△OCD,
∴.
故选:A.
5.如图,△ABC和△DEF是以点O为位似中心的位似图形,相似比为2:3,则△DEF和△ABC的面积比是( )
A.4:9B.9:4C.2:3D.3:2
【解答】解:∵△ABC和△DEF是以点O为位似中心的位似图形,
∴△ABC∽△DEF,
∵△ABC和△DEF的相似比为2:3,
∴△DEF与△ABC和的相似比为3:2,
∴△DEF和△ABC的面积比为9:4,
故选:B.
6.如图,△ABC与△DEF位似,点O为位似中心,位似比为1:2,BC=2,则EF的长度为( )
A.3B.4C.6D.8
【解答】解:∵△ABC与△DEF位似,点O为位似中心,位似比为1:2,
∴△ABC∽△DEF,相似比为1:2,
∴BC:EF=1:2,
即2:EF=1:2,
解得EF=4,
即EF的长度为4.
故选:B.
7.如图,点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,若OA:OA1=3:4,则五边形ABCDE和五边形A1B1C1D1E1的面积比是( )
A.2:3B.3:4C.3:7D.9:16
【解答】解:∵五边形ABCDE和五边形A1B1C1D1E1是位似图形,
∴AB∥A1B1,
∴△OAB∽△OA1B1,
∴==,
∴五边形ABCDE和五边形A1B1C1D1E1的面积比为:()2=,
故选:D.
8.如图,矩形EFGO的两边在坐标轴上,点O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(﹣4,4),(2,1),则位似中心的坐标为( )
A.(0,3)B.(0,2.5)C.(0,2)D.(0,1.5)
【解答】解:如图,连接BF交y轴于P,
∵四边形ABCD和四边形EFGO是矩形,点B,F的坐标分别为(﹣4,4),(2,1),
∴点C的坐标为(0,4),点G的坐标为(0,1),
∴CG=3,
∵BC∥GF,
∴==,
∴GP=1,PC=2,
∴点P的坐标为(0,2),
故选:C.
9.如图,△ABC和△A'B'C'是以点O为位似中心的位似图形,点A在线段OA′上.若OA:AA′=1:2,则△ABC与△A'B'C'的周长之比为 1:3 .
【解答】解:∵OA:AA′=1:2,
∴OA:OA′=1:3,
∵△ABC和△A′B′C′是以点O为位似中心的位似图形,
∴AC∥A′C′,△ABC∽△A′B′C′,
∴△AOC∽△A′OC′,
∴AC:A′C′=OA:OA′=1:3,
∴△ABC与△A′B′C′的周长比为1:3,
故答案为:1:3.
10.在平面直角坐标系中,已知点A(﹣3,6)、B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,则点B对应点B'的坐标是 (﹣3,﹣1)或(3,1) .
【解答】解:∵点A(﹣3,6)、B(﹣9,﹣3),以原点O为位似中心,相似比为,把△ABO缩小,
∴点B的对应点B′的坐标是:(﹣9×,﹣3×)或[﹣9×(﹣),﹣3×(﹣)],即(﹣3,﹣1)或(3,1).
故答案为:(﹣3,﹣1)或(3,1).
11.在平面直角坐标系中,已知点A(﹣4,2),B(﹣6,﹣4),以原点O为位似中心,画△A′B′O,使它与△ABO位似,且相似比为1:2,则点B的对应点B′的坐标是 (﹣3,﹣2)或(3,2) .
【解答】解:∵△A′B′O与△ABO位似,以原点O为位似中心,且相似比为1:2,B(﹣6,﹣4),
∴点B的对应点B′的坐标是(﹣6×,﹣4×)或(﹣6×(﹣),﹣4×(﹣)),即(﹣3,﹣2)或(3,2),
故答案为:(﹣3,﹣2)或(3,2).
12.如图,在直角坐标系中,每个网格小正方形的边长均为1个单位长度,以点P为位似中心作正方形PA1A2A3,正方形PA4A5A6,…,按此规律作下去,所作正方形的顶点均在格点上,其中正方形PA1A2A3的顶点坐标分别为P(﹣3,0),A1(﹣2,1),A2(﹣1,0),A3(﹣2,﹣1),则顶点A2023的坐标为 (672,675) .
【解答】解:∵A1(﹣2,1),A4(﹣1,2),A7(0,3),A10(1,4),…,
∴A3n﹣2(n﹣3,n),
∵2023=3×675﹣2,
∴A2023的坐标为(672,675),
故答案为:(672,675).
13.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣2,4),B(4,4),C(6,0).
(1)请以原点O为位似中心,画出△A′B′C′,使它与△ABC的相似比为1:2,变换后点A、B的对应点分别为点A′、B′,点B′在第一象限;
(2)若P(a,b)为线段BC上的任一点,则变换后点P的对应点P′的坐标为 (,) .
【解答】解:(1)如图所示:△A'B'C'即为所求;
(2)若P(a,b)为线段BC上的任一点,则变换后点P的对应点P'的坐标为:(,).
故答案为:(,).
14.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,﹣2),B(2,﹣1),C(4,﹣3).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以点O为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比为2:1;
(3)设点P(a,b)为△ABC内一点,则依上述两次变换后点P在△A2B2C2内的对应点P2的坐标是 (2a,﹣2b) .
【解答】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)点P的对应点P2的坐标是(2a,﹣2b).
故答案为(2a,﹣2b).
15.如图,每一个小方格的边长均为一个单位长度,△ABC的顶点的坐标分别为A(﹣2,﹣2),B(﹣5,﹣4)C(﹣1,﹣5).
(1)请在网格中画出△ABC关于y轴对称的图形△A1B1C1;
(2)以点O为位似中心,把△ABC按2:1放大,在y轴右侧得△A2B2C2,请在网格中画出△A2B2C2;
(3)求经过点C与A2的一次函数解析式.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)设经过点C与A2的一次函数解析式为y=kx+b,
将C(﹣1,﹣5),A2(4,4)代入,
得,
解得,
∴经过点C与A2的一次函数解析式为y=.
课程标准
学习目标
①位似的定义与性质
②平面直角坐标系中的位似
掌握位似图形的概念与位似图形的性质,并且能够熟练的应用其性质解决相关题目。
掌握平面直角坐标系中的位似,能够利用位似的性质进行求解坐标与作图等。
相关试卷
这是一份人教版(2024)七年级下册7.2.2用坐标表示平移当堂达标检测题,文件包含人教版数学七年级下册同步讲义+练习第七章第03讲坐标方法的简单应用2个知识点+5类热点题型讲练+习题巩固原卷版docx、人教版数学七年级下册同步讲义+练习第七章第03讲坐标方法的简单应用2个知识点+5类热点题型讲练+习题巩固解析版docx等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。
这是一份初中数学人教版(2024)七年级下册6.3 实数优秀课堂检测,文件包含人教版数学七年级下册同步讲义+练习第六章第03讲实数6个知识点+7类热点题型讲练+习题巩固原卷版docx、人教版数学七年级下册同步讲义+练习第六章第03讲实数6个知识点+7类热点题型讲练+习题巩固解析版docx等2份试卷配套教学资源,其中试卷共36页, 欢迎下载使用。
这是一份人教版(2024)七年级上册1.2.3 相反数精品课堂检测,文件包含人教版数学七年级上册同步讲义+练习第一章第03讲相反数原卷版docx、人教版数学七年级上册同步讲义+练习第一章第03讲相反数解析版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。













