

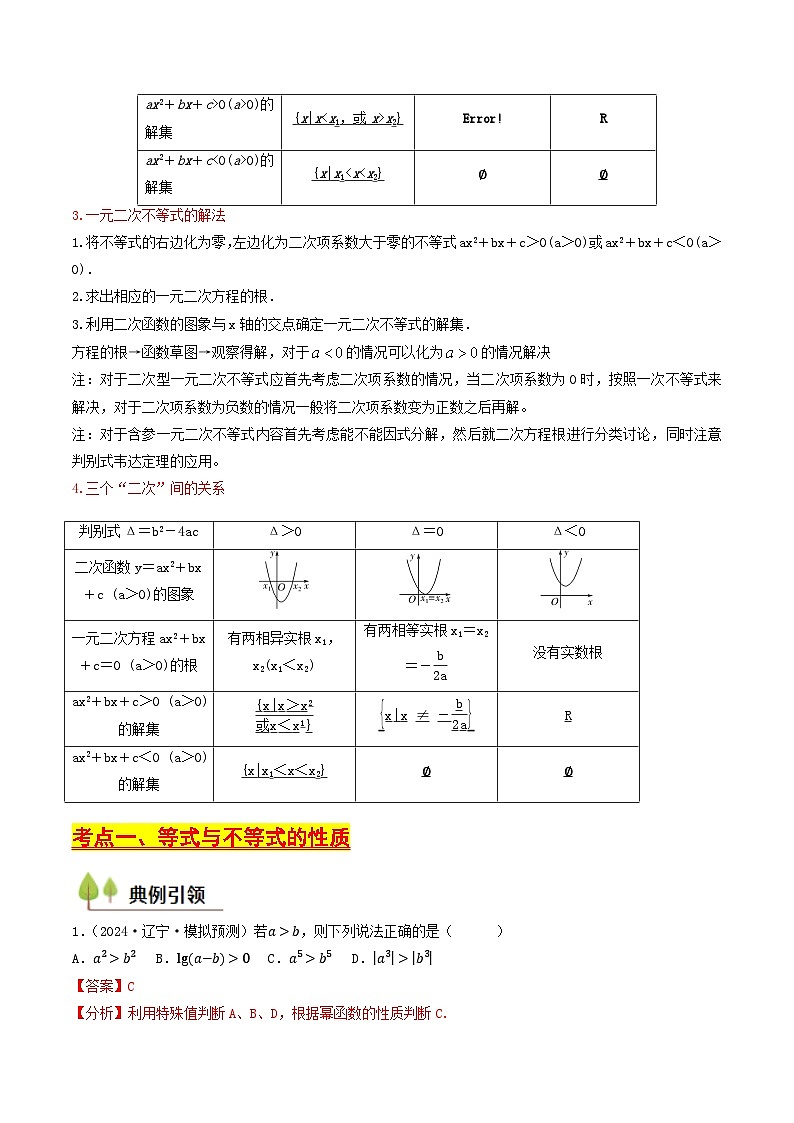


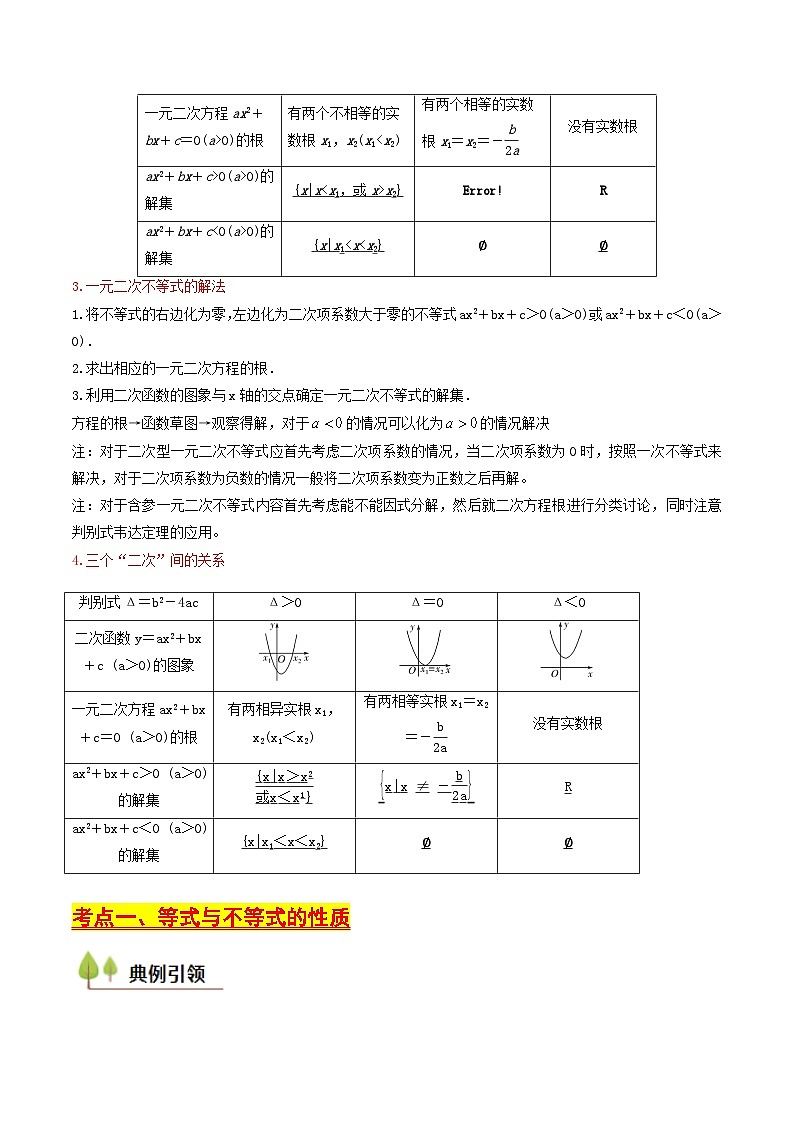
第02讲 等式与不等式(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案
展开第01讲 集合与常用逻辑用语(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案: 这是一份第01讲 集合与常用逻辑用语(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案,文件包含第01讲集合与常用逻辑用语教师版备战2025年高考数学一轮复习考点帮天津专用docx、第01讲集合与常用逻辑用语学生版备战2025年高考数学一轮复习考点帮天津专用docx等2份学案配套教学资源,其中学案共43页, 欢迎下载使用。
高考数学一轮复习第6章不等式第4讲基本不等式学案: 这是一份高考数学一轮复习第6章不等式第4讲基本不等式学案,共10页。
高考数学一轮复习第6章不等式第1讲不等关系与不等式学案: 这是一份高考数学一轮复习第6章不等式第1讲不等关系与不等式学案,共8页。












