

所属成套资源:备战2025年高考数学一轮复习考点帮(天津专用)
第01讲 集合与常用逻辑用语(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案
展开这是一份第01讲 集合与常用逻辑用语(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案,文件包含第01讲集合与常用逻辑用语教师版备战2025年高考数学一轮复习考点帮天津专用docx、第01讲集合与常用逻辑用语学生版备战2025年高考数学一轮复习考点帮天津专用docx等2份学案配套教学资源,其中学案共43页, 欢迎下载使用。
1. 5年真题考点分布
2. 命题规律及备考策略
【命题规律】本节内容是天津高考卷的必考内容,设题稳定,难度较低,分值为5分
【备考策略】1.理解、掌握集合的表示方法,充分条件与必要条件的判断,能够判断元素与集合、集合与集合的关系,能够判断命题的充分条件与必要条件
2.能掌握集合交集、并集、补集的运算和性质,会判断充分条件与必要条件
3.具备数形结合的思想意识,会借助Venn图、数轴等工具解决集合的计算问题,会利用集合间的关系解决充分条件必要条件问题
【命题预测】本节内容是天津高考卷的必考内容,一般给两个集合,要求通过解不等式求出一个集合,然后通过集合的运算得出答案,一般给出两命题,要求判断两个命题的充分条件与必要条件等。
知识讲解
知识点一.集合的含义与表示
1.集合的概念
集合中的元素具有确定性、互异性和无序性
2.常用数集及其记法
N表示自然数集,N*或N,表示正整数集,Z表示整数集,0表示有理数集,R表示实数集
3.集合与元素间的关系
对象a与集合M的关系是a ∈M,或者a ¢M,两者必居其一。
4.集合的表示法
①自然语言法:用文字叙述的形式来描述集合
②)列举法:把集合中的元素--列举出来,写在大括号内表示集合
③描述法:{xlx具有的性质},其中x为集合的代表元素、
④图示法:用数轴或韦恩图来表示集合
5.集合的分类
①含有有限个元素的集合叫做有限集
②含有无限个元素的集合叫做无限集
③不含有任何元素的集合叫做空集(Ø)
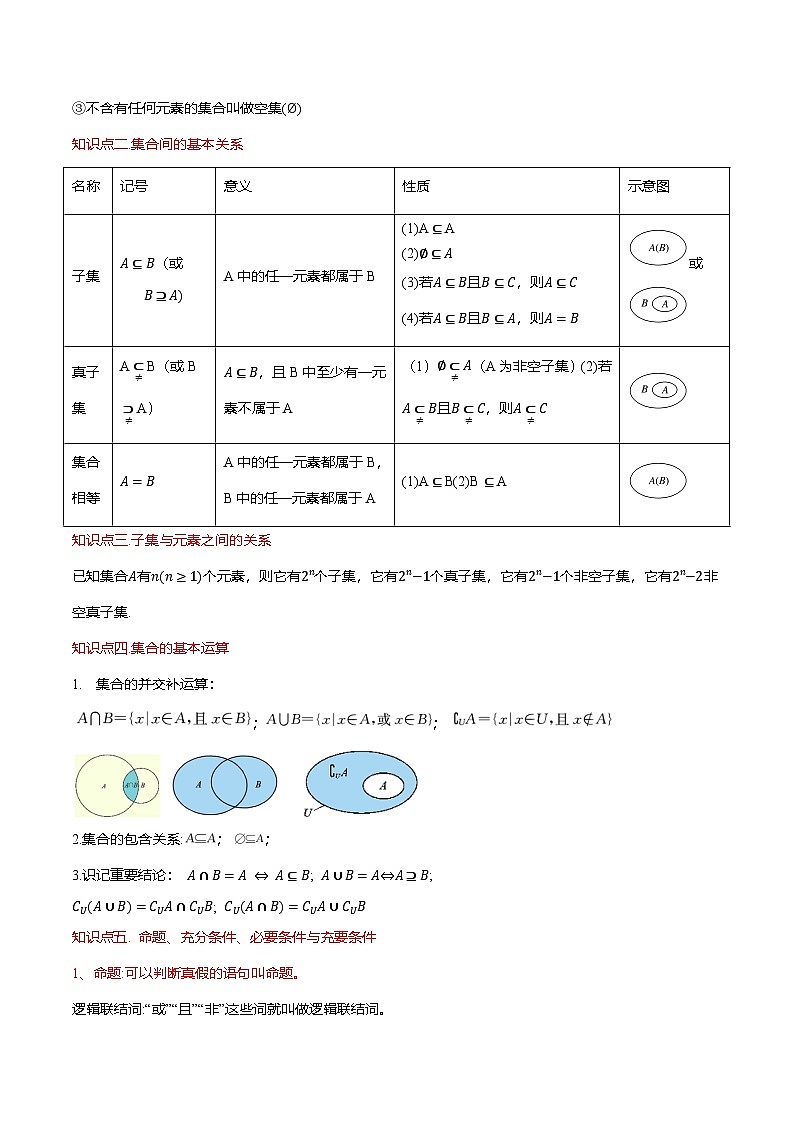
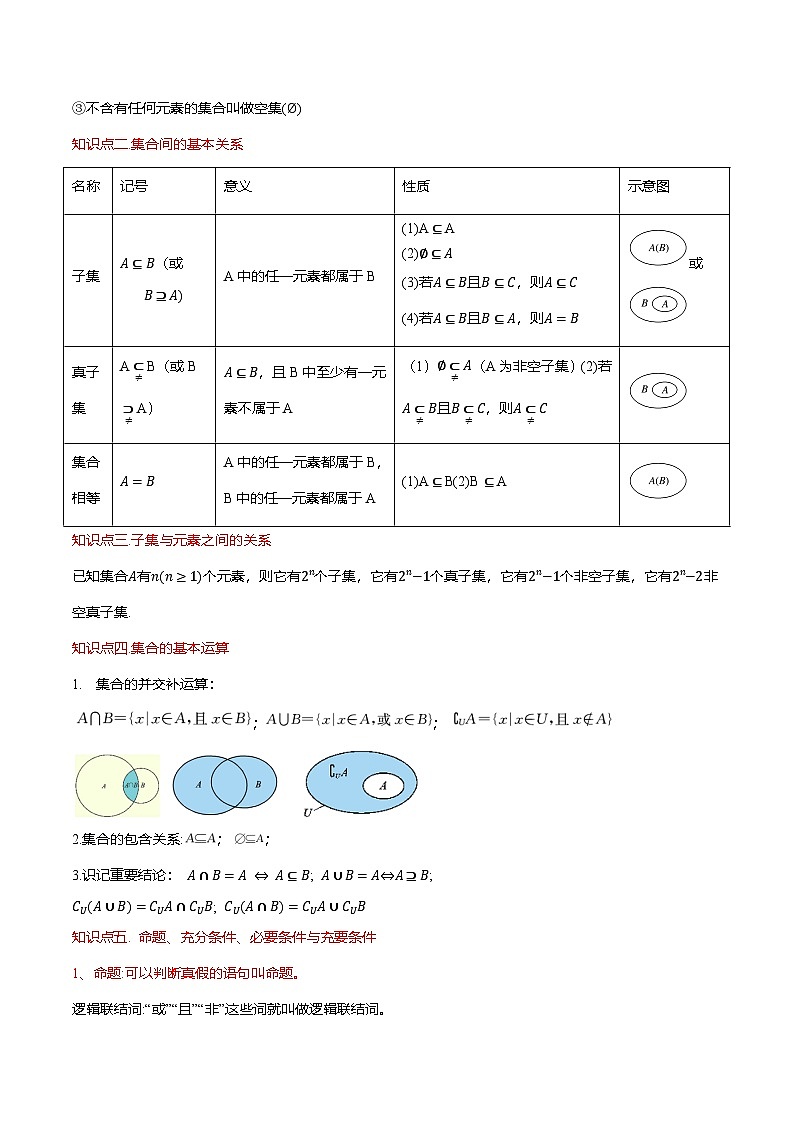
知识点二.集合间的基本关系
知识点三.子集与元素之间的关系
已知集合A有n(n≥1)个元素,则它有2n个子集,它有2n−1个真子集,它有2n−1个非空子集,它有2n−2非空真子集.
知识点四.集合的基本运算
集合的并交补运算:
;;
2.集合的包含关系:;;
3.识记重要结论: A∩B=A ⇔ A⊆B; A∪B=A⇔A⊇B;
CUA∪B=CUA∩CUB; CUA∩B=CUA∪CUB
知识点五. 命题、充分条件、必要条件与充要条件
1、命题:可以判断真假的语句叫命题。
逻辑联结词:“或”“且”“非”这些词就叫做逻辑联结词。
简单命题:不含逻辑联结词的命题。
复合命题:由简单命题与逻辑联结词构成的命题常用小写的拉丁字母p,q,r,s,.表示命题
2、充分条件、必要条件与充要条件
(1)、一般地,如果已知p⟹q,那么就说:p是q的充分条件,q是p的必要条件;
若p ⟺q,则p是q的充分必要条件,简称充要条件
(2)、充分条件,必要条件与充要条件主要用来区分命题的条件p与结论g之间的关系
3、从逻辑推理关系上看:
①若p⟹q,则p是q充分条件,q是p的必要条件;
②若p⟹q,但q⇏p,则p是q充分而不必要条件:
③若p⇏q,但q⟹p,则p是q必要而不充分条件;
④若p⟹q且q ⟹p,则p是q的充要条件;
⑤若p⇏q且q⇏p,则p是q的既不充分也不必要条件,
4、从集合与集合之间的关系上看:
已知A ={x|x满足条件p},B = {x|x满足条件q}
①A ⊆B,则p是q充分条件;
②若B⊆A,则p是q必要条件;
③若A ⊂≠B,则p是q充分而不必要条件;
④若B ⊂≠A,则p是q必要而不充分条件;
⑤若A =B,则p是q的充要条件;
⑥若A ¢ B且B ¢A,则p是q的既不充分也不必要条件
5、全称量词与存在量词
(1)全称量词与全称命题
短语“所有的”“任意一个”在逻辑中通常叫做全称量词,并用符号“∀”表示.含有全称量词的命题,叫做全称命题
(2)存在量词与特称命题
短语“存在一个”“至少有一个”在逻辑中通常叫做存在量词,并用符号“∃”表示.含有存在量词的命题,叫做特称命题
(3)全称命题与特称命题的符号表示及否定
①全称命题p: ∀x ∈ M,p(x),它的否定¬p: ∃x∈ M, ¬p(x).全称命题的否定是特称命题
②特称命题p: ∃ x ∈ M,p(x),它的否定¬p: ∀x ∈ M, ¬p(x).特称命题的否定是全称命题
考点一、元素与集合的关系
1.(2022·全国·高考真题)设全集U={1,2,3,4,5},集合M满足∁UM={1,3},则( )
A.2∈MB.3∈MC.4∉MD.5∉M
2.(2024·四川·模拟预测)已知全集U=−2,−1,0,1,2,A∩B=−1,1,A∪B=−2,−1,1,2,则( )
A.−1∈A,−1∉BB.2∈A,2∈B
C.−2∉A,−2∉BD.0∉A,0∉B
1.(2023·黑龙江哈尔滨·模拟预测)已知A=xmx+1mx−1≤0,若2∈A,则m的取值范围是( )
A.−12≤m<12B.−12≤m≤12C.m≤−12或m>12D.m≤−12或m≥12
2.(2024·河南信阳·模拟预测)已知非空集合A=xa
C.−∞,0∪1,+∞D.−∞,−1∪0,+∞
3.(2024·北京·三模)已知集合A=xlnx<1,若a∉A,则a可能是( )
A.1eB.1C.2D.3
4.(2023·北京房山·二模)设集合A={(x,y)|x−y≥0,ax+y≥2,x−ay≤2},则( )
A.当a=1 时,(1,1)∉AB.对任意实数a,(1,1)∈A
C.当a<0时,(1,1)∉AD.对任意实数a,(1,1)∉A
5.(23-24高三上·北京海淀·阶段练习)已知集合A={x∣x>aa−1},0∈A,则a的取值范围是 .
6.(23-24高三上·上海普陀·期末)已知0∈2,x2−1,则实数x= .
考点二、集合中元素的特征
1.(2023·全国·高考真题)已知等差数列an的公差为2π3,集合S=csann∈N∗,若S=a,b,则ab=( )
A.-1B.−12C.0D.12
2.(23-24高三上·辽宁丹东·期中)已知集合A=0,1,a2,B=1,0,2a+3,若A=B,则a=( )
A.−1或3B.0C.3D.−3
1.(2024·江苏连云港·模拟预测)已知集合A=1,3,a2,集合B=1,2+a,若A∪B=A,则a= .
2.(23-24高三上·河南南阳·阶段练习)集合y|y=6x+2,x∈Z,y∈Z中的元素个数为( )
A.2B.4C.6D.8
3.(22-23高三上·天津河西·期中)含有3个实数的集合既可表示成a,ba,1,又可表示成a2,a+b,0,则a2022+b2022= .
考点三、集合的基本关系
1.(2024·陕西商洛·模拟预测)在下列选项中,能正确表示集合A={−3,0,3}和B=x|x2+3x=0的关系的是( )
A.A=BB.A⊇BC.A⊆BD.A∩B=∅
2.(2024·辽宁·三模)若全集U=R,A=xx<2,B=yy=ex,x∈R,则下列关系正确的是( )
A.A⊆BB.B⊆AC.B⊆∁UAD.∁UA⊆B
1.(2024·重庆·三模)已知集合A={x|x2−1=0},集合B=a+1,a−1,3,若A⊆B,则a=( )
A.−1B.0C.1D.2
2.(2024·河南信阳·模拟预测)已知集合A={x|bx=a,a,b∈R},B={b,1b},A⊆B,则a的取值集合为 .
3.(23-24高三下·河南郑州·阶段练习)已知集合A=x∣x2−3x<0,B={x∣−2
1.(2024·安徽·模拟预测)已知集合A=x∈N2x2−5x≤0,则A的子集个数为( )
A.4B.7C.8D.16
2.(23-24高三下·辽宁·阶段练习)已知集合A=0,1,2,3,B=xy=ln−x2+4x,则A∩B子集的个数为( )
A.4B.8C.15D.16
1.(2024·安徽安庆·二模)若集合P=x∣−2≤x
2.(2024·湖北武汉·模拟预测)设集合A=eln2,ln44,B=2,lne3,ln22,则A∪B的子集个数为( )
A.2B.4C.8D.16
3.(2024·福建泉州·模拟预测)设集合M=x∈Zx−2x+3<0,则集合M的非空真子集个数为( )
A.16B.15C.14D.13
4、(2024·天津和平·一模)已知集合A=x∈N−2≤x<2,B=x∈Zx<2,集合C=A∩B,则集合C的子集个数为( )
A.1B.2C.3D.4
考点五、集合的并交补运算
1. (2023·天津·高考真题)已知集合U=1,2,3,4,5,A=1,3,B=1,2,4,则∁UB∪A=( )
A.1,3,5B.1,3C.1,2,4D.1,2,4,5
2. (2024·天津·高考真题)集合A=1,2,3,4,B=2,3,4,5,则A∩B=( )
A.1,2,3,4B.2,3,4C.2,4D.1
1.(2024·北京·高考真题)已知集合M={x|−3
C.x|−3
3.(2024·全国·高考真题)已知集合A=1,2,3,4,5,9,B=xx∈A,则∁AA∩B=( )
A.1,4,9B.3,4,9C.1,2,3D.2,3,5
4.(2024·全国·高考真题)若集合A=1,2,3,4,5,9,B=xx+1∈A,则A∩B=( )
A.1,3,4B.2,3,4C.1,2,3,4D.0,1,2,3,4,9
5.(2023·全国·高考真题)设全集U=Z,集合M={x∣x=3k+1,k∈Z},N={x∣x=3k+2,k∈Z},∁U(M∪N)=( )
A.{x|x=3k,k∈Z}B.{x∣x=3k−1,k∈Z}
C.{x∣x=3k−2,k∈Z}D.∅
6.(2023·全国·高考真题)设集合U=R,集合M=xx<1,N=x−1
C.∁UM∩ND.M∪∁UN
7.(2023·全国·高考真题)设全集U=1,2,3,4,5,集合M=1,4,N=2,5,则N∪∁UM=( )
A.2,3,5B.1,3,4C.1,2,4,5D.2,3,4,5
考点六、Venn图的运用
1.(2024·湖南邵阳·三模)已知全集U=R,集合A=x−1≤x≤2,B=x1≤x≤6,如图所示,则图中阴影部分表示的集合是( )
A.x−1≤x≤6B.xx<−1C.xx>6D.xx<−1或x>6
2.(2024·湖北黄冈·二模)已知集合A=x∈N∣x−3x+2≤0,B=x∣x−1≤1,则图中阴影部分表示的集合为( )
A.0,1B.3C.1,2D.1,2,3
1.(23-24高三下·重庆·阶段练习)如图所示,U是全集,A,B是U的子集,则阴影部分所表示的集合是( )
A.∁UA∪BB.A∪∁UBC.∁UA∩∁UBD.∁UA∪∁UB
2.(2024·山西·三模)已知集合A,B均为集合U的子集,则∁UA∩B表示的区域为( )
A.①B.②C.③D.④
3.(2024·陕西咸阳·模拟预测)如图所示的Venn图中,A、B是非空集合,定义集合A⊗B为阴影部分表示的集合.若A=x∈Zx2−3x−4<0,B=x∈Zx≤2,则A⊗B=( )
A.−1,0,3B.−2,−1,2
C.−2,−1,2,3D.−2,−1,3
4.(2024·广西柳州·三模)某中学的学生积极参加体育锻炼,其中有90%的学生喜欢足球或游泳,60%的学生喜欢足球,80%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
A.70%B.60%C.50%D.40%
5.(2023·四川南充·一模)已知全集U=R,集合A=xlg3(x−1)>1,B=xx24+y2=1,则能表示A,B,U关系的图是( )
A. B.
C. D.
考点七、充分条件与必要条件
1.(2024·天津·高考真题)设a,b∈R,则“a3=b3”是“3a=3b”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
2.(2022·天津·高考真题)“x为整数”是“2x+1为整数”的( )条件
A.充分不必要B.必要不充分C.充分必要D.既不充分也不必要
1.(2024·全国·高考真题)设向量a=x+1,x,b=x,2,则( )
A.“x=−3”是“a⊥b”的必要条件B.“x=−3”是“a//b”的必要条件
C.“x=0”是“a⊥b”的充分条件D.“x=−1+3”是“a//b”的充分条件
2.(2023·北京·高考真题)若xy≠0,则“x+y=0”是“yx+xy=−2”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
3.(2023·全国·高考真题)设甲:sin2α+sin2β=1,乙:sinα+csβ=0,则( )
A.甲是乙的充分条件但不是必要条件B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件D.甲既不是乙的充分条件也不是乙的必要条件
4.(2023·天津·高考真题)已知a,b∈R,“a2=b2”是“a2+b2=2ab”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分又不必要条件
5.(2023·全国·高考真题)记Sn为数列an的前n项和,设甲:an为等差数列;乙:{Snn}为等差数列,则( )
A.甲是乙的充分条件但不是必要条件
B.甲是乙的必要条件但不是充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件也不是乙的必要条件
6.(2024·天津·模拟预测)已知p:x2+2x−3<0,q:x2+x−2<0,则p是q的( )条件
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分又不必要条件
考点八、全称量词命题与存在量词命题、
1.(2024·全国·高考真题)已知命题p:∀x∈R,|x+1|>1;命题q:∃x>0,x3=x,则( )
A.p和q都是真命题B.¬p和q都是真命题
C.p和¬q都是真命题D.¬p和¬q都是真命题
2.(2020·山东·高考真题)下列命题为真命题的是( )
A.1>0且3>4B.1>2或4>5
C.∃x∈R,csx>1D.∀x∈R,x2≥0
1.(22-23高三上·天津滨海新·期中)若命题“∀x∈R,m≥sinx+csx”是真命题,则实数m的取值范围是 .
2.(2022高三上·河南·专题练习)已知命题p:∀x∈R,ex+1+e3−x≥2e2,则命题p的真假以及否定分别为( )
A.真,¬p:∀x∈R,ex+1+e3−x<2e2B.假,¬p:∀x∈R,ex+1+e3−x<2e2
C.真,¬p:∃x∈R,ex+1+e3−x<2e2D.假,¬p:∃x∈R,ex+1+e3−x<2e2
3.(22-23高三上·北京东城·开学考试)使得命题“∀x∈R,kx2+2kx−3<0”为真命题的k的取值范围( )
A.(−3,0)B.(−3,0]
C.(−3,1)D.(3,+∞)
4.(2024·陕西安康·模拟预测)已知命题p:∀x∈−1,0,a≤12x−5x,若p为假命题,则a的取值范围是
5.(2024·四川凉山·二模)已知命题“∀x∈R,sin2π+x+2csx+m≤0”是假命题,则m的取值范围为( )
A.−2,+∞B.−2,+∞C.−∞,−1D.−∞,−2
1.(2024·甘肃兰州·三模)设集合A={0,1,2},B={3,m},若A∩B={2},则A∪B=( )
A.{0,1,2,3}B.{0,1,2}C.{1,2,3}D.{2,3}
2.(2024·黑龙江哈尔滨·模拟预测)命题p:∀x>0,x2−ax+2>0的否定是( )
A.∀x>0,x2−ax+2≤0B.∀x≤0,x2−ax+2>0
C.∃x0>0,x02−ax0+2≤0D.∃x0≤0,x02−ax0+2≤0
3.(2024·山东青岛·三模)已知命题 p:∀x∈0,π2,sinx
C.∃x∉0,π2,sinx≥xD.∃x∈0,π2,sinx≥x
4.(2024·江苏苏州·三模)已知集合A={x∣sinx>0},B={x||x−3∣<1},则A∩B=( )
A.{x∣2
A.x−2≤x≤1B.x−2
6.(23-24高三下·湖南岳阳·期中)已知集合A=xx>4,B={x∈Z|3<x<7},则A∩B=( )
A.4,6B.4,7C.4,5,6,7D.5,6
7.(2024·河南·模拟预测)已知集合A=0,1,2,B=x∈Z−2
1.(2025·甘肃张掖·模拟预测)设Sn为数列an的前n项和,q≠0,a1≠0,则“1−qSn=a11−qn”是“数列an是以q为公比的等比数列”的( )
A.充要条件B.充分不必要条件
C.必要不充分条件D.既不充分也不必要条件
2.(2025·甘肃张掖·模拟预测)已知非空集合A={xx
A.0,1B.0,1C.1,+∞D.1,+∞
3.(2024·甘肃兰州·三模)已知a,b均为正实数,则“1a>1b”是“a2+2b2>3ab”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
4.(2024·江苏扬州·模拟预测)已知集合A=0,a2,B=1,a+1,a−1,则“a=1”是“A⊆B”的( )
A.必要不充分条件B.充分不必要条件
C.充要条件D.既不充分也不必要条件
5.(2024·湖南邵阳·三模)“0
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
6.(2024·广西贵港·模拟预测)已知集合A=x|x−4x+2≤0,B={x|y=lg3(x2−9)},则A∩(∁RB)=( )
A.[−2,3]B.(−2,3]C.(−2,4]D.[3,4]
7.(2024高三下·全国·专题练习)已知集合A=x|x2−x−12≤0,B=x|x2−3mx+2m2+m−1<0,若“x∈A”是“x∈B”的必要不充分条件,则实数m的取值范围为 .
1.(2022·天津·高考真题)设全集U=−2,−1,0,1,2,集合A=0,1,2,B=−1,2,则A∩∁UB=( )
A.0,1B.0,1,2C.−1,1,2D.0,−1,1,2
2.(2022·浙江·高考真题)设集合A={1,2},B={2,4,6},则A∪B=( )
A.{2}B.{1,2}C.{2,4,6}D.{1,2,4,6}
3.(2002·江苏·高考真题)设集合M=x|x=k2+14,k∈Z,N=x|x=k4+12,k∈Z,则( )
A.M=NB.M⊆NC.M⊇ND.M∩N=∅
4.(2022·全国·高考真题)集合M=2,4,6,8,10,N=x−1
5.(2022·全国·高考真题)设集合A={−2,−1,0,1,2},B=x∣0≤x<52,则A∩B=( )
A.0,1,2B.{−2,−1,0}C.{0,1}D.{1,2}
6.(2022·全国·高考真题)设全集U={−2,−1,0,1,2,3},集合A={−1,2},B=x∣x2−4x+3=0,则∁U(A∪B)=( )
A.{1,3}B.{0,3}C.{−2,1}D.{−2,0}
7.(2022·北京·高考真题)已知全集U={x−3
8.(2021·天津·高考真题)设集合A=−1,0,1,B=1,3,5,C=0,2,4,则(A∩B)∪C=( )
A.0B.{0,1,3,5}C.{0,1,2,4}D.{0,2,3,4}
5年考情
考题示例
考点分析
2024年天津卷,第1题,5分
交集的概念与运算
2024年天津卷,第2题,5分
充分条件的判定及性质、必要条件的判定及性质、比较指数幂的大小、判断一般幂函数的单调性
2023年天津卷,第1题,5分
并交补混合运算
2023年天津卷,第2题,5分
必要条件的判断与性质
2022年天津卷,第1题,5分
交集的概念及运算、交并补混合运算
2022年天津卷,第2题,5分
判断命题的充分与必要条件
2021年天津卷,第1题,5分
并交补混合运算
2021年天津卷,第2题,5分
判断命题的充分与必要条件
2020年天津卷,第1题,5分
并交补混合运算
2020年天津卷,第2题,5分
判断命题的充分与必要条件
名称
记号
意义
性质
示意图
子集
A⊆B(或B⊇A)
A中的任一元素都属于B
(1)A⊆A
(2)∅⊆A
(3)若A⊆B且B⊆C,则A⊆C
(4)若A⊆B且B⊆A,则A=B
或
真子集
A⊂≠B(或B⊃≠A)
A⊆B,且B中至少有一元素不属于A
(1)∅⊂≠A(A为非空子集)(2)若A⊂≠B且B⊂≠C,则A⊂≠C
集合相等
A=B
A中的任一元素都属于B,B中的任一元素都属于A
(1)A⊆B(2)B⊆A
相关学案
这是一份2025年高考数学一轮复习讲义 考点归纳与方法总结 第01讲 集合(精讲)(含解析),共30页。学案主要包含了必备知识整合,集合间的基本关系,集合的基本运算等内容,欢迎下载使用。
这是一份考点01 集合6种常见考法归类(解析版)-【考点通关】备战2024年高考数学一轮题型归纳与解题策略(新高考地区专用),共42页。学案主要包含了集合的含义与表示,集合间的基本关系,集合的基本运算,韦恩图及其应用,集合的新定义问题,集合的综合应用等内容,欢迎下载使用。
这是一份考向01 集合(重点)-备战2022年高考数学一轮复习考点微专题学案(新高考地区专用),共9页。学案主要包含了知识拓展等内容,欢迎下载使用。












