



所属成套资源:备战2025年高考数学一轮复习考点帮(天津专用)
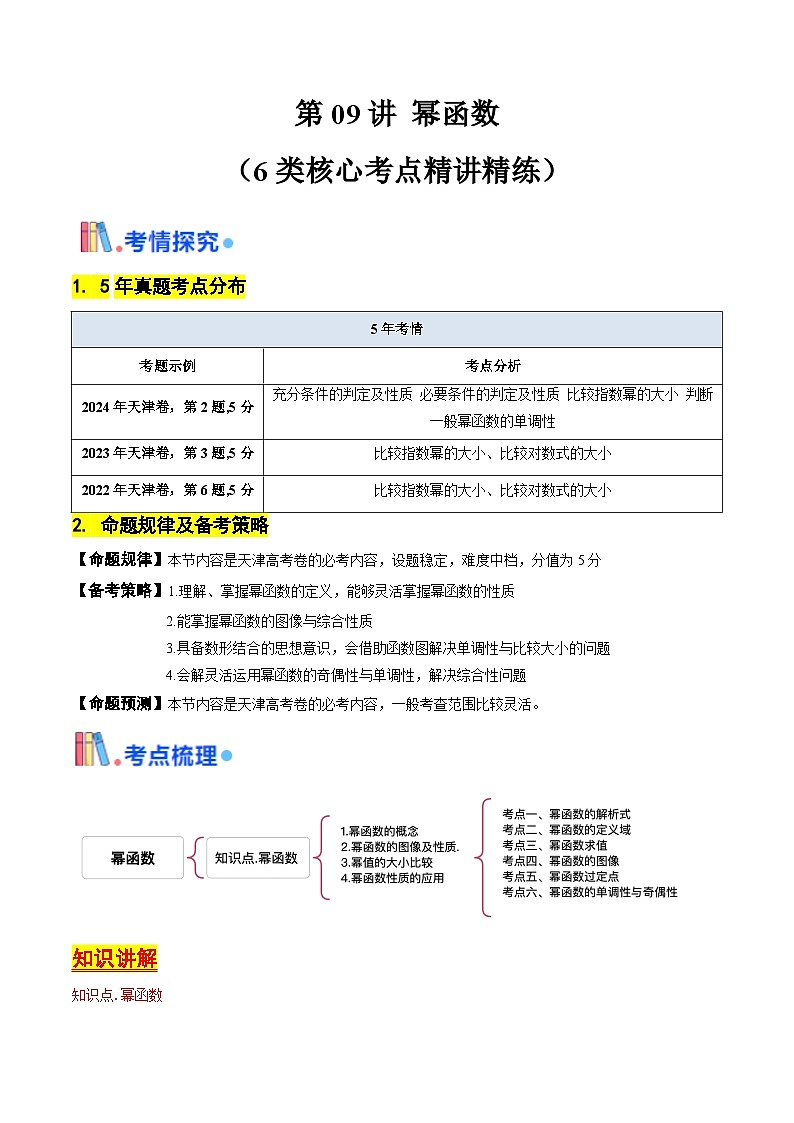
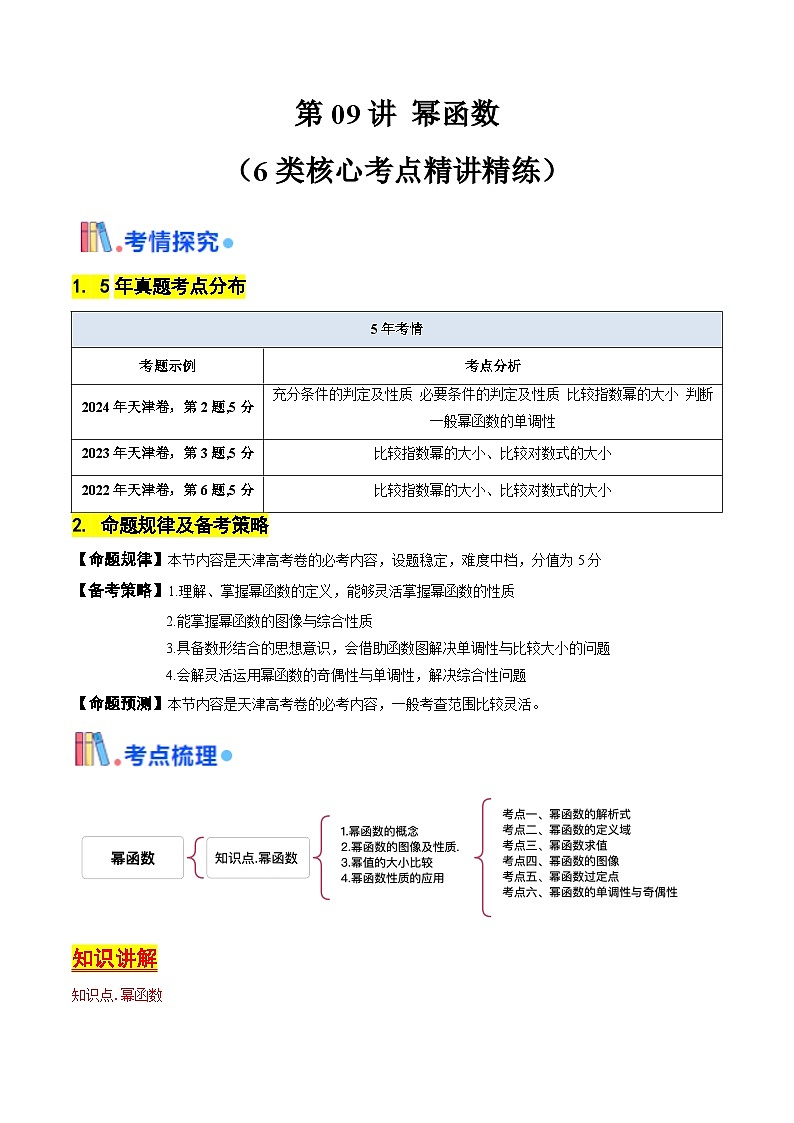
第09讲 幂函数(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案
展开这是一份第09讲 幂函数(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案,文件包含第09讲幂函数教师版备战2025年高考数学一轮复习考点帮天津专用docx、第09讲幂函数学生版备战2025年高考数学一轮复习考点帮天津专用docx等2份学案配套教学资源,其中学案共29页, 欢迎下载使用。
1. 5年真题考点分布
2. 命题规律及备考策略
【命题规律】本节内容是天津高考卷的必考内容,设题稳定,难度中档,分值为5分
【备考策略】1.理解、掌握幂函数的定义,能够灵活掌握幂函数的性质
2.能掌握幂函数的图像与综合性质
3.具备数形结合的思想意识,会借助函数图解决单调性与比较大小的问题
4.会解灵活运用幂函数的奇偶性与单调性,解决综合性问题
【命题预测】本节内容是天津高考卷的必考内容,一般考查范围比较灵活。
知识讲解
知识点.幂函数
1.概念:形如y=xα(α∈R)的函数称为幂函数,其中x是自变量,α是常数
2.幂函数的图像及性质.
y=1x, y=x12, y=x2, y=x3, y=x
3.幂值的大小比较
(1)直接法:当幂指数相同时,可直接利用幂函数的单调性来比较.
(2)转化法:当幂指数不同时,可以先转化为相同幂指数,再运用单调性比较大小.
(3)中间值法:当底数不同且幂指数也不同而不能运用单调性比较大小时,可选取适当的中间值与两数分别比较,从而达到比较大小的目的.
4.幂函数性质的应用
利用幂函数的性质解不等式,实际上就是利用幂函数的单调性,将不等式的大小关系转化为自变量的大小关系,解不等式(组)求参数范围时,注意分类讨论思想的应用.
考点一、幂函数的解析式
1.(2024·广东广州·模拟预测)若幂函数fx=m2−m−1x2m−3在0,+∞上单调递增,则实数m的值为( )
A.2B.1C.−1D.−2
2.(2023·四川成都·一模)已知幂函数fx=xα的图象过点P3,9,则α=( )
A.12B.1C.2D.3
1.(23-24高三上·陕西咸阳·阶段练习)已知幂函数fx=2m2−mxm−12在区间0,+∞上单调递增,则m=( )
A.-2B.1C.−12D.-1
2.(23-24高三上·青海西宁·阶段练习)若幂函数f(x)=xα的图象经过点(4,12),则α2= .
3.(2024·山东日照·二模)已知幂函数的图象过点2,4,则函数的解析式为( )
A.y=2xB.y=x2C.y=lg2xD.y=sinx
考点二、幂函数的定义域
1.(2022·上海·模拟预测)下列函数定义域为R的是( )
A.y=x−12B.y=x−1C.y=x13D.y=x12
2.(23-24高三上·上海静安·期中)函数y=3x−2−34的定义域为 .
1.(23-24高三下·上海松江·阶段练习)若函数fx=x−m2+2m+3m∈Z的定义域为R,且fx+1=f−x−1,则实数m的值为
2.(22-23高三下·上海浦东新·阶段练习)设m∈R,若幂函数y=xm2−2m+1定义域为R,且其图像关于y轴成轴对称,则m的值可以为( )
A.1B.4C.7D.10
考点三、幂函数求值
1.(2024高三·全国·专题练习)若幂函数y=fx的图象经过点2,2,则f16=( )
A.2B.2C.4D.12
2.(22-23高三上·福建宁德·阶段练习)已知函数y=lgax−3+2(a>0且a≠1)的图象恒过定点P,点P在幂函数y=fx的图象上,则f4=( )
A.−2B.2C.1D.−1
1. (2023·全国·模拟预测)已知函数fx=lg2x+1,x≥1x2,x<1,若fa=2,则a的值为( )
A.2或−2B.2或2C.2或−2D.1或2
2.(23-24高三上·四川眉山·期中)已知幂函数fx=m2+m−1xm的图象与坐标轴没有公共点,则f2=
3.(22-23高三上·江苏盐城·阶段练习)若函数y=ax−2+3(a>0且a≠1)的图象恒过定点Q,且点Q在幂函数f(x)=xm的图象上,则f(4)= .
考点四、幂函数的图像
1.(2024·天津·模拟预测)下列图象中,不可能成为函数fx=x3+tx的图象的是( )
A.B.
C.D.
2.(2024·四川南充·二模)已知函数fx的图象如图所示,则fx的解析式可能是( )
A.y=x12B.y=x−12C.y=x3D.y=x13
1.(2023·湖南岳阳·模拟预测)如图,已知幂函数y=xa,y=xb,y=xc在0,+∞上的图象分别是下降,急速上升,缓慢上升,则( )
A.c
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
3.(22-23高三上·上海浦东新·阶段练习)如图所示是函数y=xmn(m,n均为正整数且m,n互质)的图象,则( )
A.m,n是奇数且mn<1
B.m是偶数,n是奇数,且mn<1
C.m是偶数,n是奇数,且mn>1
D.m,n是奇数,且mn>1
考点五、幂函数过定点
1.(21-22高三上·河南·阶段练习)已知p:fx是幂函数,q:fx图象过点0,0,则p是q的( )
A.充要条件B.充分不必要条件
C.必要不充分条件D.既不充分也不必要条件
2.(2022·四川乐山·一模)已知幂函数f(x)=xα和g(x)=xβ,其中α>β>0,则有下列说法:
①f(x)和g(x)图象都过点1,1;
②f(x)和g(x)图象都过点(−1,1);
③在区间[1,+∞)上,增长速度更快的是f(x);
④在区间[1,+∞)上,增长速度更快的是g(x).
则其中正确命题的序号是( )
A.①③B.②③C.①④D.②④
1.(22-23高三上·上海徐汇·期末)当α∈R时,函数y=xα−2的图象恒过定点A,则点A的坐标为 .
2.(22-23高三上·陕西渭南·阶段练习)已知函数fx=2+xa(a为不等于0的常数)的图象恒过定点P,则P点的坐标为 .
考点六、幂函数的单调性与奇偶性
1.(2024·广西·二模)下列函数中,在0,2上单调递增的是( )
A.fx=x−1B.fx=x2−2x
C.fx=1xD.fx=x14
2.(2024·北京朝阳·一模)已知a∈R,则“0
C.充要条件D.既不充分也不必要条件
1.(2024·湖南常德·三模)已知奇函数y=f(x)是定义域为R的连续函数,且在区间(0,+∞)上单调递增,则下列说法正确的是( )
A.函数y=f(x)+x2在R上单调递增
B.函数y=f(x)−x2在(0,+∞)上单调递增
C.函数y=x2f(x)在R上单调递增
D.函数y=f(x)x2在(0,+∞)上单调递增
2.(23-24高三上·安徽·阶段练习)已知幂函数fx=m2−5m+5xm−2是R上的偶函数,且函数gx=fx−2a−6x在区间1,3上单调递增,则实数a的取值范围是( )
A.−∞,4B.−∞,4
C.6,+∞D.−∞,4∪6,+∞
3.(2023·四川南充·模拟预测)已知幂函数fx=xmnm,n∈Z,下列能成为“fx是R上的偶函数”的充分条件的是( )
A.m=−3,n=1B.m=1,n=2
C.m=2,n=3D.m=1,n=3
4.(23-24高三下·上海·阶段练习)已知集合A=xx+2x−5<0,B=−3,−2,−1,0,1,2,3,任取k∈A∩B,则y=xk为偶函数的概率为 .
1.(2024·重庆·模拟预测)已知函数f(x)=xα(x>0),α为实数,f(x)的导函数为f'(x),在同一直角坐标系中,f(x)与f'(x)的大致图象不可能是( )
A.B.
C.D.
2.(2024高二下·湖南娄底·学业考试)函数y=x3的大致图像是( )
A.B.C.D.
3.(2024·四川成都·模拟预测)设命题p:∃m∈R,使fx=m−1xm2−4m+3是幂函数,且在0,+∞上单调递减;命题q:∀x∈2,+∞,2x>x2,则下列命题为真的是( )
A.p∧¬qB.¬p∧qC.p∧qD.¬p∨q
4.(2024·陕西西安·二模)下列函数中,既是奇函数又在−∞,+∞上单调递减的是( )
A.y=1xB.y=x3
C.y=−xxD.y=3−x
5.(2024高三·全国·专题练习)已知α∈−2,−1,−12,12,1,2,3.若幂函数f(x)=xα为奇函数,且在(0,+∞)上递减,则α= .
6.(2024高三·全国·专题练习)已知函数fx=lgax−1+3的图象经过定点A,且幂函数gx的图象过点A,则g12= .
7.(2022高三·全国·专题练习)已知幂函数y=f(x)的图象过点(4,2),令an=f(n+1)+f(n),n∈N∗,记数列1an的前n项和为Sn,则S35= .
1.(23-24高三上·广东深圳·期末)已知实数m,n满足(m+1)3+m=(n−1)3+n=0,则nm=( )
A.-1B.1C.-2D.2
2.(2022·全国·模拟预测)设函数fx=x,0
3.(23-24高三上·安徽·期中)函数fx=x3−x2x+1在−2,2上的图象大致为( )
A. B. C. D.
4.(2024·陕西安康·模拟预测)已知命题p:函数f(x)=x−m2+m在区间(0,+∞)上单调递增,命题q:m
6.(2024·北京延庆·一模)已知函数f(x)=xα(0<α<1)在区间(−1,0)上单调递减,则α的一个取值为 .
7.(23-24高三上·宁夏吴忠·阶段练习)设fx=x,0
2.(·陕西·高考真题)下了函数中,满足“fx+y=fxfy”的单调递增函数是( )
A.fx=x3B.fx=3x
C.fx=x23D.fx=12x
3.(·湖北·高考真题)设x∈R,[x]表示不超过x 的最大整数.若存在实数t,使得[t]=1,[t2]=2,…,[tn]=n同时成立,则正整数n的最大值是
A.3B.4C.5D.6
4.(2023·天津·高考真题)设a=1.010.5,b=1.010.6,c=0.60.5,则a,b,c的大小关系为( )
A.a
A.−1,1;B.−1,+∞;
C.−∞,−2∪0,+∞;D.−∞,−1∪1,+∞.
5年考情
考题示例
考点分析
2024年天津卷,第2题,5分
充分条件的判定及性质 必要条件的判定及性质 比较指数幂的大小 判断一般幂函数的单调性
2023年天津卷,第3题,5分
比较指数幂的大小、比较对数式的大小
2022年天津卷,第6题,5分
比较指数幂的大小、比较对数式的大小
y=x
y=x2
y=x3
y=x12
y=x−1
定义域
R
R
R
[0,+∞)
{ x| xϵR且x≠0 }
值域
R
[0,+∞)
R
[0,+∞)
{y| yϵR且y≠0 }
奇偶性
奇函数
偶函数
奇函数
非奇非偶函数
奇函数
单调性
增
x∈[0,+∞)时,增;
x∈(-∞,0]时,减.
增
增
x∈(0,+∞)时,减;
x∈(-∞,0)时,增.
相关学案
这是一份第24讲 数列的概念(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案,文件包含第24讲数列的概念教师版备战2025年高考数学一轮复习考点帮天津专用docx、第24讲数列的概念学生版备战2025年高考数学一轮复习考点帮天津专用docx等2份学案配套教学资源,其中学案共48页, 欢迎下载使用。
这是一份第23讲 复数(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案,文件包含第23讲复数教师版备战2025年高考数学一轮复习考点帮天津专用docx、第23讲复数学生版备战2025年高考数学一轮复习考点帮天津专用docx等2份学案配套教学资源,其中学案共35页, 欢迎下载使用。
这是一份第13讲函数的极值(含答案) 备战2025年高考数学一轮复习考点帮(天津专用)学案,文件包含第13讲函数的极值教师版备战2025年高考数学一轮复习考点帮天津专用docx、第13讲函数的极值学生版备战2025年高考数学一轮复习考点帮天津专用docx等2份学案配套教学资源,其中学案共54页, 欢迎下载使用。












