第14章 整式的乘法与因式分解 人教版八年级上册 第10课时　乘法公式(2)——完全平方公式课件

这是一份第14章 整式的乘法与因式分解 人教版八年级上册 第10课时　乘法公式(2)——完全平方公式课件，共23页。
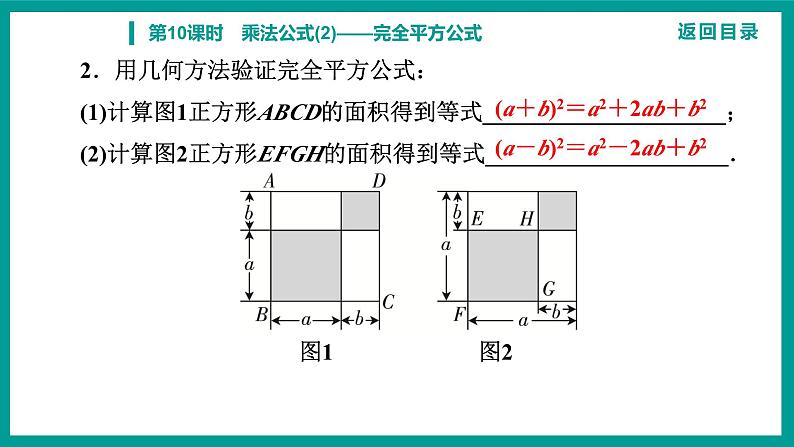
一、几何背景下的多结论问题第十四章　整式的乘法与因式分解第10课时　乘法公式(2)——完全平方公式理解乘法公式(a±b)2＝a2±2ab＋b2，了解公式的几何背景，能利用公式进行简单的计算和推理．(核心素养：抽象能力、运算能力、几何直观)课标要求知识导学1.填空：(1)(p＋1)2＝(p＋1)(p＋1)＝____________；(2)(p－1)2＝(p－1)(p－1)＝____________；(3)(m＋2)2＝(m＋2)(m＋2)＝____________；(4)(m－2)2＝(m－2)(m－2)＝____________．完全平方公式：两个数的和(或差)的平方，等于它们的_________，加上(或减去)它们的__________，即(a＋b)2＝____________，或(a－b)2＝____________．p2＋2p＋1p2－2p＋1m2＋4m＋4m2－4m＋4平方和积的2倍a2＋2ab＋b2a2－2ab＋b22．用几何方法验证完全平方公式：(1)计算图1正方形ABCD的面积得到等式_____________________；(2)计算图2正方形EFGH的面积得到等式_____________________．图1　　　　　 　图2(a＋b)2＝a2＋2ab＋b2(a－b)2＝a2－2ab＋b2课堂讲练 完全平方公式的直接运用例1　计算：(1)(m－3)2； (2)(3x－2)2； (3)(2－3x)2； (4)(2a＋5b)2.思考：比较(2)和(3)，你能发现什么？解：(1)原式＝m2－2·m·3＋32＝m2－6m＋9.(2)原式＝(3x)2－2·3x·2＋22＝9x2－12x＋4.(3)原式＝22－2×2·3x＋(3x)2＝9x2－12x＋4.(4)原式＝(2a)2＋2·2a·5b＋(5b)2＝4a2＋20ab＋25b2.训练　1.计算：(1)(5＋a)2 ； 　 (3)(4a＋3b)2 ； (4)(－4a－3b)2.思考：比较(3)和(4)，你能发现什么？解：(1)原式＝52＋2×5·a＋a2＝a2＋10a＋25.(3)原式＝(4a)2＋2·4a·3b＋(3b)2＝16a2＋24ab＋9b2.(4)原式＝(－4a)2＋2·(－4a)·(－3b)＋(－3b)2＝16a2＋24ab＋9b2.　1.完全平方公式的口诀：首平方，尾平方，2倍乘积在中央．2．完全平方公式的变形：(1)(a－b)2＝(b－a)2；(2)(－a－b)2＝(a＋b)2 . 用完全平方公式进行简便计算例2　计算：1012.训练　2.计算：972.解：原式＝(100＋1)2＝1002＋2×100×1＋12＝10 000＋200＋1＝10 201.解：原式＝(100－3)2＝1002－2×100×3＋32＝10 000－600＋9＝9 409. 完全平方公式的常见变形例3　已知a－b＝10，ab＝20，求a2＋b2的值．解：∵a－b＝10，ab＝20，∴a2＋b2＝(a－b)2＋2ab＝102＋2×20＝140.训练　3.已知2m＋n＝3，mn＝－1，求(2m－n)2的值．解：∵2m＋n＝3，mn＝－1，∴(2m－n)2＝(2m＋n)2－8mn＝32－8×(－1)＝17.　完全平方公式的常见变形：(1)a2＋b2＝(a＋b)2－2ab＝(a－b)2＋2ab；(2)(a＋b)2－(a－b)2＝4ab；(3)(a＋b)2＋(a－b)2＝2(a2＋b2).课堂检测1．填空：(1)(1－2a)2＝______________； (2)(mn＋3)2＝______________．2．若(x＋2)2＝x2＋mx＋4，则m的值为__________.1－4a＋4a2m2n2＋6mn＋94 (2)(－5x＋2y)2.(2)原式＝(－5x)2＋2·(－5x)·2y＋(2y)2＝25x2－20xy＋4y2.4．先化简，再求值：(2y＋1)2－(y－1)(y＋5)，其中y＝2.解：原式＝4y2＋4y＋1－(y2＋5y－y－5)＝4y2＋4y＋1－y2－4y＋5＝3y2＋6.当y＝2时，原式＝3×22＋6＝18.5．已知(x－y)2＝4，(x＋y)2＝64，求下列各式的值：(1)x2＋y2；(2)xy.解：(x－y)2＝x2－2xy＋y2＝4，①(x＋y)2＝x2＋2xy＋y2＝64.②(1)①＋②，得2x2＋2y2＝68.∴x2＋y2＝34.(2)②－①，得4xy＝60.∴xy＝15.6．【数学文化】我国南宋数学家杨辉发现的“杨辉三角”揭示了(a＋b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的项数及各项系数的有关规律．如图3，在“杨辉三角”中第3行的三个数1，2，1恰好对应(a＋b)2的展开式的系数．请根据“杨辉三角”的规律，回答下列问题：(1)(a＋b)n的展开式共有__________项；(2)请写出多项式(a＋b)5的展开式．图3(n＋1)解：(a＋b)5＝a5＋5a4b＋10a3b2＋10a2b3＋5ab4＋b5.随堂测课时练1．计算：(1)(a＋2)2＝__________； (2)(3x－y)2＝______________；(4)(－4x＋2y)2＝_________________.2．若(x－4)2＝x2＋kx＋16，则k的值是______.a2＋4a＋49x2－6xy＋y216x2－16xy＋4y2－83．计算：(1)(x－y)2＋x(x＋2y)；(2)(2x－y)2－(x＋2y)(x－2y)－(3x＋y)(x＋y).解：(1)原式＝x2－2xy＋y2＋x2＋2xy＝2x2＋y2.(2)原式＝4x2－4xy＋y2－(x2－4y2)－(3x2＋4xy＋y2)＝4x2－x2－3x2－4xy－4xy＋y2＋4y2－y2＝－8xy＋4y2.4．简便计算：1032.解：原式＝(100＋3)2＝1002＋2×100×3＋32＝10 000＋600＋9＝10 609.5．已知(a＋b)2＝49，a2＋b2＝25，求下列各式的值：(1)ab; (2)(a－b)2.解：(1)∵(a＋b)2＝a2＋2ab＋b2＝25＋2ab＝49，∴ab＝12.(2)(a－b)2＝a2－2ab＋b2＝25－2ab＝25－24＝1.循环练6．计算：(2a－1)(a＋2)－6a3b÷3ab.解：原式＝2a2＋4a－a－2－2a2＝3a－2.