苏科版（2024）八年级上册2.4 线段、角的轴对称性公开课ppt课件

这是一份苏科版（2024）八年级上册2.4 线段、角的轴对称性公开课ppt课件，共36页。PPT课件主要包含了线段PC的长，PAPB，角平分线的性质定理，符号语言，BDCD，角平分线的判定定理等内容，欢迎下载使用。

1. 探索并证明角平分线的性质定理和判定定理；
2.了解角平分线是具有特殊性质的点的集合.
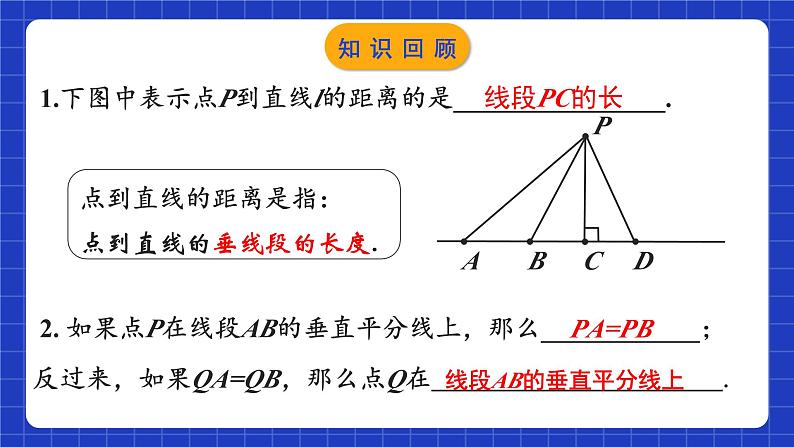
1.下图中表示点P到直线l的距离的是________________.
点到直线的距离是指：点到直线的垂线段的长度.
2. 如果点P在线段AB的垂直平分线上，那么____________；
反过来，如果QA=QB，那么点Q在______________________.
线段AB的垂直平分线上
操作1 在一张薄纸上画∠AOB．
活动一 探究角的轴对称性
操作2 折叠纸片使角的两边重合．
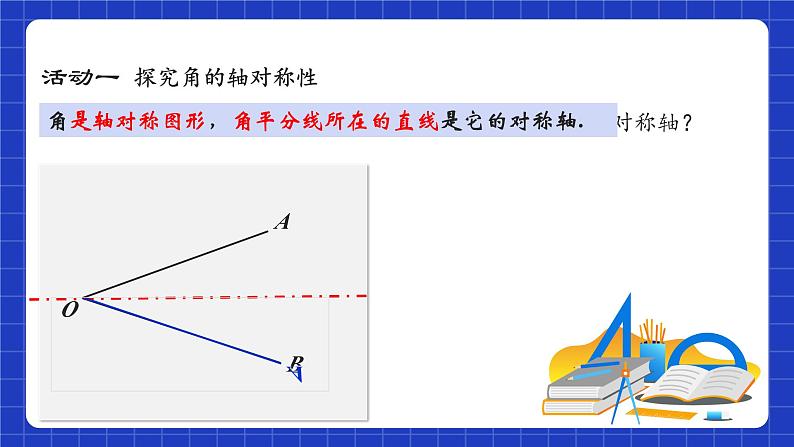
思考 它是轴对称图形吗？对称轴在哪里？如何描述角的对称轴？
角是轴对称图形，角平分线所在的直线是它的对称轴.
活动二 探究角平分线性质
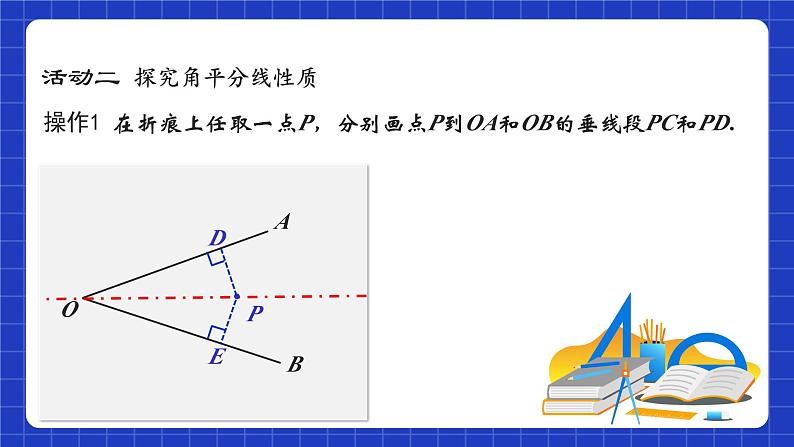
操作1 在折痕上任取一点P，分别画点P到OA和OB的垂线段PC和PD.
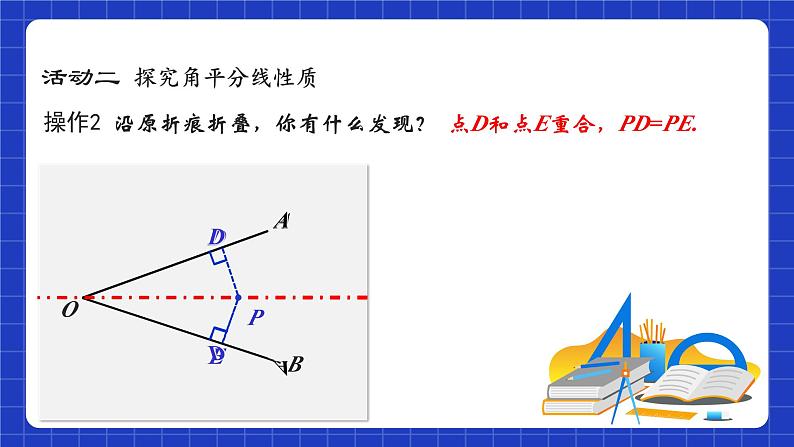
操作2 沿原折痕折叠，你有什么发现？
点D和点E重合，PD=PE.
思考1 你能利用角的轴对称性验证你的结论吗？
理由如下：把△POD沿OP翻折，∵∠AOP=∠BOP，∴OA与OB重合．∵PD⊥OA，PE⊥OB，依据基本事实“过一点有且只有一条直线与已知直线垂直”，∴PD与PE重合，∴PD=PE．
思考2 你还有其他的证明方法吗？
思考3 像这样的点P还有吗？为什么？
角平分线上的点 到角两边的距离相等．
∵OC平分∠AOB，点P在OC上， PD⊥OA，PE⊥OB，
∴PD＝PE（角平分线上的点 到角两边的距离相等）.
注意：一定要表明是两条垂线段.
（1）∵ 如图，AD平分∠BAC（已知）
∴ = ，( ).
角的平分线上的点到这个角的两边的距离相等
BD CD
判断下列的写法是否正确？
理由：没有垂直，不能确定BD、CD是点D到角两边的距离.
(2)∵ 如图， DC⊥AC，DB⊥AB （已知）.
∴ = , ( )
角内任意一条线上的点到这个角的两边的距离相等
理由：无法确定点D在∠BAC的平分线上.
在角平分线上和垂直这两个条件缺一不可．
活动三 探究角平分线的判定方法
讨论1：你能写出角平分线的性质定理的逆命题吗？
猜想：如果一个点到角两边的距离相等，那么这个点在角的平分线上.
角的内部到角的两边距离相等的点在角的平分线上.
求证：角的内部到角的两边距离相等的点在角的平分线上.
已知：如图，若点Q在∠AOB内部，QD⊥OA，QE⊥OB，且QD＝QE，求证：点Q在∠AOB的角平分线上.
∵QD＝QE，QD⊥OA，QE⊥OB，
∴点Q在∠AOB的平分线上 . （角的内部到角两边的距离相等的点在角的平分线上）.
证明点在角平分线上，即可以判定角平分线.
角的内部到角两边的距离相等的点在角的平分线上.
讨论2：如果点到角两边的距离不相等，那么这个点会在这个角的平分线上吗？为什么？
解：这个点不会在这个角的平分线上.理由如下：如图，假设点Q在∠AOB的平分线上，∵QD⊥OA，QE⊥OB，∴ QD =QE．这与QD≠QE矛盾.∴ 如果点到角两边的距离不相等，那么这个点不会在这个角的平分线上.
在角平分线上的点都具有同一个性质而毫无例外;反之,具有这一性质的点都在这个角平分线上而无一遗漏.由此发现了：
角平分线是角的内部到角的两边距离相等的点的集合.
1. 如图，①∵OC平分_______，点P在OC上，PM⊥OA，PN⊥OB，垂足分别为M、N，PM=2，∴PN=　 　 　=　 . ②∵PM⊥OA，PN⊥OB，PM=　　　　，∴点P在∠AOB的平分线上,即OC平分　　　　. 
(1)在BC上找一点P，使点P到AB和AC的距离相等；
(2)在射线AP上找一点Q，使QB=QC.
例 已知：如图，在△ABC中，AD是它的角平分线，且BD=CD，DE⊥AB， DF⊥AC，垂足分别为E、F.求证：EB=FC.
证明： ∵AD是∠BAC的平分线， DE⊥AB，DF⊥AC，
∴ DE=DF，∠DEB=∠DFC=90 °.
∴ Rt△BDE ≌ Rt△CDF(HL).
变式：如图所示，在△ABC中，BD=CD，∠ABD=∠ACD.求证：AD平分∠BAC.
1. 应用角平分线的性质时，“角的平分线”“角平分线上的点到角两边的距离”两个条件缺一不可，不能错用为“角平分线上的点到角两边任意点的距离相等”.
2. 应用角平分线的判定时，需要满足两个条件：“垂直”和“相等”.
3.常用辅助线：过角平分线上一点向两边作垂线段.
一个点：角平分线上的点；二距离：点到角两边的距离；两相等：两条垂线段的长度相等
在一个角的内部，到角两边距离相等的点在这个角的平分线上
常用辅助线：过角平分线上一点向两边作垂线段.
1. 如图，P是∠AOB的平分线OC上一点，PD⊥OB，垂足为D，若PD=2，则点P到边OA的距离是(　　) A.2 B.3 C. 1 D.4
2. 如图，OP平分∠AOB，PA⊥OA，PB⊥OB，垂足分别为A，B.下列结论中不一定成立的是(　　)A．PA＝PB B．PO平分∠APBC．OA＝OB D．AB垂直平分OP
3.如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠CAB交BC于D，DE⊥AB于E，若AB＝6 cm，则△DBE的周长是_____
4.如图，Q是OA上一个动点，点P在∠AOB的平分线上，PD⊥OB于点D，PD=3，则PQ的最小值是　　　　. 
5.如图，AD为△ABC的角平分线，DF⊥AC于点F，∠B=90°，DE=DC.求证：BE=FC.
6.已知：如图，P是OC上一点，PD⊥OA于点D，PE⊥OB于点E，F、G分别是OA、OB上的点，且PF=PG，DF=EG.求证：OC是∠AOB的平分线.