






人教A版 (2019)必修 第一册1.4.2 充要条件备课课件ppt
展开1.4.1 充分条件与必要条件
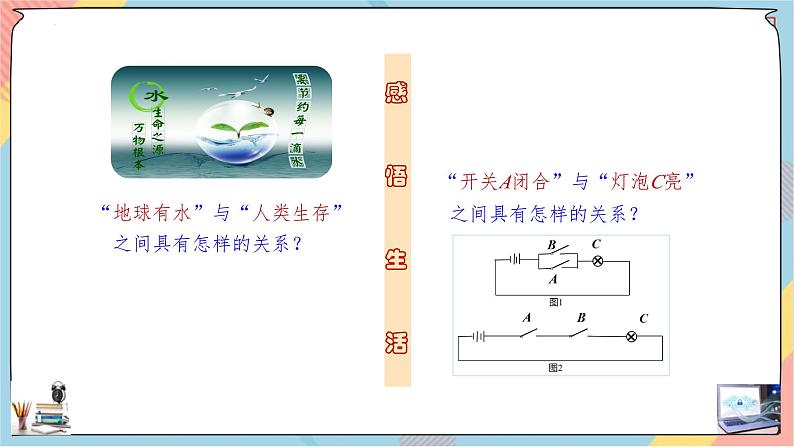
“地球有水”与“人类生存” 之间具有怎样的关系?
“开关A闭合”与“灯泡C亮” 之间具有怎样的关系?
考察下列各组中p与q之间的关系: (1)p: x=1 , q: x2-4x+3=0(2)p: a2 >4 , q: a >2 (3)p: 两个三角形全等 , q: 两个三角形面积相等
(1)中p能推出q,但q推不出p;(2)中p不能推出q,但q能推出p;(3)中p能推出q,但q推不出p.
比如: x=1 是 x2-4x+3=0 的充分条件, 同时,x2-4x+3=0 是 x=1 的必要条件;
a2 >4 不是 a >2 的充分条件, 同时, a >2 不是a2 >4的必要条件
先哲对于“充分”与“必要”的阐释
有之则必然,无之则未必不然
无之则必不然,有之则未必然
用通俗语言阐释“充分”与“必要”
1.下列“若p,则q”形式的命题中,哪些p是q的充分条件?
(2)若x, y为无理数,则xy为无理数;
(4)若四边形的两组对角分别相等,则这个四边形是平行四边形.
(3)若两个三角形的三边成比例,则这两个三角形相似;
(1)若x=1,则x2=1;
(1)、(3)、(4)
若 ,则这个四边形是平行四边形.
2.请在横线上填写“四边形是平行四边形”的一个充分条件.
这样的充分条件唯一吗?
一般地,数学中的每一条判定定理都给出了相应数学结论的一个充分条件.
3.下列“若p,则q”形式的命题中,哪些q是p的必要条件?
(1)若x>1,则x>2;
(3)若四边形为矩形,则四边形为正方形;
(4)若四边形为菱形,则这个四边形的对角线互相垂直;
(2)若a=b,则ac=bc;
判断q是不是p的必要条件就是判断p是不是q的充分条件
若平面内两直线平行,则 .
4.请在横线上填写“平面内两直线平行”的一个必要条件.
这样的必要条件唯一吗?
一般地,数学中的每一条性质定理都给出了相应数学结论的一个必要条件.
(1)ab=0 a=0;
(4)ab>0 a>0,且b>0;
(5)四边形对角线互相垂直 四边形是菱形;
(6)圆C上存在点到直线l的距离等于半径 直线l与圆C相切;
核心素养 之 数据分析 + 逻辑推理
数或式之间的关系,可先对条件进行等价变形再判断;也可以结合函数图像来判断;几何条件的关系,往往借助于图形判断.
核心素养 之 数学抽象 + 数学建模
如图1,“x∈A” “x∈B”;“x∈A”是“x∈B”的 条件;
(用“充分”或“必要”填空)
如图2,“x∈P” “x∈Q”;“x∈P”是“x∈Q”的 条件;
当M⊆N时,“x∈M”是“x∈N”的 充分 条件; “x∈N”是“x∈M”的 必要 条件.
核心素养 之 数据分析 + 逻辑推理
(2)已知p:x-a>0, q:x>1. 若p是q的充分条件,则实 数的取值范围是 ; (3)已知A={x|a+1≤x≤2a+3}, B={x|-1≤x≤4},若x∈A 是x∈B的充分条件,则实数a的取值范围是 ;
2.(1)已知A是数集,则“A∩{0,1}={0}”是“A={0}” 的 条件;
(填“充分”或“必要”)
(B) p:x=1是方程ax2+bx+c=0的一个根; q:a+b+c=0.
(A) p:关于x 的方程ax2+bx+c=0有两个不相等的实数根; q:ac<0.
3.下列各选项中,p是q的充分但非必要条件的是( )
(C) p:平面内点P在线段AB的垂直平分线上; q:PA=PB.
核心素养 之 数学运算 + 逻辑推理
如果条件比较隐晦,可以先进行等价变形,然后再进行判断;比如 (A)中p: b2-4ac>0; (D)中p: x=2,q:x=2或-1
当有多个条件同时出现,关系比较复杂时,可以用“推出”或“推不出”将它们之间充分或必要的关系翻译成符号语言,然后依符号语言进行逻辑推理,得到目标之间的逻辑关系.
(1)若p是q的充分条件,q是r的充分条件,则r是p的 条件;
(2)若p是q的必要条件,r是q的充分条件,则r是p的 条件.
4. 用“充分”或“必要”填空:
(1) 由已知,有p→q,q→r; 从而p→r,故r是p的必要条件; (2) 由已知,有q→p,r→q; 从而r→p,故r是p的充分条件.
(2)“x+y=7”是“x2-y2-6x+8y=7”的 条件;
(3)“a>b-1”是“a3>b3”的 条件;
1. 用“充分”或“必要”填空:
数学思想 之 转化与化归
(4)“a2+b2+c2>ab+ac+bc”是“△ABC是直角三角形”的 条件(a,b,c是△ABC的三条边).
(1)充分;(先分子有理化) (2)充分;(先分组配方) (3)必要;(先因式分解) (4)必要;(先分组配方).
条件隐晦时,先要进行等价变形;常用的化归方法有:分子或分母有理化、通分、因式分解、配方等等 .
1)“a>b”是“a2>b2”的 条件;
(2)用“充分”、“必要”、“即充分又必要”或“即不充分又 不必要”当中的一个填空:
2)“a>b”是“ac2>bc2”的 条件;
2.(1)下面四个条件中,使a>b成立的一个必要条件是( )
数学思想 之 转化与化归 + 数形结合
判断变量之间的关系时,可借助于数轴、坐标系或函数图像;也可以根据特殊数字的特性作直观判断.
(1)D; (2) 1)即不充分又不必要;2)必要 3)必要 4) 即不充分又不必要
3. 以下选项中,既是“关于x的方程x2+2x-a=0有实数根”的充分条件,又是“关于x的方程x2+4x+2a=0无实数根”的必要条件的是( )
(A)a≥-2 (B)a≥0 (C) a≥2 (D) a≥4
数学思想 之 函数与方程思想
“关于x的方程x2+2x-a=0有实数根”的充分条件:{a|a≥-1}的子集;“关于x的方程x2+4x+2a=0无实数根”的必要条件:包含{a|a≥2}的集合;故选B
同时满足多个条件的,要先确定各个条件对应的参数范围,再结合数轴作出判断.
一、本节课学习的新知识
二、本节课提升的核心素养
三、本节课训练的数学思想方法
基础作业: .
能力作业: .
人教A版 (2019)必修 第一册3.2 函数的基本性质备课课件ppt: 这是一份人教A版 (2019)必修 第一册<a href="/sx/tb_c4000268_t3/?tag_id=26" target="_blank">3.2 函数的基本性质备课课件ppt</a>,共25页。PPT课件主要包含了符号表达,偶函数,奇函数,称yx为奇函数,练一练,答案t1,数形结合,分类讨论,转化与化归,课堂小结等内容,欢迎下载使用。
人教A版 (2019)必修 第一册5.3 诱导公式备课ppt课件: 这是一份人教A版 (2019)必修 第一册<a href="/sx/tb_c4000282_t3/?tag_id=26" target="_blank">5.3 诱导公式备课ppt课件</a>,共27页。PPT课件主要包含了复习回顾,诱导公式,α的终边,由三角函数的定义得,诱导公式二,诱导公式三,诱导公式四,公式二,公式三,公式四等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册4.3 对数备课ppt课件: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4000275_t3/?tag_id=26" target="_blank">4.3 对数备课ppt课件</a>,共30页。PPT课件主要包含了你注意到了什么,练一练,求下列各式的值,例题与练习,课堂小结,对数的运算,降次公式,逻辑推理,数学建模,数学运算等内容,欢迎下载使用。













