

初中数学人教版(2024)九年级上册22.1.1 二次函数达标测试
展开学习目标:
会用描点法画出二次函数 y=a(x-h)²的图像,并结合图像理解抛物线、对称轴、顶点坐标及开口方向等概念;
掌握二次函数 y=a(x-h)²性质,掌握y=ax²(a≠0)与y=a(x-h)²(a≠0)之间联系。
老师告诉你
根据图像的位置变换确定函数解析式时要注意:
平移(上下或左右)a不变,绕顶点旋转180°(沿x轴翻折)a变成原数的相反数。
一、知识点拨
1.知识导航
2.知识点梳理
知识点1 二次函数y=a(x-h)²的图像
a>0 ,开口向上 a<0,开口向下;
对称轴是直线x=h,顶点坐标(h,k)
二次函数y=a(x-h)2的图象可以由y=ax2的图象平移得到:
当h > 0 时,向右平移h个单位长度得到.当h < 0 时,向左平移-h个单位长度得到.
【新知导学】
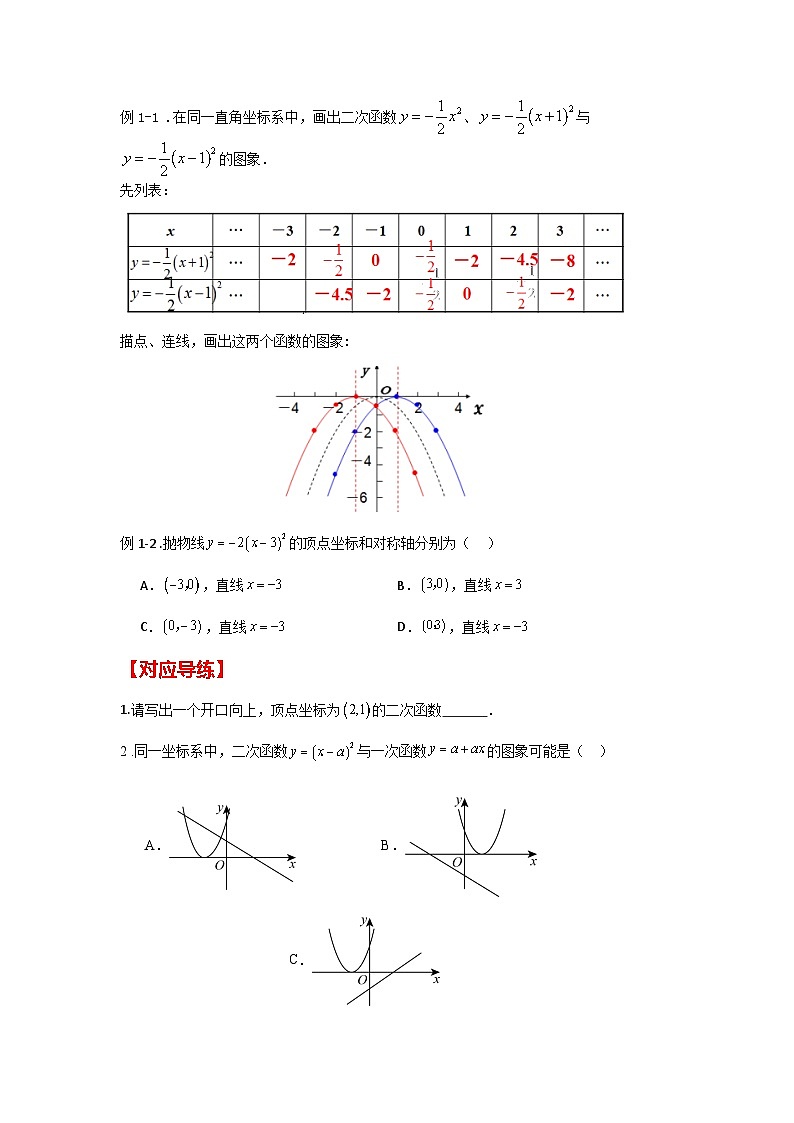
例1-1 .在同一直角坐标系中,画出二次函数、与的图象.
先列表:
描点、连线,画出这两个函数的图象:
例1-2 .抛物线的顶点坐标和对称轴分别为( )
A.,直线B.,直线
C.,直线D.,直线
【对应导练】
1.请写出一个开口向上,顶点坐标为的二次函数 .
2 .同一坐标系中,二次函数与一次函数的图象可能是( )
A. B. C. D.
知识点2 二次函数y=a(x-h)²的性质
【新知导学】
例2-1 .对于二次函数的图象,下列说法不正确的是( )
A.开口向上B.对称轴是直线
C.顶点坐标为D.当时,随的增大而增大
例2-2 .已知二次函数,如果函数值随自变量的增大而减小,那么的取值范围是( )
A.B.C.D.
【对应导练】
1.上,当时,随的增大而增大,则的取值范围是( )
A.B.C.D.
2 .抛物线的图象经过点,,,则,,大小关系是( )
A.B.C.D.
3 .二次函数的最大值是( )
A.B.0C.2D.3
知识点3 二次函数y=a(x-h)²与y=ax2 的平移关系
二次函数y=a(x-h)2的图象可以由y=ax2的图象平移得到:
当h > 0 时,向右平移h个单位长度得到.当h < 0 时,向左平移-h个单位长度得到.
左右平移规律:括号内左加右减;括号外不变
【新知导学】
例3-1 .抛物线与抛物线的关系:
若h>0,抛物线向 平移h个单位就得到抛物线;
若h<0,,抛物线向 平移|h|个单位就得到抛物线
例3-2 .抛物线y=3(x-2)2的开口方向是 ,顶点坐标为 ,对称轴是 .当x 时,y随x的增大而增大;当x= 时,y有最 值是 ,它可以由抛物线y=3x2向 平移 个单位得到.
【对应导练】
1.关于二次函数的图象,下列说法正确的是( )
A.开口向上B.最低点是
C.可以由向左平移2个单位得到D.当时,随的增大而增大
2.在平面直角坐标系中,将抛物线y=﹣2(x﹣1)2+3向下平移2个单位后所得抛物线的表达式为( )
A.y=﹣2(x+1)2+3B.y=﹣2(x﹣3)2+3
C.y=﹣2(x﹣1)2+5D.y=﹣2(x﹣1)2+1
3 .请在同一坐标系中画出二次函数①;②的图象.说出两条抛物线的位置关系,指出②的开口方向、对称轴和顶点.
题型训练
1.利用二次函数y=a(x-h)²的性质求最值
1.已知二次函数(h为常数),当自变量x满足时,其对应函数y的最大值为,则h的值为 .
2.如图,已知二次函数的图象顶点在轴上,且,与一次函数的图象交于轴上一点和另一交点.
求抛物线的解析式;
点为线段上一点,过点作轴,垂足为,交抛物线于点,请求出线段的最大值.
2.利用二次函数y=a(x-h)²的性质求面积
3.如图,抛物线y=2(x-2)2与平行于x轴的直线交于点A,B,抛物线顶点为C,△ABC为等边三角形,求S△ABC;
4 .如图1,E是等边△ABC的边BC上一点(不与点B,C重合),连接AE,以AE为边向右作等边△AEF,连接CF.已知△ECF的面积(S)与BE的长(x)之间的函数关系如图2所示(P为抛物线的顶点).
(1)当△ECF的面积最大时,∠FEC的大小为 .
(2)等边△ABC的边长为 .
5 .如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题:
(1)抛物线与x轴的一个交点A的坐标是 ,则抛物线与x轴的另一个交点B的坐标是 ;
(2)确定a的值;
(3)设抛物线的顶点是P,试求△PAB的面积.
利用二次函数y=a(x-h)²的图像确定位置变换
6.对于二次函数.
它的图象与二次函数的图象有什么关系?它是轴对称图形吗?它的开口方向,对称轴和顶点坐标分别是什么?
当取哪些值时,的值随的增大而增大?当取哪些值时,的值随的增大而减小?
7.如图,将抛物线C1:y=x2向右平移2个单位后,再将该图象关于x轴进行轴对称变换得到抛物线C2:y=ax2+bx+c.则下列关于抛物线C2的解析式中,正确的是( )
A.y=﹣x2+4x﹣4B.y=﹣x2﹣4x﹣4
C.y=x2+4x﹣4D.y=x2﹣4x﹣4
8.将抛物线y=ax2向右平移2个单位后所得抛物线与y轴交于点A(0,4).
(1)求平移后所得抛物线的解析式;
(2)平移后所得抛物线的对称轴上有一点P,要使PA+PO最短,求P点的坐标.
三、牛刀小试
选择题(共8小题,每小题4分,共32分)
1.顶点为且开口方向、形状与函数的图象相同的抛物线是( )
A.B.
C.D.
2 .对于二次函数,下列结论正确的是( )
A.y随x的增大而增大B.当时,y随x的增大而增大
C.当时,y随x的增大而增大D.当时,y随x的增大而增大
3.若、、为二次函数的图象上的三点,则、、的大小关系是( )
A.B.C.D.
4.已知,设函数,,.直线的图象与函数,,的图象分别交于点,,,下列说法正确的是( )
A.若,则B.若,则
C.若,则D.若,则
5 .关于x的二次函数与的性质中,下列说法错误的是( )
A.开口方向相同
B.对称轴相同
C.开口大小相同
D.当时,随x的增大而减小,随x的增大而增大
6 .已知点在抛物线上,且,则的取值范围是 .
7 .抛物线与抛物线的相同点是( )
A.开口方向相同B.对称轴相同C.形状大小都相同D.顶点都在轴上
8 .如图,在平面直角坐标系中,抛物线y=x−12与x轴只有一个交点M,与平行于x轴的直线l交于点A、B,若AB=4,则点M到直线l的距离为( )
A.2B.3C.4D.5
二、填空题(每小题4分,共20分)
9 .如果抛物线y=(a+2)x2+a的开口向下,那么a的取值范围是 .
10 .二次函数y=ax−ℎ2的图象如图所示,若A−2,y1,B−4,y2是该图象上的两点,则y1 y2.(填“>”“<”或“=”)
11 .已知二次函数y=−(x−ℎ)2(ℎ为常数),当2⩽x⩽5时,y的最大值为−1,则ℎ的值为 .
12 .在平面直角坐标系内有线段PQ,已知P(3,1)、Q(9,1),若抛物线与线段PQ有交点,则a 的取值范围是______.
13 .已知二次函数y=(x-m)2,当x≤1时,y随x的增大而减小,则m的取值范围是 .
三、解答题(共6小题,共48分)
14 .(8分)如图是二次函数的图象,,试求该抛物线的解析式.
15 .(6分)已知二次函数y=2x−12的图象如图所示,求△ABO的面积.
16 .(8分)抛物线的顶点为,它的形状与相同,但开口方向与之相反.
(1)直接写出抛物线的解析式 ;
(2)求抛物线与轴的交点坐标.
17 .(8分)已知二次函数.
(1)画出函数图象,确定抛物线的开口方向、顶点坐标和对称轴.
(2)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小?
18 .(9分)如图,已知抛物线的顶点A的坐标为,经过点A的直线交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.
(1)求这条抛物线对应的函数解析式;
(2)求直线AB对应的函数解析式;
(3)若点D在x轴上,且是等腰三角形,请直接写出D点的坐标.
19 .(9分)已知点是抛物线上的点,且点P在第一象限内.
(1)求m的值;
(2)过P点作轴交抛物线于点Q,若a的值为3,试求以P点、Q点及原点O为顶点的三角形的面积y=a(x-h)2
a>0
a<0
开口方向
开口向上
开口向下
顶点坐标
(h,0)
(h,0)
最值
当x= h时,y取最小值0
当x= h时,y取最大值0
对称轴
直线x=h
直线x=h
增减性
当x<h时,y随x的增大而减小;当x>h时,y随x的增大而增大。
当x<h时,y随x的增大而增大;当x>h时,y随x的减小而减小。
人教版(2024)九年级上册22.1.1 二次函数一课一练: 这是一份人教版(2024)九年级上册<a href="/sx/tb_c95446_t7/?tag_id=28" target="_blank">22.1.1 二次函数一课一练</a>,共40页。试卷主要包含了知识点拨,牛刀小试,填空题等内容,欢迎下载使用。
人教版九年级上册22.1.3 二次函数y=a(x-h)2+k的图象和性质优秀练习题: 这是一份人教版九年级上册22.1.3 二次函数y=a(x-h)2+k的图象和性质优秀练习题,文件包含第10课二次函数yax2与yax-h2+k的图像与性质教师版docx、第10课二次函数yax2与yax-h2+k的图像与性质学生版docx等2份试卷配套教学资源,其中试卷共40页, 欢迎下载使用。
初中数学人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.3 二次函数y=a(x-h)2+k的图象和性质课后练习题: 这是一份初中数学人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.3 二次函数y=a(x-h)2+k的图象和性质课后练习题,共17页。













