初中数学北师大版（2024）八年级下册第三章图形的平移与旋转1 图形的平移同步达标检测题

展开

这是一份初中数学北师大版（2024）八年级下册第三章图形的平移与旋转1 图形的平移同步达标检测题，共30页。

2．如图，D是内一点，，，，，，则的长是_____________．
3．如图，为等边三角形，点P为内一点，且，，，M、N为、上的动点，且，则的最小值为__________．
4．如图所示，，点是轴上一个动点，将线段绕点顺时针旋转得到线段，连接．则线段的最小值是__________．
5．如图，直线l上依次有，，，四点，且，以为边作等边，连接，；若，，则的长是______．
6．如图，在中，，，P为内一点，且，，，则的面积为______．
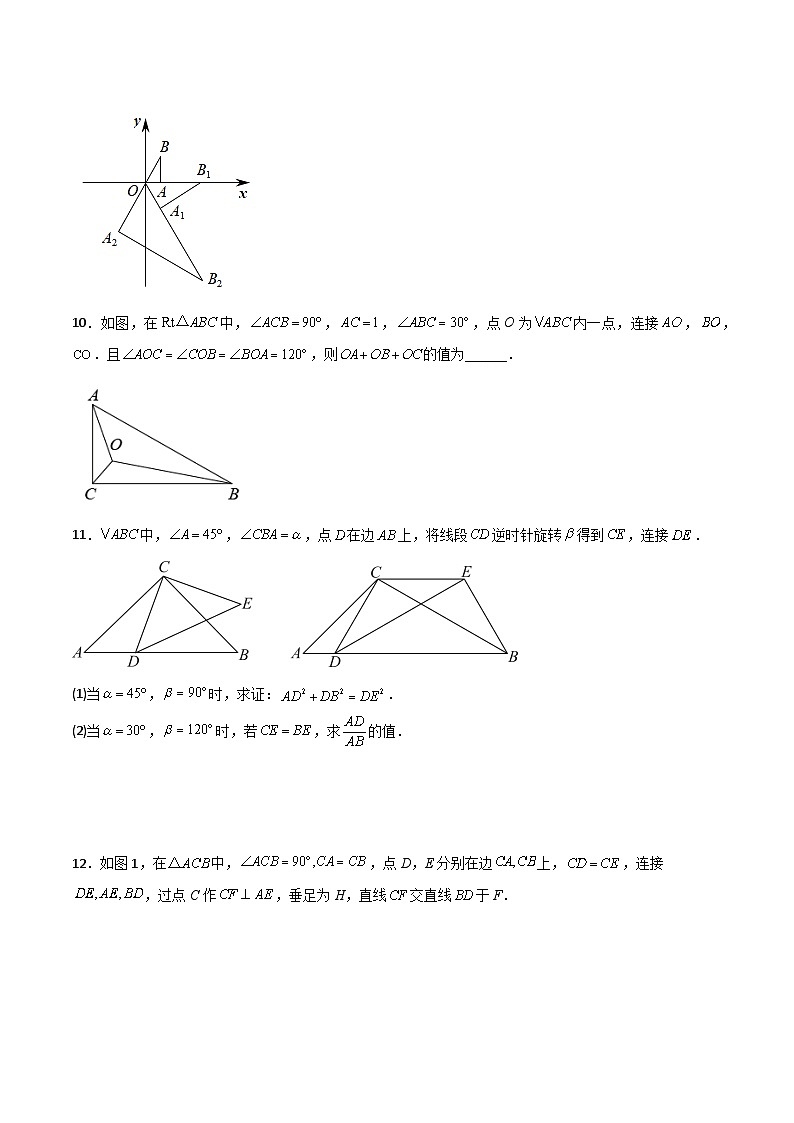
7．如图，在平面直角坐标系中，将绕点A顺时针旋转到的位置，点B，O分别落在点，处，点在x轴上，再将绕点顺时针旋转到的位置，点在x轴上，再将绕点顺时针旋转到的位置，点在x轴上，依次进行下去，…，若点，，，则点的坐标为______．
8．如图，含角的直角三角形纸片将该纸片在平面直角坐标系中放置，将该纸片绕着原点按顺时针方向旋转得到，连结，，分别为，的中点，若，则直线与轴的交点坐标为___________．
9．如图，在平面直角坐标系中，点的坐标分别为，，将绕原点顺时针旋转，再将其各边都扩大为原来的2倍，使得，，得到；将绕原点顺时针旋转，再将其各边都扩大为原来的2倍，使得，，得到……如此继续下去，得到，则点的坐标是______．
10．如图，在中，，，，点O为内一点，连接，，．且，则的值为______．
11．中，，，点在边上，将线段逆时针旋转得到，连接．
(1)当，时，求证：．
(2)当，时，若，求的值．
12．如图1，在中，，点D，E分别在边上，，连接，过点C作，垂足为H，直线交直线于F．
(1)求证：；
(2)将图1中的绕点C逆时针旋转，其他条件不变，如图2，（1）的结论是否成立？如果成立，请证明：如果不成立，请说明理由；
(3)若，将绕点C逆时针旋转一周，当A，E，D三点共线时，直接写出的长．
13．(1)发现：如图，点是线段上的一点，分别以，为边向外作等边三角形和等边三角形，连接，，相交于点．
①线段与的数量关系为：；的度数为．
②可看作经过怎样的变换得到的？．
(2)应用：如图2，若点，，不在一条直线上，中的结论①还成立吗？请说明理由；
(3)拓展：在四边形中，，，，若，，请直接写出，两点之间的距离．
14．在中，，点D是边上一动点，连接．将线段绕着D逆时针旋转得到，连接．
(1)当时，
①如图1，若，，求的长：
②如图2，过点C作于F，当点D在线段上时，过点E作交于点G．求证：；
(2)如图3，若，，请直接写出的最小值．
15．在中于点．
(1)如图1，若的角平分线交于点，，，求的度数；
(2)如图2，点、分别在线段、上，将折叠，点落在点处，点落在点处，折痕分别为和，点、均在直线上，若，试猜想与之间的数量关系，并简要说明理由；
(3)在（2）小题的条件下，将绕点逆时针旋转一个角度，记旋转中的为（如图3）．在旋转过程中，直线与直线交于点，与直线交于点．若，是否存在这样的、两点，使为直角三角形？若存在，请直接写出旋转角的度数；若不存在，请说明理由．
第三章图形的平移与旋转B卷压轴题考点训练
1．如图，点，，作点关于轴的对称点，若点是直线上的动点，连，将绕点逆时针旋转至，则的最小值是_____．
【答案】
【详解】解：如图所示，过点分别作轴的垂线，垂足分别为，
∵将绕点逆时针旋转至，
则，
∵，，
∴，
∴，
∴，
∵，，
设直线的解析式为，
∴，
解得：
∴直线的解析式为，
∵点是直线上的动点，
∵关于轴对称，
∴,
如图所示，
设，则，，
∴，
∴，
∵，
∴点在直线上运动，
设直线与坐标轴的交点为，则是等腰直角三角形，
∴,,
∵是等腰直角三角形，
∴，
作关于的对称点，则是等腰直角三角形（），
∴，
∴
∴，
∴当三点共线时，最小，最小值为的长，
即，
故答案为：．
2．如图，D是内一点，，，，，，则的长是_____________．
【答案】
【详解】解：将绕点D顺时针旋转至，连接，交于F，交于M，
则，，
，
，
又，，
，
，，
，
，
，
在与中，
，
，
，
，解得：
，
，
在中，，
故答案为：．
3．如图，为等边三角形，点P为内一点，且，，，M、N为、上的动点，且，则的最小值为__________．
【答案】
【详解】解：如图1，将绕点顺时针旋转得到，连接、，则，，
，，
是等边三角形，，，
，
，
，
如图2，将绕点逆时针旋转得到，连接、，则，，
，，
是等边三角形，，
，
，
则的最小值为，
故答案为．
4．如图所示，，点是轴上一个动点，将线段绕点顺时针旋转得到线段，连接．则线段的最小值是__________．
【答案】2
【详解】解：连接，以为边长作等边，连接，
，，
，，
为等边三角形，
，，
，
在和中，
，，，
当点在轴上运动时，点在直线上运动，
作交直线于，于，
，，
，，，
显然，当在直线上运动到点位置时，线段的最小值为，
故答案为：2．
5．如图，直线l上依次有，，，四点，且，以为边作等边，连接，；若，，则的长是______．
【答案】
【详解】解：设则
为等边三角形，
，，
，
把绕点顺时针旋转得到，
，，，
，
，
在和中，
，
，
，
，，
，
过点作于，如图，
，
点与点重合，即，
在中，，
即，
．
故答案为．
6．如图，在中，，，P为内一点，且，，，则的面积为______．
【答案】
【详解】解：如图，
把绕点逆时针旋转90°得到，
根据旋转的性质可得是等腰直角三角形，
，，
，

，

在直角三角形中
故答案为：．
7．如图，在平面直角坐标系中，将绕点A顺时针旋转到的位置，点B，O分别落在点，处，点在x轴上，再将绕点顺时针旋转到的位置，点在x轴上，再将绕点顺时针旋转到的位置，点在x轴上，依次进行下去，…，若点，，，则点的坐标为______．
【答案】
【详解】∵，，
∴，，
∵，
∴，
∴的横坐标为：12，且，
∴的横坐标为：，
…，
∴的横坐标为：，
∵，
∴点的横坐标为：，
∵，
∴点的纵坐标为4，
∴．
故答案为：．
8．如图，含角的直角三角形纸片将该纸片在平面直角坐标系中放置，将该纸片绕着原点按顺时针方向旋转得到，连结，，分别为，的中点，若，则直线与轴的交点坐标为___________．
【答案】
【详解】解：在中，，，，
，点的坐标为，
，
点的坐标为，．
由旋转的性质可知：，，，
点的坐标为，为等边三角形．
点为线段的中点，
点的坐标为．
过点作轴于点，如图所示，
为等边三角形，
，
，
点的坐标为．
点为线段的中点，
点的坐标为，．
设直线的解析式为，
将，，代入得：，解得：，
直线的解析式为．
当时，，
直线与轴的交点坐标为．
故答案为：．
9．如图，在平面直角坐标系中，点的坐标分别为，，将绕原点顺时针旋转，再将其各边都扩大为原来的2倍，使得，，得到；将绕原点顺时针旋转，再将其各边都扩大为原来的2倍，使得，，得到……如此继续下去，得到，则点的坐标是______．
【答案】
【详解】解：如图所示：
，，
，，轴，
，
，
每一次旋转角是，
旋转次后，正好旋转一周，点在轴的正半轴上，
，
点与点在同一条射线上，如图所示，
每次旋转后，，，，
，，，
依此类推，，
当时，，根据含锐角的直角三角形的三边关系可知点的坐标是，即，
故答案为：．
10．如图，在中，，，，点O为内一点，连接，，．且，则的值为______．
【答案】
【详解】解：∵，，，
∴，．
如图，将绕点B顺时针方向旋转得到，
∴，，
∵，，∴是等边三角形，
∴，，
∵ ，
∴ ，∴ 四点共线，
在中，，
∴．故答案为：．
11．中，，，点在边上，将线段逆时针旋转得到，连接．
(1)当，时，求证：．
(2)当，时，若，求的值．
【答案】(1)证明见解析
(2)
【详解】（1）证明：如图，连接，
，
，
在和中，
，
，
，，
，
，
，
；
（2）在的延长线上取点，使
，
由同理得，
，
，
设，
∴
作于，
，
是等腰直角三角形，
∴．
12．如图1，在中，，点D，E分别在边上，，连接，过点C作，垂足为H，直线交直线于F．
(1)求证：；
(2)将图1中的绕点C逆时针旋转，其他条件不变，如图2，（1）的结论是否成立？如果成立，请证明：如果不成立，请说明理由；
(3)若，将绕点C逆时针旋转一周，当A，E，D三点共线时，直接写出的长．
【答案】(1)见解析
(2)仍然成立，理由见解析
(3)
【详解】（1）证明：在和中，
，
∴，
∴，
∵，
∴，
又∵，
∴，
∴，
∴，
∵，，，
∴，
∴，
∴；
（2）仍然成立，理由如下：
如下图，作交直线于点，
∴，
又∵，
∴，
又∵，
∴，
∴，
又∵，
∴，
又∵，
∴，
∴，
又∵，
∴，
又∵，
∴，
∴，
∴；
（3）解：①当点在延长线上时，过点作于点，如下图，
∵，
∴，
∵，
∴，
∵，
∴，
∴，
由（2）可知，，
又∵，
∴，
∴，
∴，
∴；
②当点在线段上时，过点作于点，如下图，
同理可得，，，
∴，
∴．
综上所述，的长为或．
13．(1)发现：如图，点是线段上的一点，分别以，为边向外作等边三角形和等边三角形，连接，，相交于点．
①线段与的数量关系为：；的度数为．
②可看作经过怎样的变换得到的？．
(2)应用：如图2，若点，，不在一条直线上，中的结论①还成立吗？请说明理由；
(3)拓展：在四边形中，，，，若，，请直接写出，两点之间的距离．
【答案】(1)①，；②可看作绕点顺时针旋转得到的；(2)(1)中的结论①依然成立；理由见解析；(3)
【详解】解：（1）①、都为等边三角形，
，，，
，
在和中，，
，
，，
，
，
故答案为：，；
②由①知：，
，，，
，
可看作绕点顺时针旋转得到的，
故答案为：可看作绕点顺时针旋转得到的；
（2）若点，，不在一条直线上，（1）中的结论①依然成立；理由如下：
、都为等边三角形，
，，，
，
在和中，，
，
，，
，
；
（3）过点作于，过点作，交延长线于，如图所示：
，是等腰直角三角形，
，，
，，
在和中，，
，
，
，
．
14．在中，，点D是边上一动点，连接．将线段绕着D逆时针旋转得到，连接．
(1)当时，
①如图1，若，，求的长：
②如图2，过点C作于F，当点D在线段上时，过点E作交于点G．求证：；
(2)如图3，若，，请直接写出的最小值．
【答案】(1)①②证明见解析；(2)3
【详解】（1）①解：过点C作于F，
∵，，
∴，，
在中，
由勾股定理得，，
∵，，
∴，
解得：，
∵
∴，
在中，
由勾股定理得，，
即
解得：，
∵，，
∴，
∴；
②过点E作于H，
∵，，
∴，
∵，
∴，
在和中，

∴，
∴，
∵，
∴，
∵，
∴，
∴，
∵，
∴，
∴，即，
∵，
∴，
∴，
∵，
∴，
∴，
∵，
∴，即；
（2）如图，过点C作于点F，以点B为顶点在上方作，
过点D作于点M，过点C作于点N，
点D是上的动点，运动到某一时间有，
此时，，
∵，
∴，，
∵，，
∴，，
设的长为x，则，
∵∠，
∴，
∴，
在中，由勾股定理得，，
，
即，
解得：，
∴，，
在中，，
∵，，
∴，
∵是由旋转得到，
∴，
∴即为，
最小时，即最小，
当C、D、M三点共线时最小，即图中的，
，
∵，
∴，，
∴为等腰直角三角形，
∴，
∵，
∴，
∵，
∴，
∴，
即的最小值为3．
15．在中于点．
(1)如图1，若的角平分线交于点，，，求的度数；
(2)如图2，点、分别在线段、上，将折叠，点落在点处，点落在点处，折痕分别为和，点、均在直线上，若，试猜想与之间的数量关系，并简要说明理由；
(3)在（2）小题的条件下，将绕点逆时针旋转一个角度，记旋转中的为（如图3）．在旋转过程中，直线与直线交于点，与直线交于点．若，是否存在这样的、两点，使为直角三角形？若存在，请直接写出旋转角的度数；若不存在，请说明理由．
【答案】(1)
(2)，理由见解析
(3)存在，旋转角的度数为或，理由见解析
【详解】（1）解：如图，
∵，
∴，
又∵，
∴，
∵，
∴，
又∵平分，
∴，
∴，
∴．
∴的度数为．
（2）结论：．
理由：如图，
由翻折可知，，
∵，，
∴，
∴，
∵，
∴，
即，
∴．
（3）①当时，
∴，
∵将折叠，点落在点处，折痕为，将绕点逆时针旋转一个角度，
∴，
∴，
∴，
∴；
②当时，
∵将折叠，点落在点处，折痕为，将绕点逆时针旋转一个角度，
∴，
∴，
∵，
∴，
∴，
∴．
综上所述，旋转角的度数为或．