北师大版数学八年级下册 第三章《图形的平移与旋转》单元小结 课件+单元测试（含答案解析）

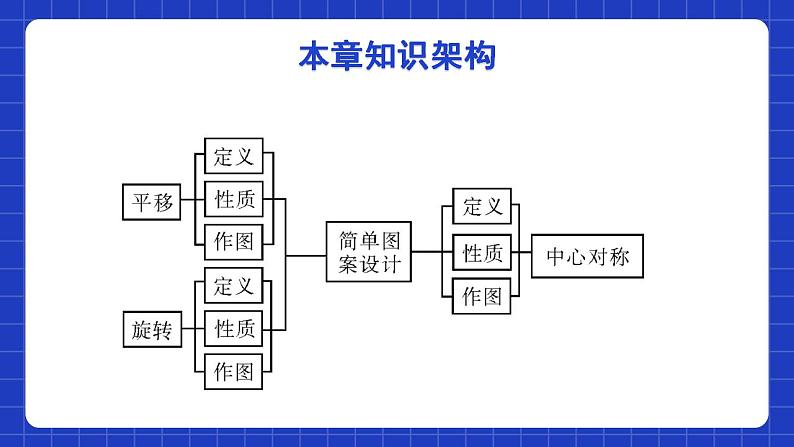
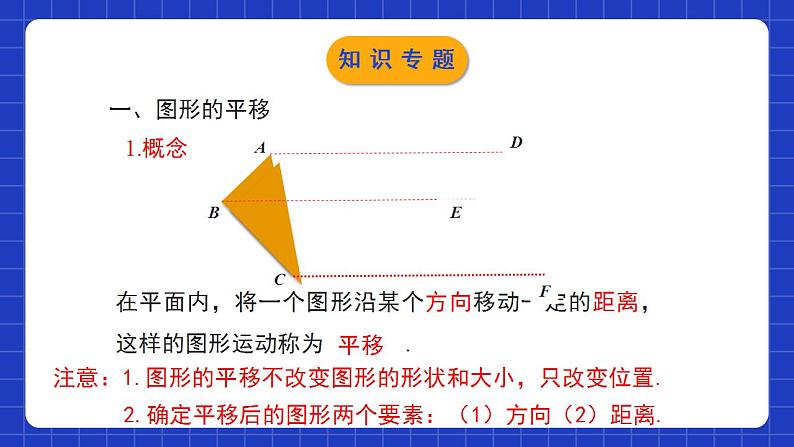
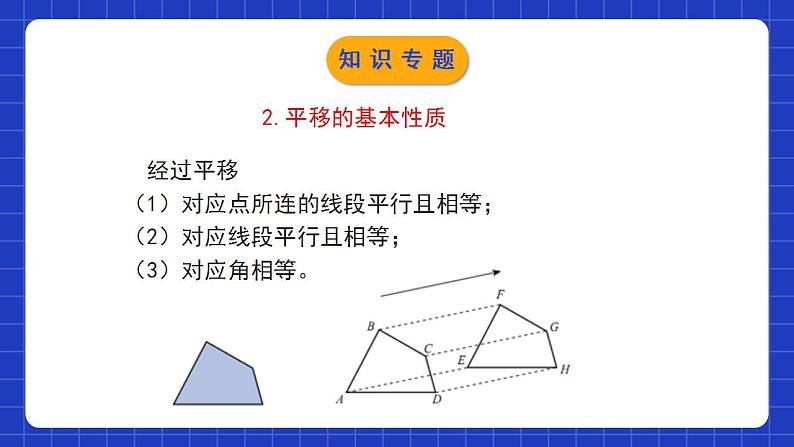
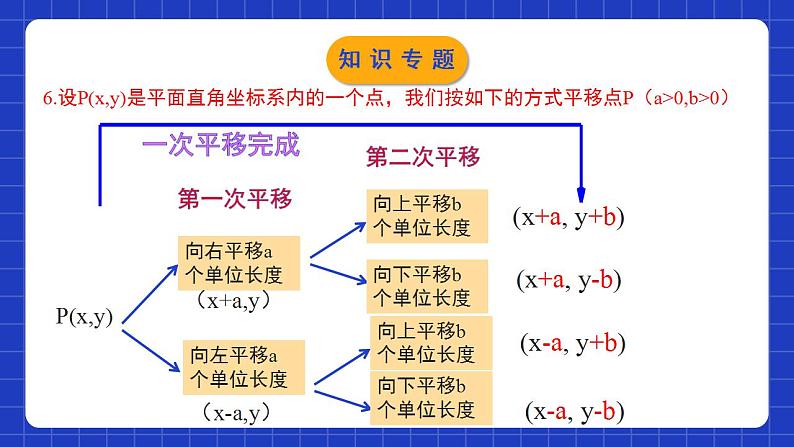
第三章图形的平移与旋转单元小结本章知识架构本章知识架构一、图形的平移1.概念在平面内，将一个图形沿某个方向移动一定的距离，这样的图形运动称为 .平移注意：1.图形的平移不改变图形的形状和大小，只改变位置.ABC2.确定平移后的图形两个要素：（1）方向（2）距离.知识专题2.平移的基本性质 经过平移（1）对应点所连的线段平行且相等；（2）对应线段平行且相等；（3）对应角相等。知识专题3.平移作图的一般步骤：应分四步——定、找、移、连．(1)定：确定平移的方向和距离；(2)找：找出表示图形的关键点(图形的顶点、拐点、连接点)；(3)移：过关键点作平行且相等的线段，得到关键点的对应点；（平行和相等可以按照平移方向和距离，也可以按照对应边的关系）(4)连：按原图顺次连接对应点．知识专题4.图形平移后，各点坐标的变化规律 如果平移的单位是常量a(a＞0)，原坐标为(x，y)，图形平移后的对应点的坐标：①原图形向右(向左)平移a个单位长度：对应点的坐标为(x±a，y)②原图形向上(向下)平移a个单位长度：对应点的坐标为(x，y±a)知识专题 5.坐标变化后，图形的变化规律 ①横坐标保持不变，纵坐标分别加2，原图形被向上平移2个单位长度．②横坐标保持不变，纵坐标分别减2，原图形被向下平移2个单位长度．知识专题6.设P(x,y)是平面直角坐标系内的一个点，我们按如下的方式平移点P（a>0,b>0）P(x,y)(x+a, y+b)(x+a, y-b)(x-a, y+b)(x-a, y-b)（x+a,y）（x-a,y）知识专题7.设P(x,y)是平面直角坐标系内的一个点，我们按如下的方式平移点P（a>0,b>0）P(x,y)向右a个，向上b个单位长度向右a个，向下b个单位长度向左a个，向上b个单位长度向左a个，向下b个单位长度图形向右平移a个单位图形向左平移a个单位知识专题原图形上点P（x,y)平移后图形上点P（x±a,y±b)图形沿x轴方向平移a个单位长度图形沿y轴方向平移b个单位长度平移的方向：从原图形上一点到其对应点的方向.平移的距离：将一个图形沿着x轴方向平移a(a＞0）个单位长度；再严重y轴方向平移b个单位长度，平移前后图形对应点的坐标关系知识专题二、图形的旋转1.概念 在平面内，将一个图形绕一个定点按某个方向转动一个角度，这样的图形运动称旋转.这个定点称为旋转中心，转动的角称为旋转角。知识专题 旋转中心 旋转角 旋转方向 确定一次图形的旋转时,必须明确温馨提示：①旋转的范围是“平面内”; ②旋转变换同样属于全等变换.旋转三要素旋转不改变图形的形状和大小旋转角：是对应点与旋转中心所连线段的夹角知识专题2.旋转的性质（1）旋转不改变图形的大小和形状．（2）对应线段相等，对应角相等.（3）对应点到旋转中心的距离相等.（4）任意一组对应点与旋转中心的连线所成的角都等于旋转角.知识专题（1）确定旋转中心、旋转方向和旋转角；（2）将图形中的关键点与旋转中心连接起来，然后按旋转方向分别将它们旋转旋转角，截取相等线段得到关键点的对应点；（3）按照原图形的顺序连接这些对应点，所得到的图形就是旋转后的图形；（4）写出结论。3.画旋转图形的一般步骤：知识专题三、中心对称1.概念中心对称：如果把一个图形绕着某一点旋转180°，它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做它们的对称中心.中心对称的特征：①两个图形能够完全重合；②重合方式有限制：绕着某一点旋转180°.知识专题（1）成中心对称的两个图形中，对应点所连线段经过对称中心，且被对称中心平分.（即对称点与对称中心三点共线）（2）中心对称的两个图形是全等形. 2.中心对称的性质 知识专题 把一个图形绕某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心. 3.中心对称图形知识专题4.中心对称与中心对称图形的区别与联系：知识专题考点一 平移1.如图所示，△DEF经过平移得到△ABC，那么∠C的对应角和ED的对应边分别是 （ ）A.∠F，ACB.∠BOD，BAC.∠F，BAD.∠BOD，ACC 平移前后的图形形状和大小完全相同，任何一对对应点连线段平行（或共线）且相等.考点专练考点二 坐标系中的图形平移2.如图，在平面直角坐标系中，P（a，b）是△ABC的边AC上一点，△ABC经平移后点P的对应点为P1（a+6，b+2），（1）请画出上述平移后的△A1B1C1，并写出点A、C、A1、C1的坐标；（2）求出以A、C、A1、C1为顶点的四边形的面积．考点专练解：(1)△A1B1C1如图所示；各点的坐标为：A （﹣3，2）、C（﹣2，0）、A1（3，4）、C1（4，2）；(2)如图，连接AA1、CC1；△AC1C的面积                                △AC1A1的面积                                     四边形ACC1A1的面积为7+7=14.答：四边形ACC1A1的面积为14．考点专练考点三 旋转的概念及性质的应用3.如图，在等腰Rt△ABC中，点O是AB的中点，AC=4, 将一块边长足够大的三角板的直角顶点放在O点处，将三角板绕点O旋转，始终保持三角板的直角边与AC相交，交点为D,另一条直角边与BC相交，交点为E,则等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和等于 .4考点专练考点四 中心对称4.如图，矩形ABCD的对角线AC和BD相交于点O，过点O的直线分别交AD和BC于点E、F，AB＝2，BC＝3，则图中阴影部分的面积为_______.解析：由于矩形是中心对称图形，所以依题意可知△BOF与△DOE关于点O成中心对称，由此图中阴影部分的三个三角形就可以转化到直角△ADC中，易得阴影部分的面积为3．3考点专练课程结束