初中数学北师大版（2024）七年级上册（2024）1 代数式第1课时教案设计

这是一份初中数学北师大版（2024）七年级上册（2024）1 代数式第1课时教案设计，共5页。教案主要包含了情境引入，教学建议，对应训练，课堂总结，知识结构，作业布置等内容，欢迎下载使用。

第1课时 代数式
解题大招 根据实际问题列代数式（含代数式书写规范）
（1）根据实际问题写出代数式的方法：
①抓住关键性词语，如“大”“小”“多”“少”“和”“差”“商”“倍”等，弄清题目中的量及各个量之间的关系；
②厘清运算顺序，通常遵循“先读先写”的顺序列式。
（2）代数式的书写规范：
例1 下列代数式中，书写规范的是（ C ）
例2 填空：
（1）温度由t℃下降2℃后是 （t-2） ℃；
（2）如果手机通话的费用为每分钟m元，那么通话n min的费用为 mn 元；
（3）小明和小华都是集邮爱好者，已知小明收集了x张邮票，小华收集的邮票张数比小明收集的邮票张数的一半多5，则小华收集了张邮票。
培优点 用字母表示一般规律
例 用小棒按如图所示的规律拼摆图形：
（1）第4个图形中有 35 根小棒，第5个图形中有 43 根小棒。
（2）第n个图形中有多少根小棒？
分析：第1个图形中有11根小棒，第2个图形增加了两个六边形，增加的小棒的根数为8；第3个图形又增加了两个六边形，再增加8根小棒……
解：（1）35 43 【解析】观察图形，发现第1个图形有2个六边形，小棒的根数为11，后面的每个图形比前一个图形增加2个六边形，增加的小棒的根数为8。所以第2个图形中小棒的根数为11+8=19，第3个图形中小棒的根数为11+8×2=27，第4个图形中小棒的根数为11+8×3=35，第5个图形中小棒的根数为11+8×4=43。
（2）根据前面的分析，第n个图形中小棒的根数为11+8（n-1)。教学目标
课题
第1课时 代数式
授课人
素养目标
1.经历探索规律并用代数式表示规律的过程，感受从具体到抽象的思想。
2.能用字母表示运算律、计算公式以及一些简单问题中的数量关系和变化规律。
3.了解代数式的概念。
教学重点
用代数式表示规律、数量关系以及代数式的概念。
教学难点
探索规律的过程及用代数式表示规律的方法。
教学活动
教学步骤
师生活动
活动一：创设情
境，新课导入
设计意图
通过有趣的情境引入课题，激发学生学习兴趣。
【情境引入】
想一想，填一填：
兔子数量
嘴/张
耳朵/只
腿/条
1只
1
2
4
2只
2
4
8
3只
3
6
12
…
…
…
…
n只
n
2n
4n
由此看出n是一个字母，它代表“很多”的数量。用字母n可以清楚地表示出兔子数量和兔子的嘴、耳朵、腿之间的数量关系。
本节课我们一起来探寻这些式子的秘密。
【教学建议】
教学时，让学生自行说出兔子的数量与嘴的数量、耳朵数量和腿的数量的关系，初步体会代数式引入的必要性。
活动二：交流讨论，探究新知
设计意图
由特例归纳一般规律，并用字母表示一般规律，发展符号意识和抽象思维。
探究点 代数式
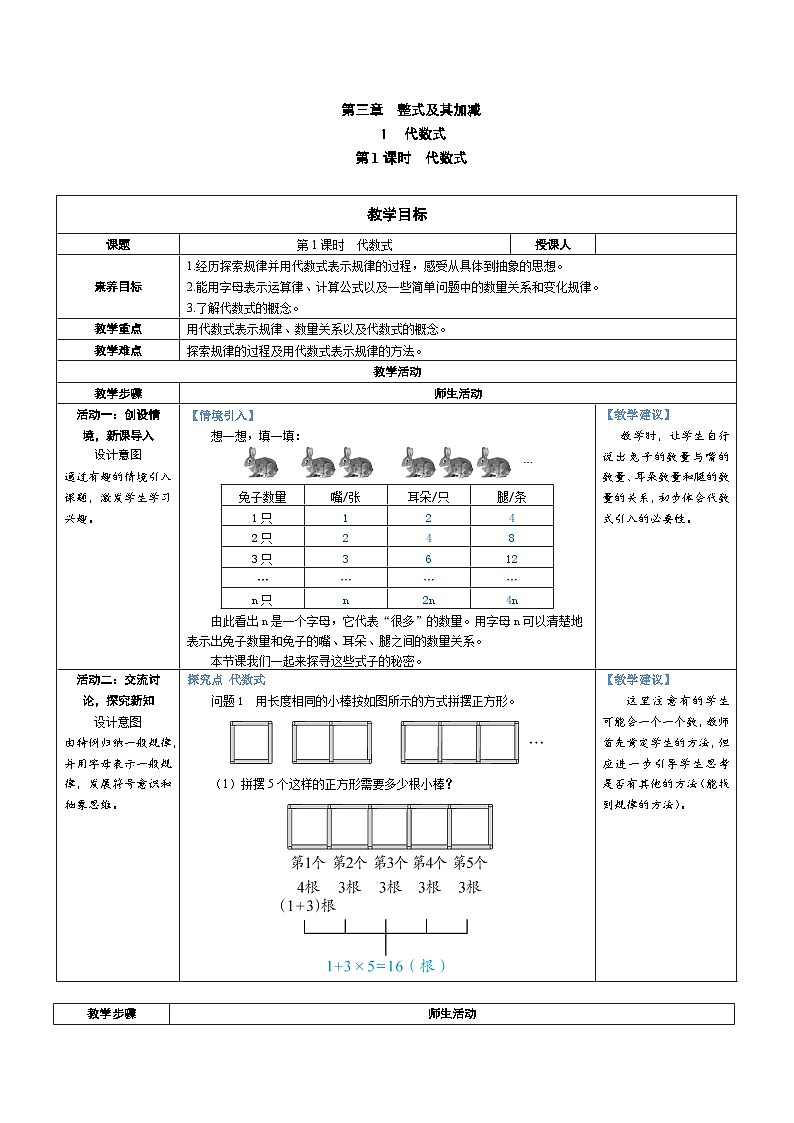
问题1 用长度相同的小棒按如图所示的方式拼摆正方形。
（1）拼摆5个这样的正方形需要多少根小棒？
【教学建议】
这里注意有的学生可能会一个一个数，教师首先肯定学生的方法，但应进一步引导学生思考是否有其他的方法（能找到规律的方法）。
教学步骤
师生活动
设计意图
启发学生体会字母表示数的优越性和广泛应用。
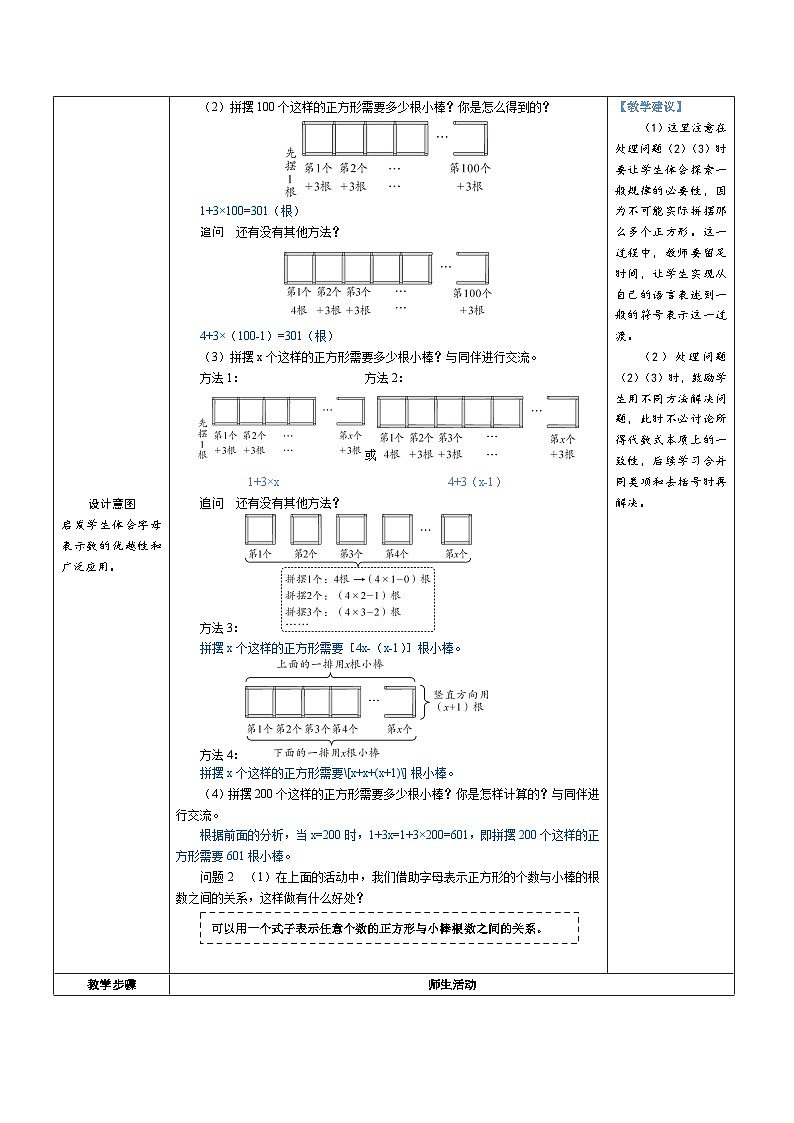
（2）拼摆100个这样的正方形需要多少根小棒？你是怎么得到的？
1+3×100=301（根）
追问 还有没有其他方法？
4+3×（100-1）=301（根）
（3）拼摆x个这样的正方形需要多少根小棒？与同伴进行交流。
方法1： 方法2：
或
1+3×x 4+3（x-1）
追问 还有没有其他方法？
方法3：
拼摆x个这样的正方形需要［4x-（x-1）］根小棒。
方法4：
拼摆x个这样的正方形需要\[x+x+(x+1)\]根小棒。
（4）拼摆200个这样的正方形需要多少根小棒？你是怎样计算的？与同伴进行交流。
根据前面的分析，当x=200时，1+3x=1+3×200=601，即拼摆200个这样的正方形需要601根小棒。
问题2 （1）在上面的活动中，我们借助字母表示正方形的个数与小棒的根数之间的关系，这样做有什么好处？
可以用一个式子表示任意个数的正方形与小棒根数之间的关系。
【教学建议】
（1）这里注意在处理问题（2）（3）时要让学生体会探索一般规律的必要性，因为不可能实际拼摆那么多个正方形。这一过程中，教师要留足时间，让学生实现从自己的语言表述到一般的符号表示这一过渡。
（2）处理问题（2）（3）时，鼓励学生用不同方法解决问题，此时不必讨论所得代数式本质上的一致性，后续学习合并同类项和去括号时再解决。
教学步骤
师生活动
设计意图
通过更多实际问题中的列式，引出代数式的概念。
（2）在以前的学习中还有哪些地方用到了字母？这些字母都表示什么？与同伴进行交流。
在一些运算律和计算公式中用到了字母。举例如下：
用字母表示数的运算律 用字母表示面积公式
运算定律
字母表示
加法交换律
ɑ+b=b+ɑ
加法结合律
（ɑ+b）+c=ɑ+（b+c）
乘法交换律
ɑb=bɑ
乘法结合律
（ɑb）c=ɑ（bc）
乘法对加法的分配律
ɑ(b+c)=ɑb+ɑc
问题3
（1）今年李华m岁，去年李华 (m-1) 岁，5年后李华 (m+5) 岁。
（2）ɑ个人n天完成一项工作，那么平均每人每天的工作量为。
（3）某商店上月的收入为ɑ元，本月的收入比上月收入的2倍还多10元，本月的收入是 (2ɑ+10) 元。
（4）如果一个正方体的棱长是ɑ-1，那么这个正方体的体积是 (ɑ－1)3 ，表面积是 6(ɑ－1)2 。
用具体数值代替代数式中的字母，就可以求出代数式的值。
【对应训练】
1.判断下列式子哪些是代数式，哪些不是代数式，是的打“√”，不是的打“×”。
2~3.教材P78随堂练习第1，2题。
【教学建议】
教师不要直接明晰结论，应先鼓励学生尽可能回忆以前学过的运算法则、运算律及计算公式等，写出相应的字母表示，并让学生说明其中每个字母代表的含义。
【教学建议】
在介绍代数式时，教师可以跟学生强调，代数式中的同样的字母在不同的问题中可以代表不同的量；在同一个问题中，不同的量要用不同的字母来表示。另外还要注意书写的一些规范（具体可参见备课素材）。
活动三：随堂训练，课堂总结
【课堂总结】师生一起回顾本节课所学主要内容，并请学生回答以下问题：
1.用字母表示数有什么好处？
2.什么是代数式？
【知识结构】
教学步骤
师生活动
【作业布置】
1.教材P82~87习题3.1第1，11，13题。
板书设计
1 代数式
第1课时 代数式
1.用代数式表示规律。 2.代数式的概念。
教学反思
探索正方形个数与小棒根数之间的关系，对学生来说比较有挑战性，学生一般难以系统性地总结一般规律，要鼓励学生多尝试，慢慢积累经验，提升这方面的能力。从用字母表示一般规律，进而拓展到用字母表示数的各种应用场景，以及了解代数式的概念，是本节课的主要目标。可让学生在今后的学习中，进一步体会用字母表示数带来的方便。
书写规范
举例
①数与字母相乘或字母与字母相乘，通常将乘号写作“·”或省略不写，数要写在字母的前面
10×m写成10·m或10m
x×y写成x·y或xy
②数字因数是“1”或“-1”时，常省略“1”
1ɑ写成ɑ，-1ɑb写成-ɑb
③数字因数是带分数时，要写成假分数
④含字母的除法运算中，结果要写成分数形式
⑤式子后面有单位且式子是和或差的形式时，应把式子用括号括起来
(2x+4y)kg