

- 2.2.2 有理数的除法 第1课时 有理数的除法(教学设计) --2024--2025学年人教版(2024)七年级数学上册 教案 3 次下载
- 2.2.2 有理数的除法 第2课时 有理数的加减乘除混合运算(教学设计) --2024--2025学年人教版(2024)七年级数学上册 教案 1 次下载
- 2.3.1 乘方 第2课时 有理数的混合运算(教学设计) --2024--2025学年人教版(2024)七年级数学上册 教案 3 次下载
- 2.3.2 科学记数法(教学设计) --2024--2025学年人教版(2024)七年级数学上册 教案 3 次下载
- 2.3.3 近似数(教学设计) --2024--2025学年人教版(2024)七年级数学上册 教案 3 次下载
人教版(2024)七年级上册(2024)2.3 有理数的乘方第1课时教案
展开第1课时 有理数的乘方
解题大招一 利用偶次幂的非负性解决问题
(1)一个数的偶次幂和绝对值都是非负数.
(2)若几个非负数的和为0,则每个非负数都是0.
(3)若一个数的正整数次幂为0,则这个数为0.
例1 (1)若(x-4)2+|y+1|=0,则x的值为4,y的值为-1.
(2)如果(a+3)2+|b-2|=0,那么(a+b)2 025=-1.
解析:(1)因为(x-4)2+|y+1|=0,(x-4)2是非负数,|y+1|是非负数,所以(x-4)2=|y+1|=0,所以x=4,y=-1.
(2)因为(a+3)2+|b-2|=0,(a+3)2是非负数,|b-2|是非负数,所以(a+3)2=|b-2|=0,所以a=-3,b=2.所以(a+b)2 025=[(-3)+2]2 025=(-1)2 025=-1.
解题大招二 互为相反数的两个数的幂与几个特殊值的幂
例2 (1)下列各组数中,互为相反数的有( B )
①(-3)3和33;②(-1)4和-14;③23和32;④(-2)3和-23.
A.④ B.①② C.①②③ D.①②④
(2)计算:(-1)2n+(-1)2n+1= 0 (n为正整数).
培优点 有理数乘方的应用
例 一根1 m长的铜丝,第一次剪去铜丝的 eq \f(1,4) ,第二次剪去剩下铜丝的 eq \f(1,4) ,如此剪下去,第2 025次剪完后剩下铜丝的长度是( C
A.( eq \f(1,4) )2 025m B.( eq \f(1,4) )2 024m C.( eq \f(3,4) )2 025m D.( eq \f(3,4) )2 024m
解析:第一次剪去铜丝的 eq \f(1,4) ,剩下铜丝的长度是1×(1- eq \f(1,4) )= eq \f(3,4) m,第二次剪去剩下铜丝的 eq \f(1,4) ,剩下铜丝的长度是 eq \f(3,4) ×(1- eq \f(1,4) )=( eq \f(3,4) )2,……,依次类推,第2 025次剪完后剩下铜丝的长度是( eq \f(3,4) )2 025m.故答案为C.
教学目标
课题
2.3.1 第1课时 有理数的乘方
授课人
素养目标
1.理解有理数乘方的意义,知道幂、底数、指数的概念.
2.已知一个数,会求它的乘方,提高运算能力.
3.知道有理数乘方的符号规律.
4.会利用计算器进行乘方运算,进一步提高运用计算工具的能力.
教学重点
幂、底数、指数的概念及其表示,理解有理数乘法运算与乘方间的联系,处理好负数的乘方运算.
教学难点
准确理解底数、指数和幂三个概念,并能求负数的正整数次幂.
教学活动
教学步骤
师生活动
活动一:创设情境,导入新课
【情境导入】
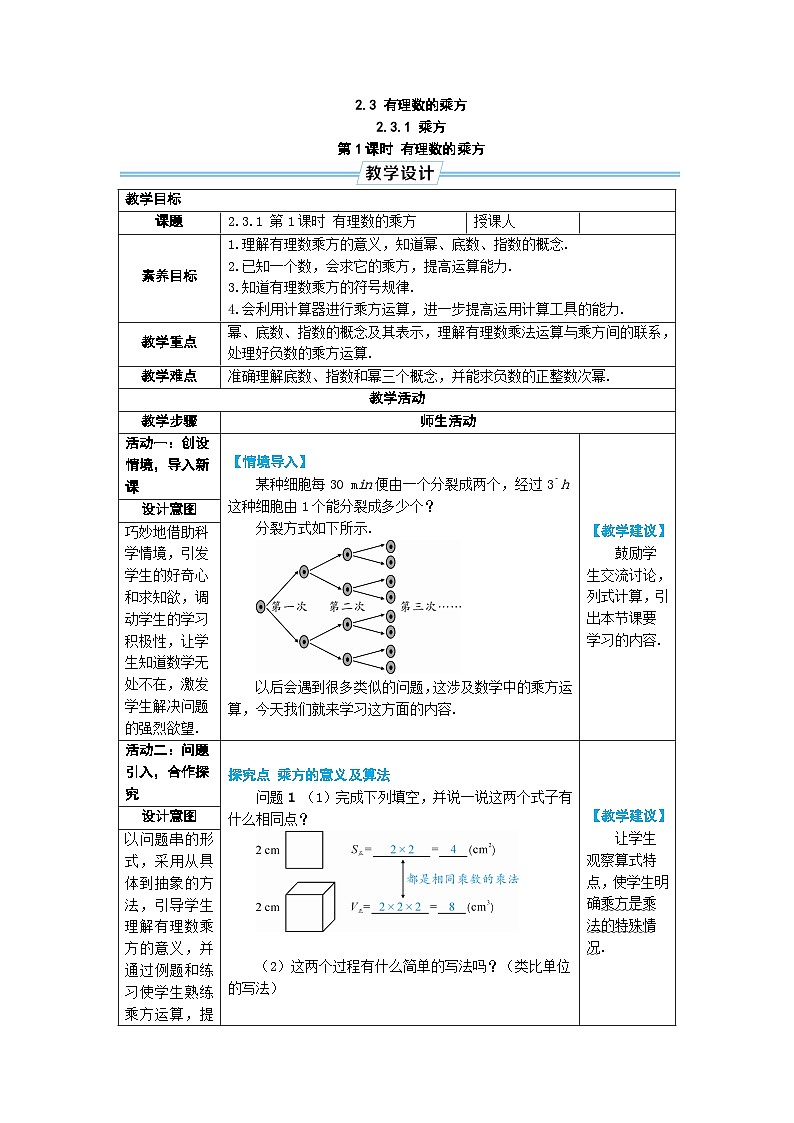
某种细胞每30 min便由一个分裂成两个,经过3`h这种细胞由1个能分裂成多少个?
分裂方式如下所示.
以后会遇到很多类似的问题,这涉及数学中的乘方运算,今天我们就来学习这方面的内容.
【教学建议】
鼓励学生交流讨论,列式计算,引出本节课要学习的内容.
设计意图
巧妙地借助科学情境,引发学生的好奇心和求知欲,调动学生的学习积极性,让学生知道数学无处不在,激发学生解决问题的强烈欲望.
活动二:问题引入,合作探究
探究点 乘方的意义及算法
问题1 (1)完成下列填空,并说一说这两个式子有什么相同点?
(2)这两个过程有什么简单的写法吗?(类比单位的写法)
【教学建议】
让学生观察算式特点,使学生明确乘方是乘法的特殊情况.
设计意图
以问题串的形式,采用从具体到抽象的方法,引导学生理解有理数乘方的意义,并通过例题和练习使学生熟练乘方运算,提高运算能力.
教学步骤
师生活动
问题2 类比以上研究,填写下面的表格:
(-2)×(-2)×(-2)×(-2)
(-2)4
-2的4次方
(- eq \f(2,5) )×(- eq \f(2,5) )×(- eq \f(2,5) )×(- eq \f(2,5) )×(- eq \f(2,5) )
(- eq \f(2,5) )5
- eq \f(2,5) 的5次方
【教学建议】
教师酌情解释中“…”再加上“n个”的标示,整体表示“n个a相乘”.
【教学建议】
提醒学生:乘方是一种运算,幂是乘方的结果.
【教学建议】
对于一个数的情况,可给学生提供一种角度:指数就是指相同乘数的个数,指数是1,就是指只有一个乘数.这种规定可为以后整式次数的讲解做铺垫.
【教学建议】
引导学生用多个有理数相乘的符号法则来发现负数的幂的符号规律,用有理数的乘法法则得出正数和0的幂的符号规律,最后总结出有理数乘方的符号规律.
问题3 (-2)4与-24一样吗?为什么?
不一样,(-2)4表示-2的4次方,-(2×2×2×2)记作-24,-24表示2的4次方的相反数.
一般地,n个相同的乘数a相乘,即,记作an,读作“a的n次方”.
概念引入:
求n个相同乘数的积的运算,叫作乘方,乘方的结果叫作幂.在an中,a叫作底数,n叫作指数.当an看作a的n次方的结果时,也可读作“a的n次幂”.
试一试:填一填下面图示中的空.
注意:一个数可以看作这个数本身的1次方.例如,5就是51.指数1通常省略不写.
例1 (教材P51例1) 计算:
(1)(-4)3; (2)(-2)4; (3)(- eq \f(2,3) )3.
解:(1)(-4)3=(-4)×(-4)×(-4)=-64;
(2)(-2)4=(-2)×(-2)×(-2)×(-2)=16;
(3)(- eq \f(2,3) )3=(- eq \f(2,3) )×(- eq \f(2,3) )×(- eq \f(2,3) )=- eq \f(8,27) .
例1变式 计算:
(1)(-1)5; (2)(-0.5)2; (3)(- eq \f(1,3) )4.
解:(1)(-1)5=(-1)×(-1)×(-1)×(-1)×(-1)=-1;
(2)(-0.5)2=(-0.5)×(-0.5)=0.25;
(3)(- eq \f(1,3) )4=(- eq \f(1,3) )×(- eq \f(1,3) )×(- eq \f(1,3) )×(- eq \f(1,3) )= eq \f(1,81) .
思考:(1)结合例1和例1变式,你发现负数的幂的正负与指数有什么关系?
当指数是奇数时,负数的幂是负数;
当指数是偶数时,负数的幂是正数.
教学步骤
师生活动
设计意图
(2)如果幂的底数是正数,那么这个幂有可能是负数吗?
不可能,正数的任何次幂都是正数.
归纳总结:
根据有理数的乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数;
正数的任何次幂都是正数,0的任何正整数次幂都是0.
例2 (教材P52例2) 用计算器计算(-8)5和(-3)6.
解:用带符号键的计算器,有
显示结果为-32768;
显示结果为729.
因此,(-8)5=-32`768,(-3)6=729.
【对应训练】
教材P52练习.,
让学生了解如何用计算器进行乘方运算,进一步培养学生使用计算工具的意识与能力.
活动三:知识延伸,巩固升华
例3 计算:
(1)-(- eq \f(3,2) )2; (2)-(-3)3;
(3)-(-1A eq \f(1,4) )3; (4)(-4)2×(-2)3.
解:(1)-(- eq \f(3,2) )2=-[(- eq \f(3,2) )×(- eq \f(3,2) )]=- eq \f(9,4) ;
(2)-(-3)3=-[(-3)×(-3)×(-3)]=-(-27)=27;
(3)-(-1 eq \f(1,4) )3=-[(- eq \f(5,4) )×(- eq \f(5,4) )×(- eq \f(5,4) )]=-(- eq \f(125,64) )= eq \f(125,64) ;
(4)(-4)2×(-2)3=16×(-8)=-128.
【对应训练】
计算:(1)-(- eq \f(2,7) )2;(2)-(-6)3;
(3)-(-1 eq \f(1,3) )4;(4)(-22)×(-3)3.
解:(1)-(- eq \f(2,7) )2=-[(- eq \f(2,7) )×(- eq \f(2,7) )]=- eq \f(4,49) ;
(2)-(-6)3=-[(-6)×(-6)×(-6)]=-(-216)=216;
(3)-(-1A eq \f(1,3) )4=-[(- eq \f(4,3) )×(- eq \f(4,3) )×(- eq \f(4,3) )×(- eq \f(4,3) )]=- eq \f(256,81) ;
(4)(-22)×(-3)3=(-4)×(-27)=108.
【教学建议】
选取学生代表上台板演,其他学生在纸上作答,提醒学生:(1)底数是带分数时可先将带分数化成假分数再计算;(2)对于例3(4)和对应训练的第(4)问,可将幂看作单独的一个数,先算出幂后再来计算乘法.
设计意图
通过例题和练习帮助学生进一步掌握乘方运算,熟悉负数的幂的符号规律,并为后续的混合运算做铺垫.
活动四:【随堂训练】,【课堂总结】
【课堂总结】 师生一起回顾本节课所学主要内容,并请学生回答以下问题:
1.什么是乘方?在乘方中,幂、底数、指数分别指的是什么?
2.怎样计算一个有理数的乘方?
3.有理数的乘方的符号规律是怎样的?
【知识结构】
【作业布置】
1.教材P56习题2.3第1,2,7,11,12题.
教学步骤
师生活动
板书设计
2.3 有理数的乘方
2.3.1 乘方
第1课时 有理数的乘方
1.乘方的意义及相关概念 2.有理数乘方的计算
3.有理数乘方的符号规律
教学反思
本节课从一个科学情境出发,激发学生学习兴趣,通过具体的例子,逐步引入乘方的概念,使学生体会到乘方与乘法的关系,进而理解乘方运算,同时体会幂、底数、指数之间的关系.接着通过例题和练习进一步理解乘方的意义,并归纳总结有理数乘方的符号规律,掌握乘方运算,提高推理能力和运算能力.同时学习用计算器计算乘方的操作,进一步培养学生利用计算工具的意识和能力.然后巩固加强学生对于负数的幂的符号规律的理解,并为后续的混合运算做一点铺垫,整体效果较好.
互为相反数的两个数的幂
①互为相反数的两个数的奇次幂仍互为相反数,即-am=(-a)m(m为奇数);
②互为相反数的两个数的偶次幂相等,即an=(-a)n(n为偶数)
几个特殊值的幂
①0的任何正整数次幂都是0;②1的任何正整数次幂都是1;③-1的奇次幂都是-1,-1的偶次幂都是1
注意
如果一个数的偶次幂是正数,那么这个幂的底数有两个,且互为相反数
人教版(2024)七年级上册(2024)2.3 有理数的乘方第2课时教案设计: 这是一份人教版(2024)七年级上册(2024)<a href="/sx/tb_c4050859_t8/?tag_id=27" target="_blank">2.3 有理数的乘方第2课时教案设计</a>,共8页。教案主要包含了教学目标,课型,课时,教学重难点,课前准备,教学过程,课后作业,板书设计等内容,欢迎下载使用。
数学人教版(2024)2.3 有理数的乘方教案设计: 这是一份数学人教版(2024)<a href="/sx/tb_c4050859_t8/?tag_id=27" target="_blank">2.3 有理数的乘方教案设计</a>,共7页。
初中数学人教版(2024)七年级上册(2024)第二章 有理数的运算2.3 有理数的乘方第2课时教学设计: 这是一份初中数学人教版(2024)七年级上册(2024)<a href="/sx/tb_c4050859_t8/?tag_id=27" target="_blank">第二章 有理数的运算2.3 有理数的乘方第2课时教学设计</a>,共4页。













