第23章 旋转复习小结 第2课时 旋转模型-2024-2025学年九年级数学上册教材配套同步课件（人教版）

这是一份第23章 旋转复习小结 第2课时 旋转模型-2024-2025学年九年级数学上册教材配套同步课件（人教版），共26页。

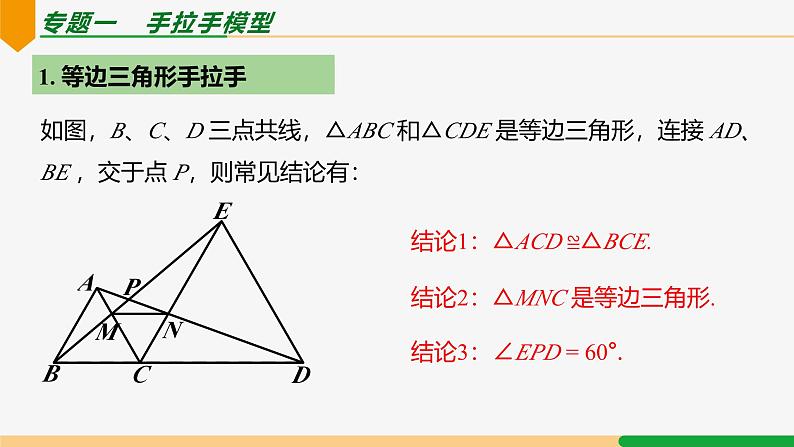
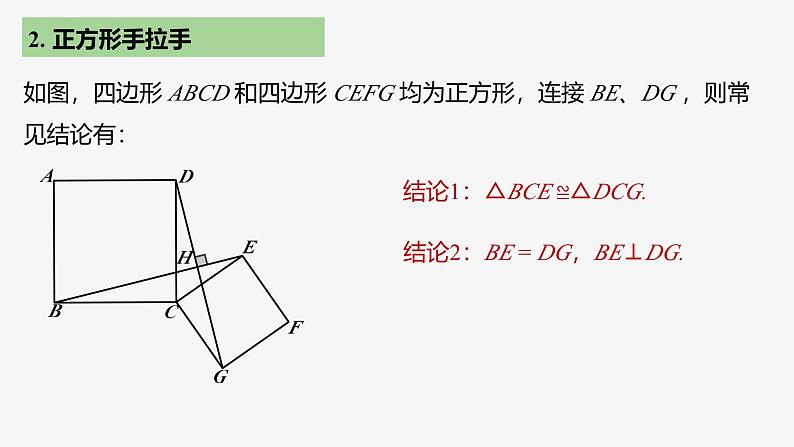
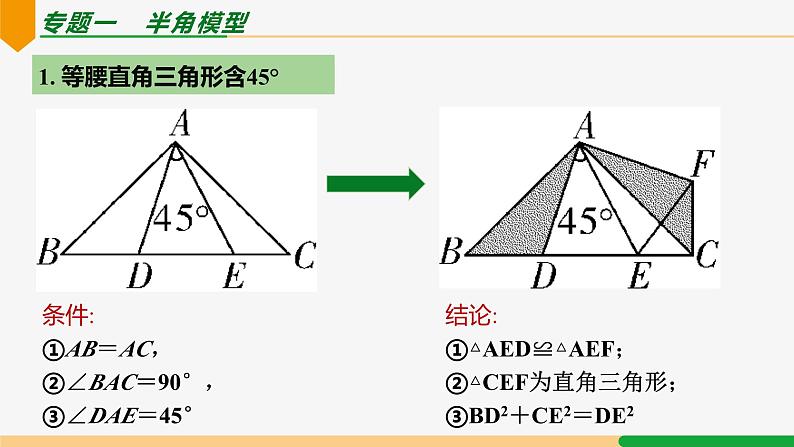
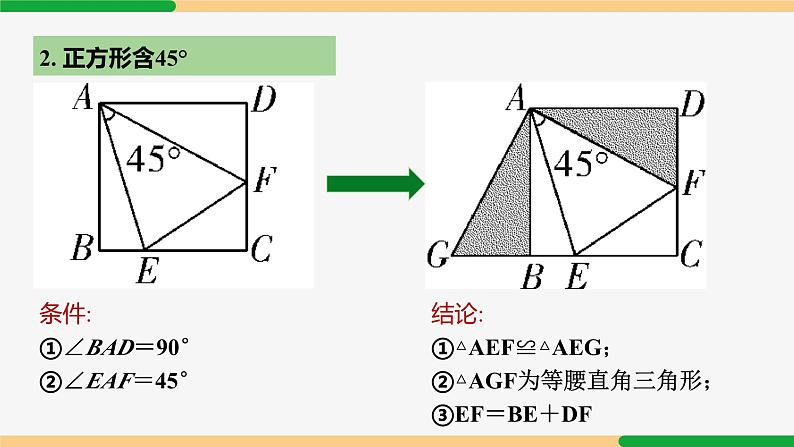
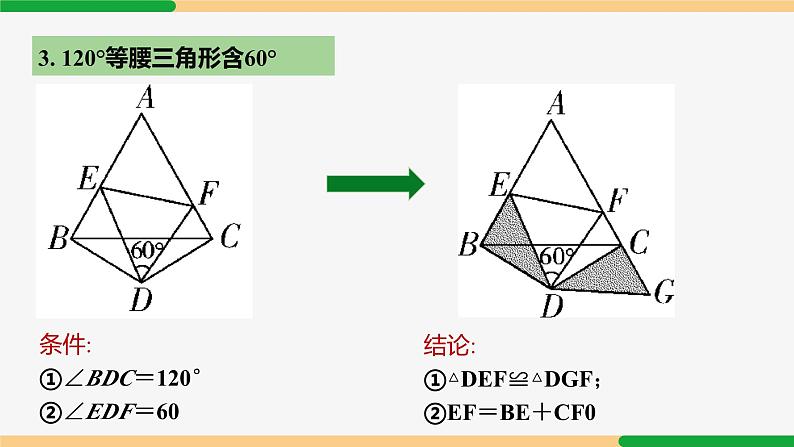
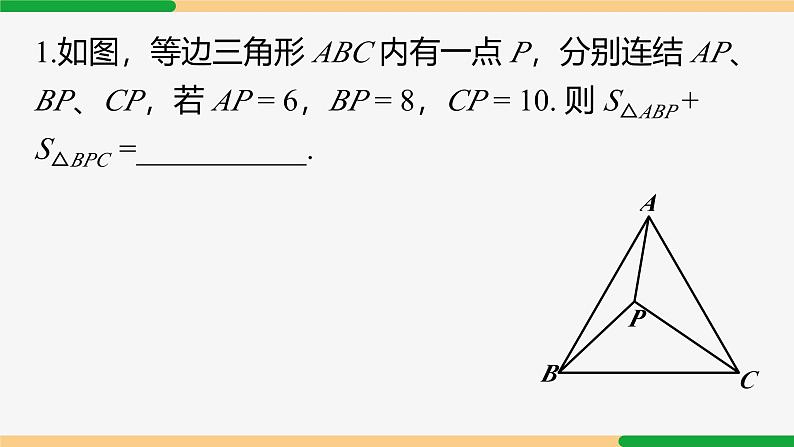
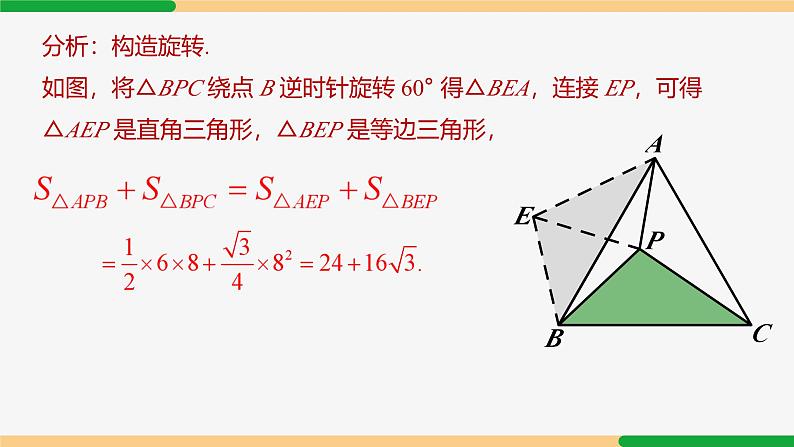
旋转模型第23章 旋转复习和小结| 第2课时|专题一 手拉手模型1. 等边三角形手拉手 如图，B、C、D 三点共线，△ABC 和△CDE 是等边三角形，连接 AD、 BE ，交于点 P，则常见结论有：结论1：△ACD ≌△BCE.结论2：△MNC 是等边三角形.结论3：∠EPD = 60°.2. 正方形手拉手 如图，四边形 ABCD 和四边形 CEFG 均为正方形，连接 BE、DG ，则常见结论有：结论1：△BCE ≌△DCG.结论2：BE = DG，BE⊥DG.专题一 半角模型1. 等腰直角三角形含45° 条件:①AB＝AC，②∠BAC＝90°，③∠DAE＝45°结论:①△AED≌△AEF；②△CEF为直角三角形；③BD2＋CE2＝DE22. 正方形含45° 条件:①∠BAD＝90°②∠EAF＝45°结论:①△AEF≌△AEG；②△AGF为等腰直角三角形；③EF＝BE＋DF3. 120°等腰三角形含60° 条件:①∠BDC＝120°②∠EDF＝60结论:①△DEF≌△DGF；②EF＝BE＋CF01.如图，等边三角形 ABC 内有一点 P，分别连结 AP、BP、CP，若 AP = 6，BP = 8，CP = 10. 则 S△ABP + S△BPC =___________.分析：构造旋转.如图，将△BPC 绕点 B 逆时针旋转 60° 得△BEA，连接 EP，可得△AEP 是直角三角形，△BEP 是等边三角形，2. 如图，正方形 ABCD 和正方形 CEFG 边长分别为 a 和 b，正方形 CEFG 绕点 C 旋转，给出下列结论：① BE = DG；② BE⊥DG；③ DE² + BG² = 2a² + 2b²，其中正确结论是__________(填序号).分析：①②显然正确，下分析③：连接 BD、EG、DE，BD² + EG² = 2a2 +2b2，记 BE、DG 交点为 H 点，BD² = BH² + DH²，EG2 = EH² + GH²，DE² = DH² + EH²，BG2 = BH² + GH2，∴ DE² + BG² = BD² + EG².∴ DE² + BG2 = 2a2 +2b2.故正确的结论有①②③.例1 如图，在四边形 ABDC 中，AB＝3，AC＝2，将△ABD 绕点 D 顺时针方向旋转 60° 后得到△ECD，此时发现点 A、C、E 恰好在一条直线上，求∠BAD的度数与 AD 的长.∵ 点 A、C、E 在一条直线上，∴△ADE 为等边三角形.∴ AD＝AE，由旋转得∠BAD＝∠E＝60°. 由旋转，CE＝AB＝3.∴ AE＝AC＋CE＝2＋3＝5， ∴ AD＝5. 3. 如图，在△ABC 中，∠ABC＝30°，AB＝6，BC＝8，△ACD 是等边三角形，求 BD 的长. 解：将△ABD 绕点 A 顺时针旋转 60°，得△AEC，连接 BE，则 AB＝AE，∠BAE＝60°，得等边△ABE，∴∠ABE＝60°，BE＝AB＝6. ∠EBC＝60°＋30°＝90°.由旋转得 BD＝CE＝10. [解题策略] 共顶点的等腰三角形→旋转→全等 旋转60°(补形)→构造共顶点的两个等边三角形  ∴ AQ＝PA＝1，∠QAP＝∠CAB＝90°，(2) ∵ AQ＝AP，∠PAQ＝90°，∴∠APQ＝45°.∵△APB 绕点 A 逆时针旋转后与△AQC 重合，∴CQ＝PB＝3.∴ PC2＋PQ2＝CQ2. ∴∠CPQ＝90°.∴ ∠APC＝∠APQ＋∠CPQ＝45°＋90°＝135°.解：(1)∵△APB 绕点 A 逆时针旋转后与△AQC 重合，解：将△ABD 绕点 A 顺时针旋转 90° 得△AEC，连接 BE，则△ABE 为等腰直角三角形，∵∠ABC＝45°，∴∠EBC＝45°＋45°＝90°.由旋转，得 BD＝CE＝13. [解题策略] 共顶点的等腰三角形→旋转→全等 旋转90°(补形)→构造共顶点的两个等边三角形 解：将线段 AP 绕点 A 顺时针旋转 120° 得线段 AQ，连接 PQ、BQ，∴∠APQ＝45°.则在△APQ 中，AP＝AQ，∠PAQ＝120°，∵∠BAC＝∠PAQ＝120°，∴∠BAQ＝∠CAP. 在△ABQ 和△ACP 中，∵AB＝AC，∠BAQ＝∠CAP，AQ＝AP，∴△ABQ≌△ACP(SAS).∴∠AQB＝∠APC. 设∠AQB＝∠APC＝α，∵∠APC+∠BPC＝90°，∴∠BPC＝90°－α，则∠APB＝90°－2α.∴∠BPQ＝∠APB＋∠APQ＝90°－2α＋30°＝120°－2α.又∠PQB＝∠AQB＋∠AQP＝α＋30°，∴∠PBQ＝180°－(120°－2α)－(α＋30°)＝α＋30°.∴∠PQB＝∠PBQ. ∴ BP＝PQ＝ AP.[解题策略] 共顶点的等腰三角形→旋转→全等 旋转120°(补形)→构造共顶点的两个等边三角形 例4 如图，五边形 ABCDE 中，∠BCD＝∠BAE＝90°， BC＝CD，AB＝AE，M 为 DE 上一点，∠MAC＝45°. 求证：DM＝EM. 解：∵ BC＝CD，∠BCD＝90°，故将△CAB 绕点 C 顺时针旋转 90°，得△CHD，连接 AH，则 CH＝CA，CH⊥CA，△ACH 为等腰直角三角形.∴∠CAH＝45°.又∵∠MAC＝45°，∴点 M 在线段 AH 上. 在五边形 ABCDE 中，∠BCD＝∠BAE＝90°，∴∠CDE＋∠B＋∠E＝540°－2×90°＝360°，又∠CDH＋∠CDE＋∠EDH＝360°.由旋转得∠CDH＝∠B，∴∠EDH＝∠E.∵ DH＝AB＝AE，∴△DMH≌△EMA(AAS).∴ DM＝EM. [解题策略] 共顶点的等腰三角形→旋转→全等 在 90° 内套45° → 旋转90°  解：(1) 如图，△ACK 为所求.(2) 连接 KE，过 K 作 KQ⊥AC 于 Q，由旋转得 BF＝AK，CF＝CK，∠KCF＝∠ACB＝120°. ∵∠ECF＝60°，∴∠ECK＝60°＝∠ECF. ∴△ECF≌△ECK(SAS).∴ EF＝EK，∠CEF＝∠CEK. 又∵AE2＋EF2＝BF2，∴AE2＋EK2＝AK2，由勾股定理的逆定理，得∠AEK＝90°，∴∠KEF＝90°，∴∠CEF＝∠CEK＝45°，∠AEC＝135°. 又∵∠CAE＝30°，∴∠ACE＝15°.∴∠ACK＝60°－15°＝45°，△CKQ 为等腰直角三角形.由旋转得∠CAK＝∠B＝30°，∴BF＝AK＝2KQ. [解题策略] 共顶点的等腰三角形→旋转→全等 在 120° 内套 60° → 旋转120°